Tangency Portfolio

Publication Date :

15 Jun, 2025

Blog Author :

Edited by :

Reviewed by :

Table of Contents

What Is Tangency Portfolio?

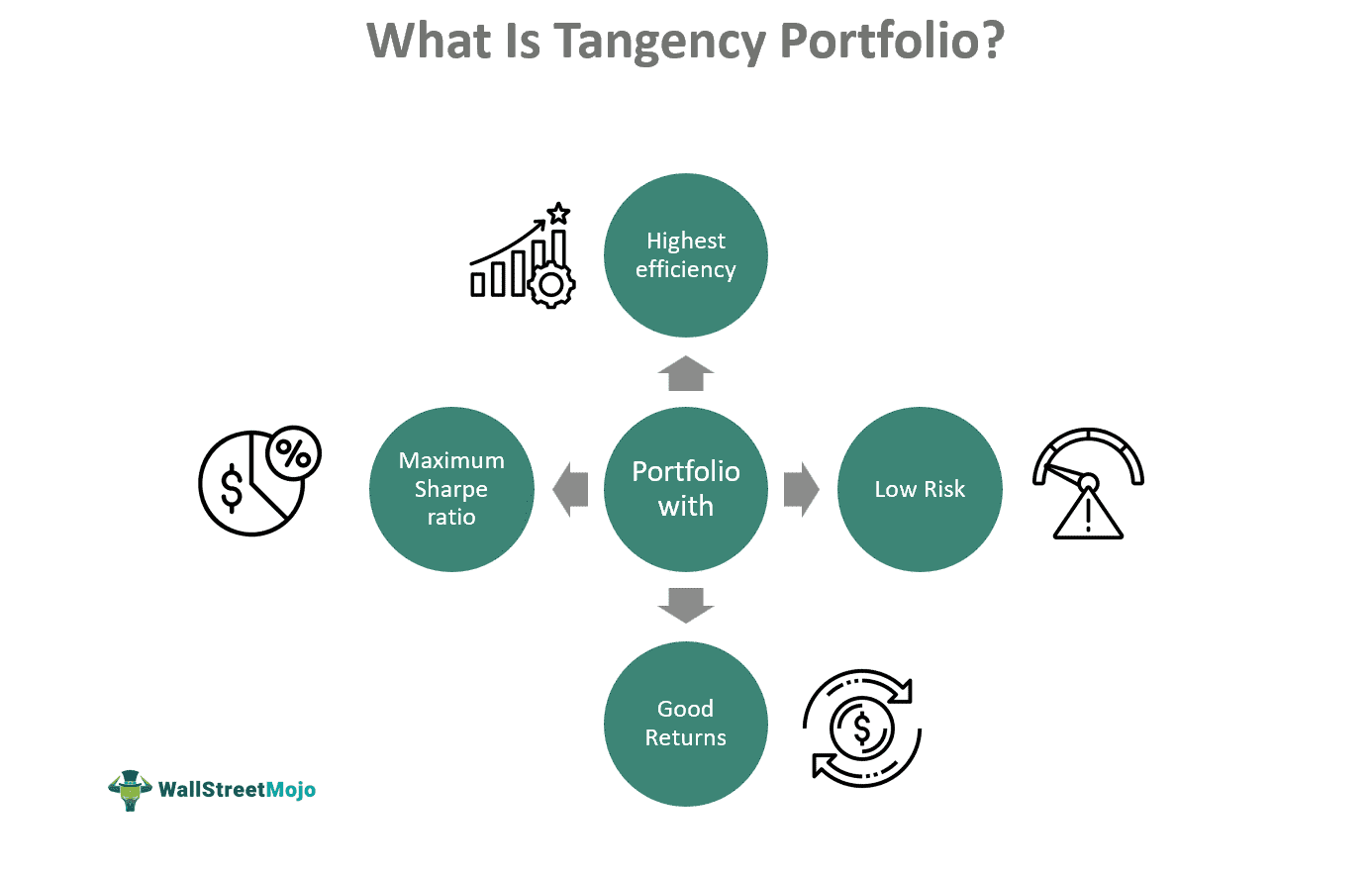
The tangency portfolio definition is stated as a portfolio that has the highest efficiency, lowest risk, and excellent returns due to the maximum Sharpe ratio. One can easily combine cash and this portfolio to create the best portfolio with a designated risk tolerance.

In other words, the tangency portfolio gets at most that of the market portfolio. Every investor must necessarily have this portfolio T for investments. Investors must only demand a mix of T portfolio and risk-free assets. It makes up the demand side of the market. Now, the supply side of the markets comprises all the assets existing in the market.

Key Takeaways

A tangency portfolio is understood as that point where both the lines – optimum returns line and capital market line, tend to touch each other, giving the best efficient portfolio.
It helps the traders choose the most profitable and least risky portfolio of security by mixing it with cash to get any risk portfolio to deal with any risk tolerance level.
Furthermore, the assets' weight plus total market capitalization must be proportionately equal within the market portfolio.

Tangency Portfolio Explained

A tangency portfolio is a portfolio where the capital market line intersects the efficient frontier. It is known as the best form of the portfolio, having the perfect balance of maximum returns at minimal risk. Moreover, the efficient frontier can be understood as that line that gives the best-yielding portfolios for the given level of risk. Also, any portfolio that lies above the efficient frontier line gives not only a portfolio of high return but also the risk involved assumes a higher value than the given risk rate.

One can also take this portfolio as the optimal portfolio of all the risky assets called the market portfolio. Traders get to invest all their investable funds and more into the risky market portfolio by funds borrowers at a risk-free rate. As a result, the traders or investors get ways to increase their expected return as well as the risk that is offered by the market portfolio.

Furthermore, as everyone knows, for equilibrium to take place, demand must be equal to supply. Therefore, the assets picked up in the market portfolio have to be equal in number to that of all assets present in the market. Moreover, the supply side of the asset is represented by its market capitalization. Therefore, to achieve equilibrium of assets, one has to have the assets in the tangency portfolio to be in the same proportion as that of their market capitalization. Finally, the tangency portfolio in r must have assets weight and overall market capitalization in equal percentages.

Formula

The tangency portfolio is termed as that portfolio that has risky assets with the highest Sharpe ratio. Here, the tangency portfolio gets denoted as

t=(t1,…,tN)′t=(t1,…,tN)′,

Resolves the problem of constrained maximization:

max(t) t′μ−rf/(t′Σt)^1/2

=μp, t−rfσp, t s.t. t′1=1 ……………………………..(1)

where μp, t=t′μμp, t=t′μ

and σp, t=(t′Σt)12σp,t=(t′Σt)12.

The Lagrangian for such a problem has been:

L(t, λ)=(t′μ−rf)(t′Σt)−12+λ(t′1−1).

Using the rule of chain, the 1st order conditions get as. ∂L(t,λ)/∂t=μ(t′Σt)−1/2−(t′μ−rf)(t′Σt)−3/2Σt+λ1=0

, ∂L (t,λ)/∂λ=t′1−1=0.

After a lot of complex algebraic calculations, one can see that the solution for

Tangency portfolio, t, can be expressed simply as t=Σ−1(μ−rf⋅1)/1′Σ−1(μ−rf⋅1)……………( 2 )

Alternatively, one can derive the formula as

T max slope = μp-rf/ σp that gets subjected to μp = t’μ

σp = (t’Σt)1/2

& t’1 = 1,

Where μp = portfolio return, σp = standard deviation

t = vector portfolio weights

μ = vector expected returns &

Σ = covariance matrix of the returns

Calculation Example

Let us look at an example to learn more about the topic. Let us assume that:

Wa = security 1 within tangency portfolio weights

Wb = security 2 within tangency portfolio weights

However, Wa + Wb = 1

Therefore, Wb= 1- Wa

Hence, the portfolios mean return:

= Wa*(security 1’s mean return) + Wb*(security 2’s mean return)

= 2Wa + Wb

= 1 + Wa

Plus,

Return of portfolio's variance:

= (Wa^2)*(return of security 1’s Variance) + (Wb^2)*(return of security 2’s Variance) + 2*Wa*Wb*(return of security 1’s & return of security 2’s Covariance)

= 4(Wa ^2) + 1(Wb^2) + 2*(Wa*Wb)*2p

= 4(Wa ^2) + (1+Wa^2–2Wa) + 2*(Wa-Wa^2)*2p

= (5–4p) *Wa^2 + (4p-2)*Wa+ 1

To maximize utility,

Utility of portfolio’s derivative with respect to Wa =0

Moreover, as already defined in the given problem,

Portfolio’s Utility

= return of portfolio’s Mean - (b/2) *(return of portfolio’s Variance)

Therefore,

Utility of portfolio’s Derivative with respect to Wa

= Mean return of portfolio’s derivative with respect to Wa - (b/2)*(Variance of return of portfolio’s derivative with respect to Wa)

= 0