Branch and Bound

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

Branch and bound, or BnB, is an algorithm design paradigm that solves combinatorial and discrete optimization problems. Many optimization issues, such as crew scheduling, network flow problems, and production planning, cannot be solved in polynomial time. Hence, BnB is a paradigm that is widely used to solve such problems.

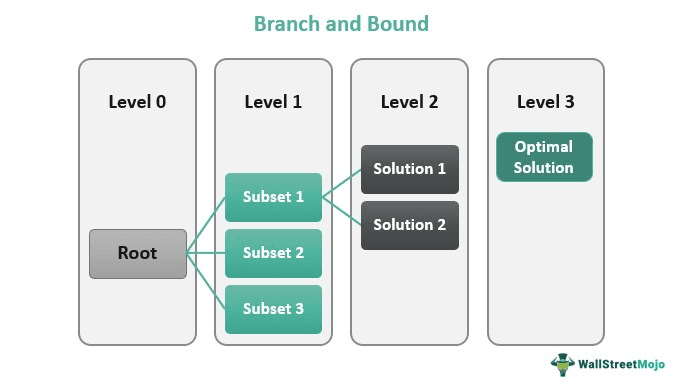
This algorithm heavily depends on efficiently estimating the search space's lower and upper limits of branches. It degenerates to an exhaustive or thoroughgoing search if no limits are found. The branch and bound method solves these complex problems relatively faster. In most discrete optimization problems, the BnB method is a reliable choice to solve the issue.

What is Branch and Bound?

The branch and bound algorithm solves an optimization problem with time complexity.
It was introduced in 1960 by two researchers, Alisa Land and Alison Diog, from the London School of Economics.
The algorithm divides a big optimization problem into smaller and simpler subsets and scans for the best possible solution among the candidate solutions.
The algorithm searches the tree entirely before arriving at the best solution. This process is considered to be a time-consuming process, especially for big or complex problems.

Branch And Bound Algorithm Explained

Branch and bound is an algorithm used to solve combinatorial optimization problems. These problems are usually augmented in terms of time complexity and issues that require exploring all permutations and combinations possible in a worst-case scenario.

The branch and bound calculator is typically used to solve problems that are not solvable in polynomial time, such as network flow issues, crew scheduling, and production planning. However, it can be better understood as a backtracking tool using the state space tree.

As the name suggests, BnB explores branches or nodes under a particular subset of solutions. The parent node is considered to have all the possible solutions to the said problem. However, before the candidate solutions to the issue are computed or enumerated, the upper and lower limit binds the optimal solution.

The branch and bound method were put forth first by Alisa Land and Alison Doig from the London School of Economics in 1960 as a discrete programming solution. However, the name "BnB" was first used officially in a study on traveling salesman issues.

Applications

The BnB algorithm is an excellent addition to an organization’s problem-solving armory, especially when branch and bound notes all possibilities in the worst-case scenario. Furthermore, it is applied in situations where a combination of tasks is to be optimized. Let us discuss a few cases where BnB would be a good choice:

Discrete Optimization: Discrete optimization is a subset of optimization where the variables of a particular problem must belong to a discrete set, for example, network flow issues. In situations like these, the BnB algorithm is a sensible choice.
Combinatory Optimization: Since it is established that an optimization problem is to be solved, combinatory optimization finds the maximum and minimum bounds of the given function. The domain of the process must be discrete or unattached and significant.

Advantages And Disadvantages

Let us understand the advantages and disadvantages of BnB through the points below:

Advantages

Time Complexity: The BnB algorithm does not explore all nodes in the tree. Thereby, the time complexity is significantly lesser than most other algorithms.
Optimal Solution: If the branching is done reasonably, the algorithm can find the optimal solution in a reasonable period.
Clear Pattern: The BnB algorithm does not repeat the notes to explore the tree for the candidate solutions; instead, it follows a minimal path to derive the optimal solution.

Disadvantages

Time-consuming: Based on the size of the problem, the number of nodes that are computed might be too large in a worst-case scenario, making it a time-consuming process.
Parallelization: The branching out of possible solutions provides scope for speculative parallelism. However, when alternative actions are considered for the said action, the branch and bound calculator finds difficulty.

Difference Between Branch And Bound And Backtracking

Let us understand the difference between BnB and backtracking through the table below:

Basis	Branch and Bound	Backtracking
Basic Function	BnB is used to solve optimization issues.	Backtracking is used to find all solutions possible to a given problem
Approach	It can travel the tree in either DFS or Breadth First Search (BFS)	Based on the Depth First Search (DFS) approach
Additional Function	Involves bounding function	Involves feasibility function
Solution	The algorithm knows that it has a better optimal solution than the pre-solution. Hence, it abandons the pre-solution.	The system recognizes that it has made a wrong choice and undoes the last choice.
Search Spectrum	It searches the tree entirely before delivering the optimal solution	It explores the tree until the answer is found.

Branch And Bound vs Dynamic Programming

Even though BnB and dynamic programming solve optimization problems that ultimately lead to maximizing or minimizing the cost function of the given situation, they have a handful of differences. Let us understand them through the points below:

Branch And Bound

The BnB method solves mathematical optimization issues and discrete and combinatorial optimization problems.
Alisa Land and Alison Doig introduced it at the London School of Economics in 1960.
The solution is investigated in the branches or nodes of the tree.
Before candidate solutions are calculated, an upper and lower limit is set and tested to find the best possible solution.

Dynamic Programming

Dynamic programming is a mathematical optimization tool and a computer programming approach.
It was invented by Richard Bellman in the 1950s and has been used in various industries since then.
Dynamic programming breaks down a big problem into simpler and smaller subsets in the best and worst situations.
Since BnB can not deduce all situations or problems, data points are eliminated or dismantled in this manner.

Frequently Asked Questions ( FAQs)

1. How to solve branch and bound problems?

BnB problems are solved by segregating the solutions into subsets or smaller nodes in the solution tree that gives a detailed picture of all possible solutions. It is done after setting an upper and lower limit. It uses the lowest-cost branch, FIFO, or LIFO strategies to generate branch organizations.

2. How to use branch and bound method?

The BnB method is based on the ideology that the totality of candidate solutions can be divided into smaller solution nodes. After the divisions are made, the algorithm can systematically evaluate them until the best possible solution is found. This process takes significantly less time than other algorithms when carried out through BnB.

3. What is branch and the bound algorithm used for?

Typically, the BnB algorithm is used to solve combinatorial optimization issues. The nature of these problems usually are exponentially complex in terms of time and requires all possible permutations and combinations to be explored before arriving at the best possible solution.