SIN Excel Function

Last Updated :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

The SIN Excel function is a built-in trigonometric function in Excel that is used to calculate the sine value of a given number. Else, in terms of trigonometry, the sine value of a given angle, here the angle is a number in Excel. This function takes only a single argument which is the input number provided.

For example, we can use this function to convert 80° to radian. It will take 80° as 80.

=RADIANS(80) will give the radian 1.39.

SIN Function in Excel

The SIN function in Excel computes the sine of an angle we specify. It is categorized as a Math/Trigonometry function in Excel. It always returns a numeric value.

In mathematics and trigonometry, the SINE is a trigonometric function of an angle, which is a right-angled triangle is equal to the length of the opposite side (the right-angled side), divided by the length of the hypotenuse, and represented as:

Sin Θ = opposite side/ hypotenuse

Sin Θ = a/h

SIN Function in Excel

SIN Formula in Excel

Below is the SIN formula in Excel.

The number is an argument passed to the SIN formula in radians.

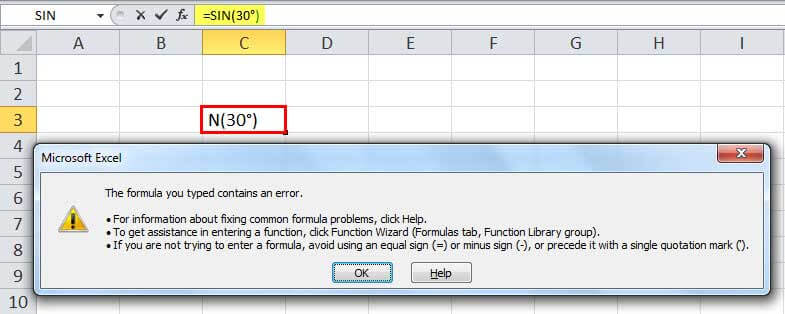
If we directly pass the angle to SIN in the Excel function, it will not recognize it as a valid argument. So, for example, if we give 30° as the argument to this SIN function in Excel, it will not recognize it as a valid argument. As a result, Excel will display an error message.

Hence, the argument that we need to pass must be in radians.

For converting an angle into a radian, there are two methods:

First, use the built-in Excel RADIANS function. The RADIANS function converts the degrees to a radian value.

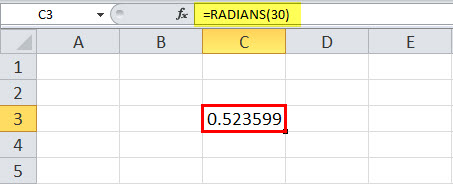
For example, we will use this function to convert 30° to radian. It takes the degree as a number. So it will be 30° as 30.

=RADIANS(30) will give the radian 0.52.

In the second case, we can use the mathematical formula for converting a degree to a radian. The formula is:

Radian = degrees * (π/180) (π =3.14)

Excel also has a function that returns the value of Pi, accurate to 15 digits, and the function is PI().

Therefore, for the degree to radian conversion, we would use the formula:

Radian = degrees * (PI()/180)

SIN Excel Function Video

How to Use SIN Function in Excel?

The SIN function in Excel is very simple and easy to use. Let us understand the working of SIN in Excel by some examples.

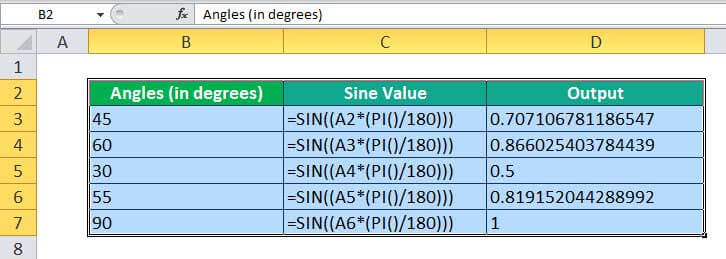
SIN in Excel Example #1

Calculating sine value using SIN function in Excel and RADIANS function in Excel

Calculating sine value using SIN function in Excel and PI function.

The sine function in Excel has many real-life applications. For example, it is widely used in architecture to calculate the heights and lengths of geometric figures. It is also used in GPS, optics, calculating trajectories, finding the shortest route based on latitude and longitude geographical location, radio broadcasting, etc. Even an electromagnetic wave is plotted as a sine and cosine function graph.

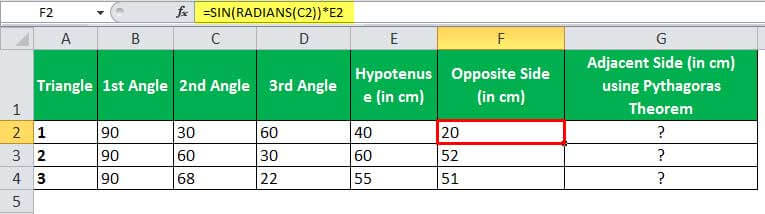
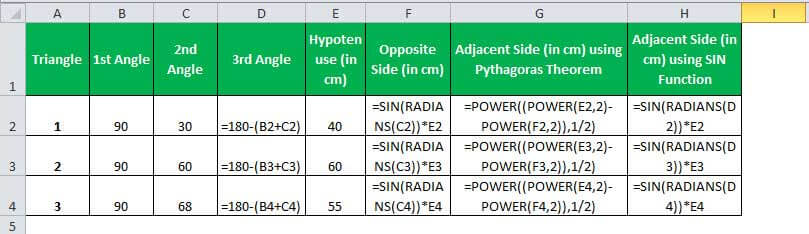
Suppose we have three right-angled triangles, given their angles and the length of one side. Next, we need to calculate the length of the other two sides.

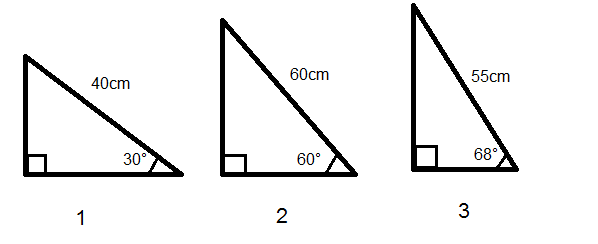
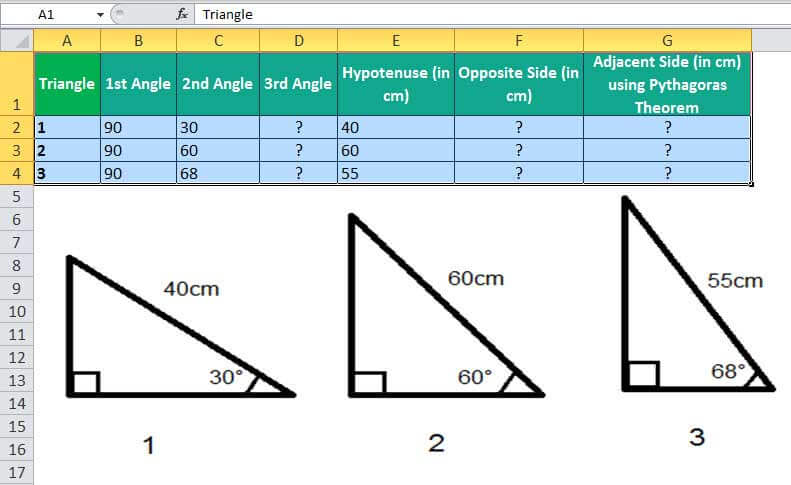
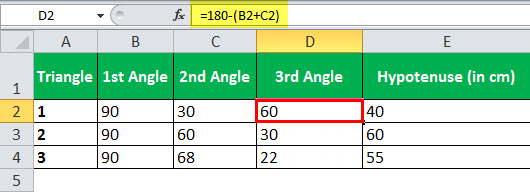
The sum of all the angles on a triangle is equal to 180°. Therefore, we can easily calculate the third angle.

We know, Sin Θ = opposite/hypotenuse

So, the opposite side length will be Sin Θ * hypotenuse

In Excel, the length of the opposite side (perpendicular side) will be calculated by the SIN formula:

=SIN(RADIANS(C2))*E2

Applying the above-given SIN formula for three triangles, we can get the length of perpendiculars of triangles.

We have two methods for the third side (adjacent side): using the Pythagoras theorem or using the SIN in Excel function from other angles.

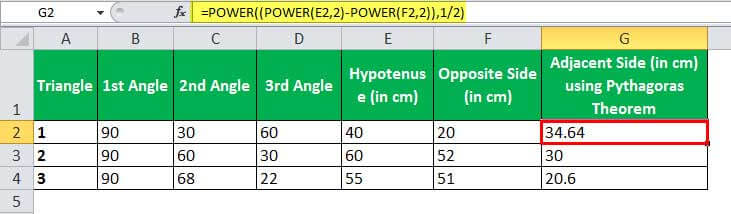
According to the Pythagoras theorem, the sum of squares of two sides of the right-angled triangle is equivalent to the square of the hypotenuse.

Hypotenuse²= Opposite²+ Adjacent²

Adjacent = (Hypotenuse² – Opposite²)^1/2

In Excel, we will write it as:

=POWER((POWER(Hypotenuse,2)-POWER(Opposite,2)),1/2)

Applying this formula, we compute the length of the adjacent side.

=POWER((POWER(E2,2)-POWER(F2,2)),1/2)

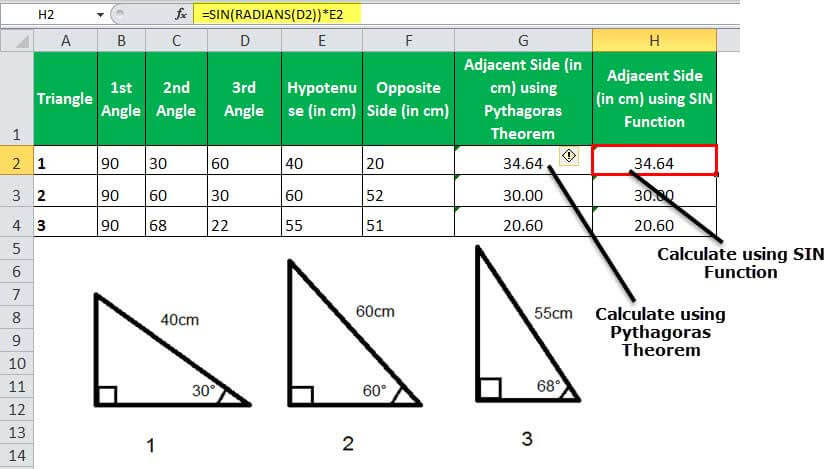
Using the second method, we can use the SINE of the third angle to calculate the value of the adjacent side.

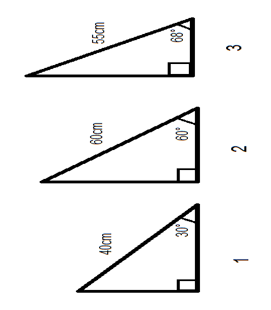
If we rotate the triangles to 90° left, the opposite side is swapped with the adjacent side, and the SIN of the angle between hypotenuse and adjacent will help calculate the value of the third side.

=SIN(RADIANS(D2))*E2

SIN in Excel Example #2

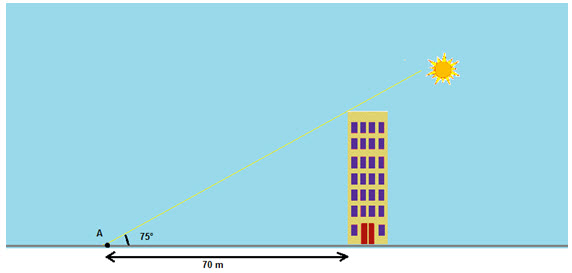
There is a tall building of unknown height, and sun rays at a point of making an angle at point A of 75°, thus creating a shadow of the building of 70 meters. Therefore, we need to find the height of the tower.

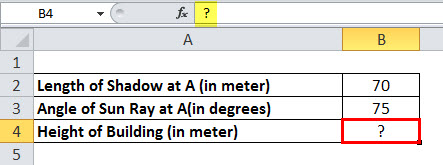
The height of the building will be calculated using the SIN in Excel function:

SIN 75° = Height of Building/ Length of Shadow at point A

Therefore, the height of the building = SIN 75° * Length of Shadow at point A

Hence, the height of the building will be:

=SIN(RADIANS(B3))*B2

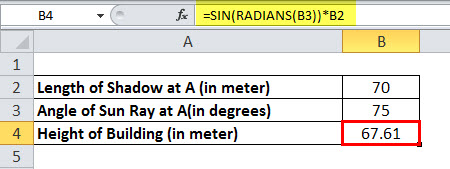
The height of the building is 67.61 meters.

SIN in Excel Example #3

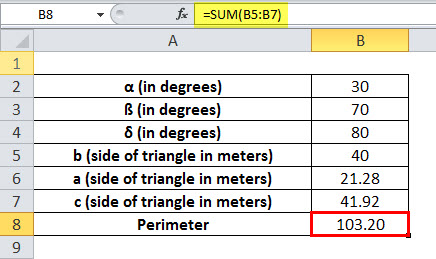
We have a land in the form of a triangle, for which the two angles are given as 30° and 70°, and we only know the length of one side of the triangle, which is 40 meters. Therefore, we need to find the length of the other three sides and the perimeter of the triangle.

For a triangle, when one side and all angles are known, we can calculate the other sides by SINE Rule

The sine rule in Trigonometry gives a relation of sin angles and sides of a triangle by a SIN formula:

a/sin α = b/sin ß = c/sin δ

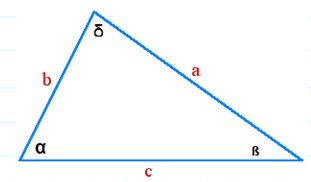
In this case,

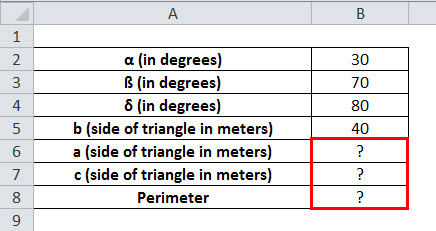
α = 30°, ß = 70° and δ = 180°-(30°+70°) = 80° and one side of triangle b = 40 meters

To find the other sides of the triangle, we will use the SINE rule.

a = Sin α * (b/sin ß)

Therefore,

a =SIN(RADIANS(30))*(B5/SIN(RADIANS(70)))

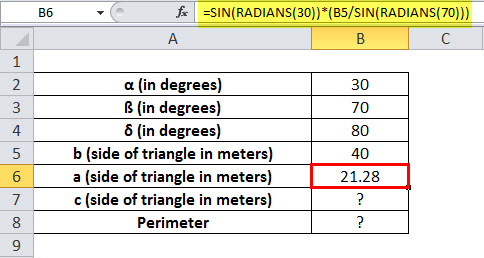
Length of side a = 21.28 meters

Similarly, the third side c will be

c = Sin δ * (b/sin ß)

Therefore,

c =SIN(RADIANS(80))*(B5/SIN(RADIANS(70)))

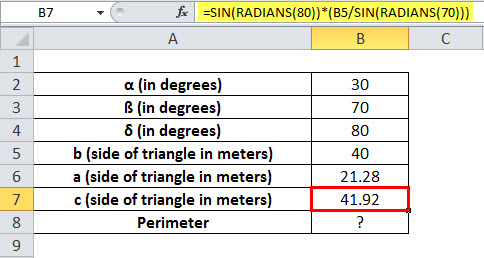
The triangle's three sides are 21.28, 40, and 41.92 meters.

The perimeter of the triangle is the sum of all the sides.

Therefore, the perimeter will be =SUM(B5:B7)