Factor Rotation

Factor rotation refers to a process of revolving the matrix in factor analysis to arrive at a clear, simple, interpretable, and meaningful data structure. This rotation of the axes representing the underlying factors emphasizes adjusting the loading of variables on the specific factors.

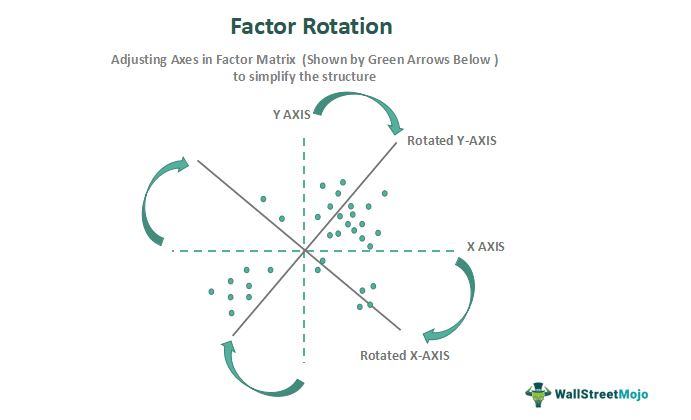
These methods help analysts identify the structure of the factor analysis model for ordinal data in statistics. This approach prevents the misinterpretation of results. In the practical scenario, the process is widely used by institutional investors to undertake influential factors for accurately predicting asset performance in the long run, such as in pension funds.

Factor rotation in factor analysis is a technique that facilitates the shifting of the axes that represent the factors for determining a more simplified and meaningful data structure. However, such a shift in the axes is often executed within the factor space or subspace while not affecting the percentage of variance denoted by the overall subspace. 

The rotation of factors can be either orthogonal or oblique. The selection of the rotation type depends on the correlation between the factors. This correlation is determined from the correlation matrix formed during the factor analysis process. 

The first one is the orthogonal rotation used when there is no correlation between the factors (i.e., the default delta is zero). It includes the following three different methods:

1. Varimax: The varimax factor rotation is one of the most commonly used rotation methods in factor analysis. In this method, the number of those variables is reduced, which has excessive loading on the factors for a more straightforward interpretation of the model.

2. Quartimax: Another technique is the quatimax orthogonal rotation, where the number of factors required for articulating the variables is minimized for better interpretation.

3. Equamax: It is a combination of varimax and quartimax methods, emphasizing simultaneously reducing the number of loading variables and the factors essential for describing the variables. 

However, one must be careful with this method as it may mislead the interpretation due to non-correlated factors. Also, it fails to establish a fair correlation between the factors. 

Next is the oblique rotation, which is useful when there exists a correlation between the factors, whether positive or negative. The two primary oblique rotation methods are: 

1. Direct Oblimin: It is a non-orthogonal or oblique rotation process, where the focus is on overruling the 0 valued default delta by substituting a number equal to or below 0.8.

2. Promax: It is considered to be a more effective oblique rotation technique since it ensures that the factors in the model are correlated. Moreover, its straightforward and spontaneous evaluation makes it suitable for large datasets. 

However, these methods can only be implemented effectively by an experienced researcher. Also, it may not facilitate comparison among different structures while making the factors highly complex and redundant.  

Now, let us move on to some examples where we will gauge the use of factor rotation in factor analysis for different scenarios: 

Example #1

Suppose the matrix below represents two factors, education and employment, loaded with various socio-economic variables:

Now, assuming that the analysis is for the entertainment industry, with no correlation between these factors, orthogonal factor rotation is necessary. Thus, applying the Varimax factor rotation method results in the following factor matrix: 

In the above factor matrix, the factors are adjusted to reach the nearest to the cluster of plotted items, simplifying the structure for analysis. 

Example #2

The factor rotation strategy has found a place in factor investing for interpreting the performance of an investment portfolio in the long run. The Invesco Dynamic US Factor Rotation is one such US core equity model that aims to outperform the market by adjusting and allocating the factors about the US stock market based on various market indicators and macroeconomic signals. 

The primary purpose of this strategy is to bring the axes nearest to the variables for a more simplified and interpretable structure. It is essential for the following reasons:

• Preserves Independence of Factors: The orthogonal rotation methods help researchers to ensure the selected factors are not correlated and independent of each other.
• Simplifies the Structure: The primary aim of employing this strategy is to adjust the factor matrix. This adjustment ensures that the axes move closest to the clustered items, thus simplifying the overall structure.
• Enables Comparison: Using the orthogonal rotation when the researchers get explicit factor matrices, they can easily compare two or more structures to make well-informed decisions.
• Avoids False or Misleading Interpretation: When the axes representing the factors in the analysis are far from the cluster, it makes the structure complex. Moreover, the analysts may misinterpret the results. 
• Provides Realistic Results: The oblique rotation methods can establish a clear correlation between the factors to provide more accurate outcomes.
• Facilitates Factor Investing: Pension fund managers and institutional investors often employ these techniques to outperform the market.
• Enhances Long-Term Portfolio Performance: Such adjustments in the factor matrix used for predictive modeling in the stock market contribute to improving the performance of the overall portfolio. This enhancement is particularly beneficial in the long run.