Risk Parity

What is Risk Parity?

The risk parity approach is a method of portfolio creation in which the amount invested in various assets in the portfolio is determined based on the quantum of risk that security brings to the portfolio and the ultimate goal is to ensure that each asset contributes equally to the overall risk of the portfolio.

By using leverage, the risk parity strategy modifies the Modern Portfolio Theory (MPT). These applications help hedge risks within a portfolio in a way that market parameters and conditions are taken into consideration to make better returns instead of the equation being lopsided in favor of either risk or returns.

• Risk parity is an investment strategy that aims to achieve a balanced risk exposure across different asset classes. It achieves this balance by allocating more weight to low-risk assets.
• Diversifying risk across asset classes is a key objective of risk parity. This diversification helps to reduce the impact of any single asset class on the overall portfolio performance.
• Risk parity portfolios typically allocate more weight to fixed-income assets like bonds. This is because fixed-income assets are generally considered less risky than equities.
• Leverage is common in risk parity strategies as it can enhance returns. 

Risk Parity Explained

Risk parity approach is a portfolio management technique in which the capital is allocated among various assets so that the risk contribution of each asset is equal, and therefore, this approach is so named.

It is advocated that risk parity funds lead to a higher Sharpe ratio, which implies a higher risk-adjusted return; however, leveraging in achieving such an allocation might lead to excessive cash component. And the absolute return is lower. So the investor needs to have clarity that if he is forgoing return, he is doing so to have a less risky portfolio and is okay with this approach.

We look at the risk-adjusted returns while creating a portfolio, keeping in mind the constraints, the return requirement, and the risk tolerance of the investor. However, in the risk parity approach, we allocate only that much amount of money in an asset, which makes the risk of the investment equal to that of the other investments in the portfolio and meets the risk tolerance as specified in the Investor Policy Statement (IPS)

Sometimes this approach is also known as the ‘Risk premia parity’ method, and the proponents believe it of this approach that the Sharpe ratio of such a portfolio is higher as compared to a portfolio that doesn’t follow this approach.

Traditionally, the investment portfolio consists of approximately 60% stock and 40% in fixed income investments. Therefore the maximum risk, almost close to 90%, comes from the investment in stock, and so does the return. In a Risk parity approach, if the asset has a high-risk, high return profile, then the investment in the same is slightly lower, and more increased investment goes to purchases with low-risk short return profiles.

The overall aim is to maximize the Sharpe ratio, so even if the numerator is smaller, the denominator is even smaller because that is the risk of the portfolio, so the overall Sharpe ratio is higher. Following smart art shows the direction in which the portfolio bends in the risk parity approach to strike a balance between riskier and less risky assets.

Examples

Let us understand the risk parity strategy better with the help of a couple of examples. These examples will help us understand the concept in-depth.

Example #1

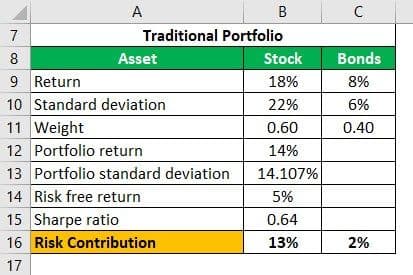
We can take a simple two asset portfolio and do a few calculations to show how the risk parity approach can give a better Sharpe ratio than the traditional portfolio:

Solution:

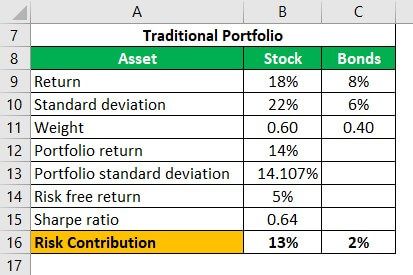
For Traditional Portfolio

Portfolio Return

• Portfolio Return Formula = weighted average of returns = 0.60 x 18% + 0.40 x 8% = 14%

Portfolio Standard Deviation

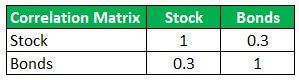
• The rho symbol is the coefficient of correlation between the two assets.

Portfolio Standard deviation =

= 14.107%

Risk Contribution = Weight of Asset * Standard Deviation of Asset

• Stock Risk contribution = 0.60 x 22 = 13.2%
• Bond Risk contribution = 0.40x 6= 2.4%

For Risk Parity Portfolio

Portfolio Return

• Portfolio Return = 0.2143 x 18% +0.7857 x 8% =10 %

Portfolio Standard Deviation

= 67%

Risk Contribution = Weight of Asset * Standard Deviation of Asset

• Stock Risk Contribution = 0.2143 x 22 = 4.71%
• Bond Risk Contribution = 0.7857 x 6 = 4.71%

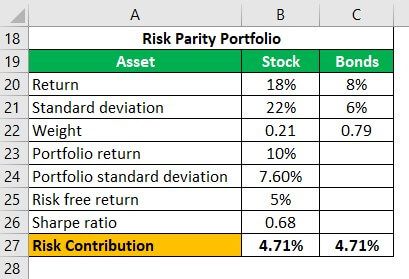
So we can see that the risk parity approach has a higher Sharpe ratio, even with a lower portfolio return.

Example #2

The Teachers Retirement System (TRS) of Texas worth $11.2 billion that provides pension and retirement plans for teachers in public schools and other related organizations has come under serious pressure after struggling to provide enough returns during the turbulent times in the market in 2022-23.

However, since the economy globally seemed to be getting better towards mid-2023, the risk managers who work both internally and externally have said that the fund worth over $170 billion shall improve their risk balancing strategies to provide stable returns irrespective of market conditions.

Moreover, since September 2022, the portfolio has been adjusted to make returns despite the rising rates of inflation in the economy.

Benefits

Let us understand the benefits or advantages of risk parity funds through the explanation below.

• Diversification: In the Risk Parity approach, a smaller portion of the investment is made in all kinds of assets such as stock, bonds, commodities, treasury inflation-protected securities, risk-free assets, and so on. This increases the chances of a good return even in times of lower stock market performance. Therefore, the very first such portfolio was known as the ‘All-weather’ fund and was started in 1996.
• Low cost: Such portfolios are less actively managed and therefore earn a passive return. The fee structure is lower; therefore, those who can’t afford heavy investment management fees prefer such portfolios. The clientele mostly consists of safe return seekers and, therefore, lower risk tolerance, such as pensioners.
• Safer in Recession: When the economy faces the recessionary headwinds, such portfolios can bear it better than a traditional portfolio, which is heavily invested in stocks and other riskier assets. Such funds have lower chances of losing value because the diversified pool can give a cushion to the return and prevent it from falling too much. During the financial crisis of 2007 and for a few years post that, this portfolio gave better performance compared to stock-heavy portfolios.

Limitation

Despite the advantages mentioned above, there are a few factors from the other end of the spectrum that prove to be a hassle. Let us understand the disadvantages of inculcating a risk parity strategy through the points below.

• Market timing risk: Risk Parity portfolios face the risk of market timing because the risk or volatility of the invested asset may not always remain constant. Therefore, it might be the case that the risk goes beyond the prescribed limits, and the portfolio manager is not able to pull out investment promptly.
• Monitoring: Even if active management is not required as much as it is in the case of a more traditional portfolio, rebalancing and monitoring are still needed. Therefore the costs of such portfolios are even higher than completely passive portfolios, which require almost negligible portfolio management.
• Leverage: Greater amount of leverage is required to generate a similar return compared to the traditional portfolio management. However, it is a trade-off to create lower risk, and therefore it is up to the investor to choose.
• Higher allocation to cash: The greater need for leverage requires more cash in hand to meet periodic payments to the leverage providers and meeting margin calls. This is a limitation because cash or nearly cash securities earn very little or no return.

Frequently Asked Questions (FAQs)

Recommended Articles

This has been a guide to what is Risk Parity. Here we explain its examples, portfolio distribution, benefits, and limitations in detail. You may learn more about financing from the following articles -

• Risk Exposure
• Risk Appetite
• Risk Control
• Risk Categories