Tree Diagram

What Is Tree Diagram?

Tree Diagram model is a technique that helps to calculate probability and show it visually. It represents data in the form of a tree branching out into more and more items. Originally used to represent a set of diverging elements arising from a single source, they solve complex problems, especially in mathematics.

One major advantage of the model is that it enumerates all potential outcomes of profit or loss associated with projects. This helps organizations use the information available to make many informed decisions such as finalizing investments, cost and management decisions, business valuations, and probability calculations.

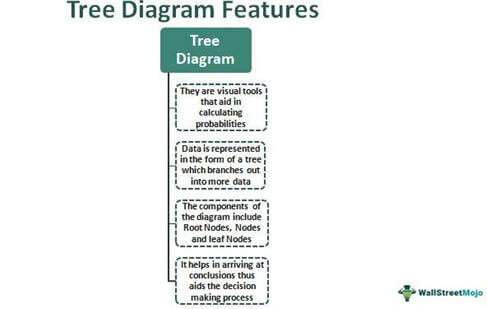
• Tree diagrams are tools that aid in arriving at probable outcomes in probability. They are simple structures that resemble trees.
• It is referred to as a tree due to its connecting lines' resemblance to branches. The components of the diagram include roots, nodes, and leaf nodes. They end when the desired outcome is achieved. Probabilities, when totaled, will be equal to 1.
• They are applicable in many areas apart from probability in statistics and mathematics. For example, decision tree diagrams help an organization or management decide the most practical outcomes, and syntax tree diagrams help understand things like sentence structures.

Tree Diagram In Probability Theory Explained

A tree diagram involves nodes and branches. Any vertex or node can give rise to one or more branches. The lines connecting the vertices are linking lines, and any two vertices a line connects are the vertex pair. The capacity to evolve based on a problem makes these diagrams suitable for portraying a single type of information or a combination of two or more.

Tree diagrams in probability help to express a probability space. They may represent a string of independent events, such as tossing a coin, or conditional probabilities like going out when there is a likelihood of rain. The conditional probability is the likelihood of a certain event or result occurring given a prior event or outcome, such as drawing a deck of cards without substitution. 

Each diagram contains nodes or vertices where each node represents the likelihood of an event happening. For example, the root node represents a specific event that is supposed to happen so that it will have a probability of 1. Each set of subsequent nodes or other joints is an independent extension of the base or parent event.

It is easier to solve a tree diagram in probability as it involves some visualization. Moreover, this can help ease the process of difficulty by logically looking for the next step by branching out possibilities. 

How To Make A Tree Diagram?

Typically, the diagram begins with a single vertex or node that branches into two or more branches. Then, each subsequent node will branch into two or more until the desired outcome arrives. The finished structure then resembles a tree with a trunk and several branches.

A tree diagram in probability is easier to comprehend and analyze with its tree-like structure. The process can evolve through different steps, giving it the appearance of a hierarchy. A conventional tree structure comprises a root node, a node, and a leaf node. It is the same for numbers in math, syntax tree diagram involving literature, and decision tree diagrams drawn to make important decisions.

A tree diagram maker helps to make one; however, the process is simple, and anyone can do it by themself. The basic understanding of the diagram is enough, as follows.

Root Nodes

Root nodes are the foundations from which the structure evolves. The member has no parent node, as it is the starting point. 

Nodes

Nodes, or vertices, are points that emerge from the root nodes. They are connected from the root through lines of connections called links or branches. These links indicate the evolution from the previous step. It, therefore, shows relationships between the members of the structure.

Leaf Nodes

They are otherwise referred to as end nodes as they do not branch out further. 

Examples

Below are some tree diagram examples to understand it better:

Example #1

A simple probability example is the flipping of a coin. There are two sides to a coin: heads and tails. So when one flips a coin, one of two things will happen- It will land on either side, resulting in a head or a tail. In the event of a coin flip, it is taken at a value of 100. So naturally, when there are two outcomes, the chances of either happening are half the total, i.e., 100/2=50% or 0.5. 

Probability always results in 1 here since 0.5+0.5=1. For example, suppose a person tosses a coin twice, then the 0.5 will have two chances of resulting in a head or tail (the possibilities branch out further here), resulting in the formation of 4 outcomes (head, head), (head, tail), (tail, head), (tail, tail). However, the values must be multiplied by 0.5*0.5 = 0.25 (for all four outcomes). And to check probability, we can add all the four 0.25, which will result in 1.

Example #2

Dave wants to give away coins to neighboring kids at random. The bag contains four gold, silver, and copper coins and thus a total of 12 coins. He will take two coins without replacement, and we need to find the probability of him getting different coins.

Here the coins are 4 Gold, 4 Silver, and 4 Copper. Each group of these comes with a probability of 4/12. These form the nodes that have branched from the root, i.e., when the first coin is taken out. Even further, the outcomes branch out more by removing one more coin. In the first round, the coins had an equal chance of being a coin among the three. Now, we are about to find the probability that the second coin is a different color than the first. Here, three scenarios can occur: 

Scenarios

If gold is taken, the chance of taking the gold itself is (3/11). For silver and copper, it is (4/11) each. (Note that the number of events has been reduced from 12 to 11 because one has already occurred). The point is that if the first coin had been gold, the second picking would be done from the remaining number of gold coins, hence 3. 

(2) Silver coin: If the first coin was silver, the chances of the second coin being 

gold are 4/11, silver is 3/11, and copper is 4/11.

(3) A copper coin is:

If the first coin had been copper, then the chance of the second coin being gold is 4/11, silver is 4/11, and copper is 3/11.

The chances of them being different colors can be achieved only when the outcomes end in (gold, silver), (Gold, copper), (silver, gold), (silver, copper), (copper, gold), (copper, silver). Therefore, for all coins, the chance of appearance will be 1/3.

 Therefore, 1/3*4/11=4/33. 

The outcomes will have 4/33 chances of being picked as the second coin. Therefore it has to be added as (4+4+4+4+4+4), which will give a probability of 24/33 overall.

Frequently Asked Questions (FAQs)

Recommended Articles

This article has been a guide to What is Tree Diagram. Here we explain the syntax of the decision tree diagram in probability theory, how to make it, & examples. You can learn more about it from the following articles –

• Euler Diagram
• Venn Diagram
• Fishbone Diagram