Venn Diagram

Venn diagrams refer to the diagrammatic representation of sets using circles. The method was introduced by the English logician John Venn in 1880. It is also known as set diagrams or logic diagrams, and it is used in disciplines like mathematics, statistics, and business studies.

The concept portrays an influence of set theory. A set is a collection of different things or objects or items; for example, it can contain numbers, symbols, or shapes. The set theory focuses on the properties of the collection of objects. It deals with set theory formulas, relations, operations, etc.

• Venn diagrams based on the set theory refer to the diagrammatic representation of sets using circles. English logician John Venn introduced it in 1880.
• It has a wide scope of applications in the academic and business world. For example, it is widely used in mathematics, statistics, computer science, and business management disciplines.
• Common symbols used are U (union), ⋂ (intersection), and A^c  (complement of A).
• The basic formula for a diagram containing two sets is:

n(A U B) = n(A) + n(B) – n (A ⋂ B)

A Venn diagram represents different sets considered for study or comparison using circles. A circular region represents a set. If there is no overlap between circular areas, represented sets have nothing in common, and if the circular region overlaps, there is something in common between the overlapping sets. Furthermore, if a set is a subset of another set, the smaller circle will be seen contained inside the other circle.

The method can contain any number of circles. However, the complexity of diagrammatic representation increases with the number of circles. So, the most common is the usage of two or three circles. Every region in the representation has its significance, conveying specific information. Generally, the overlapped or the intersecting area is highlighted graphically to signify commonality. It is easy to make a Venn diagram; using online Venn diagram templates, MS Office tools, or an online "Venn diagram maker."

It is very similar to the Euler diagram, and it isn't easy to identify the difference between them. The prime difference is that Euler diagrams present only existing relationships; there will be no empty intersections. In contrast, the Venn diagram shows all possible logical relationships and presents intersections even if it is empty.

The basic formula for Venn diagram is:

n(A U B) = n(A) + n(B) – n (A ⋂ B)

Here,

• n(A U B): All elements of sets A and B
• n(A): Number of elements present in set A
• n(B): Number of elements present in set B
• n (A ⋂ B): Number of elements common in both A and B

Let's consider the following Venn diagram example to understand the concept better.

There are 200 employees in a company's sales and marketing division, 140 employees participate in the sales activities, and 120 employees participate in the marketing activities. How many employees take part in both sales and marketing activities? Also, find employees engaged only in sales activities.

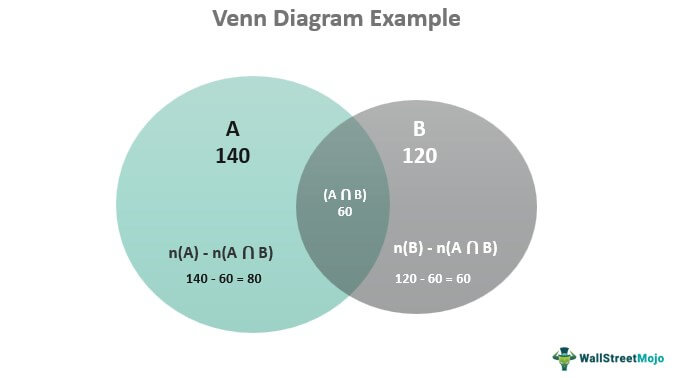
Set A: Employees participating in the sales activities

Set B: Employees participating in the marketing activities

n(A U B)= 200

n(A) = 140

n(B) = 120

n(A ⋂ B) is the number of employees participating in both sales and marketing activities. Hence, applying the formula gives the following:

n(A ⋂ B) = n(A) + n(B) - n(A U B)

n(A ⋂ B) = 140 + 120 – 200

= 60

Employees engaged only in sales = Employees engaged in sales – Employees engaged in both sales and marketing

= n(A) - n(A ⋂ B)

= 140 – 60

= 80

Hence, employees taking part in both sales and marketing activities are 60, and employees engaged only in sales activities are 80.

The most commonly used symbols are the following:

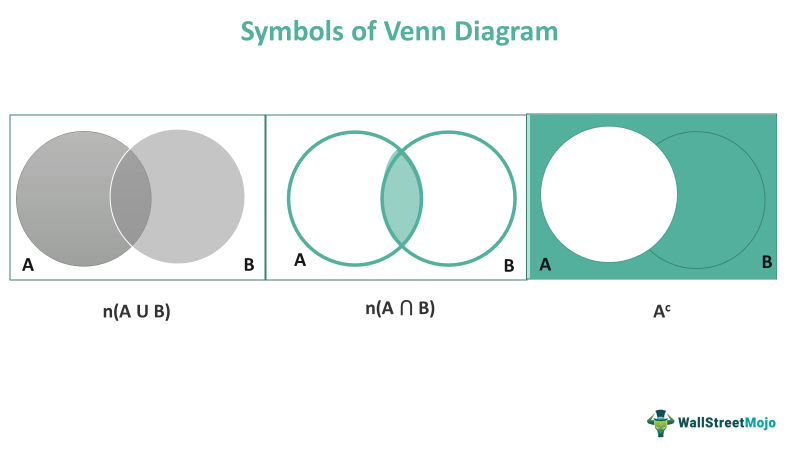
Union (U):

It represents the union of all the sets present in the Venn diagram. So, for example, if there are two sets, A and B, it will be (A U B).                            

Intersection (∩):

It represents the shared elements of all sets present. So, for example, if there are two sets A and B, it will be (A ⋂ B).                                             

Complement: (A^c)

It represents what is not in the specified set. A^c excludes the element in set A. The equation A^c = U/A depicts the A complement, where "U" is the universal set and A is a subset of U, and the complement of set A is all elements of U which are not in A.

• It is used in mathematics and other subjects to easily illustrate complex problems or scenarios. For example, when used properly, Venn diagrams eliminate the need for subject experts to derive an answer using complex steps and formulas, specifically for answers in figures and values. It also makes it easy to represent factors and scenarios that are difficult to explain verbally or mathematically.

• It is used in business presentations to portray various business concepts, visualize ideas and compare competitors. For example, it helps to signify the similarities and differences between different products and prototypes.

This is a Guide to What is Venn Diagram. We explain its example, symbols, formula, applications, and how to make it using options like templates. You can learn more from the following articles - 

• Descriptive Statistics
• Statistics
• Dispersion