Forward Rate Formula

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Formula to Calculate Forward Rate

The forward rate formula helps in deciphering the yield curve which is a graphical representation of yields on different bonds having different maturity periods. It can be calculated based on spot rate on the further future date and a closer future date and the number of years until the further future date and closer future date.

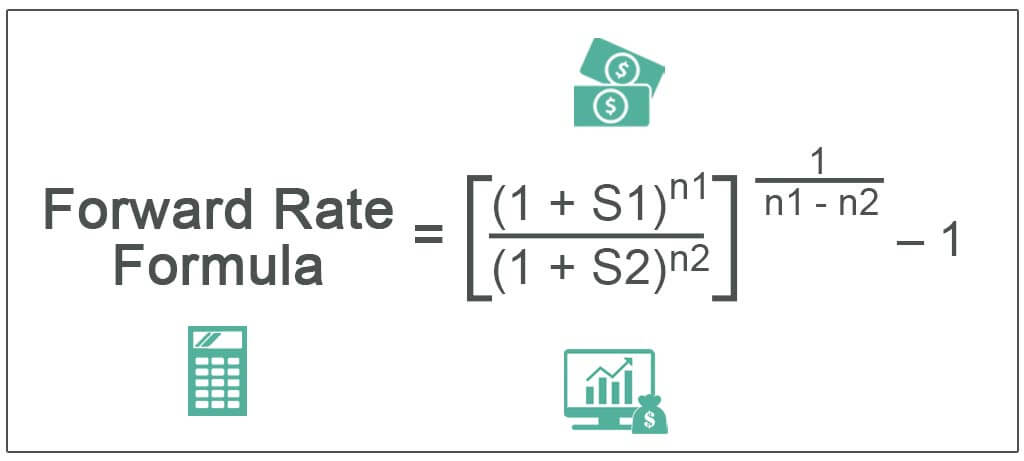
Forward Rate = ^1/(n₁^-n₂⁾ – 1

where S1 = Spot rate until a further future date,

S₂ = Spot rate until a closer future date, n1 = No. of years until a further future date,
n₂ = No. of years until a closer future date

The notation for the formula is typically represented as F(2,1), which means a one-year rate two years from now.

Formula to Calculate Forward Rate

The forward rate formula calculates the expected future interest rate based on prevailing spot rates and the period involved.
This formula estimates the interest rate expected to prevail in the future, enabling market participants to make informed decisions and manage interest rate risk.
The forward rate formula is derived from the concept of the term structure of interest rates, which reflects the relationship between different maturities and their associated interest rates.
The formula assumes that future spot rates align with market expectations and that no arbitrage opportunities exist.

Forward Rate Calculation (Step by Step)

It can be derived by using the following steps:

Firstly, determine the spot rate until the further future date for buying or selling the security, and it is denoted by S1. Also, compute the no. of the year till the further future date, and it is denoted by n1.
Next, determine the spot rate until the closer future date for selling or buying the same security, and it is denoted by S2. Then, compute the no. of the year till the closer future date, and it is denoted by n2.
Finally, the calculation of forward rate for (n1 – n2) no. of years after n2 no. of years is shown below. Forward rate = 1/(n1-n2) – 1

Examples

Example #1

Let us take the example of a company PQR Ltd, which has issued bonds recently to raise money for its upcoming project to be completed in the next two years. The bonds issued with one-year maturity have offered a 6.5% return on investment, while the bonds with two years maturity have offered a 7.5% return on investment. Based on the given data, calculate the one-year rate one year from now.

Given,

The spot rate for two years, S₁ = 7.5%
The spot rate for one year, S₂ = 6.5%
No. years for 2^nd bonds, n₁ = 2 years
No. years for 1^st bonds, n₂ = 1 year

As per the above-given data, we will calculate a one-year rate from now of company POR ltd.

Therefore, the calculation of the one-year forward rate one year from now will be,

F(1,1) = ^1/(n₁^-n₂⁾ – 1

= ^1/(2-1) – 1

One year FOR one year from now= 8.51%

Example #2

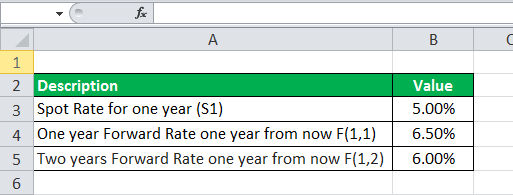
Let us take the example of a brokerage firm that has been in the business for more than a decade. The firm has provided the following information. The table gives a snapshot of the detailed calculation of the forward rate.

Spot rate for one year, S₁ = 5.00%
F(1,1) = 6.50%
F(1,2) = 6.00%

Based on the given data, calculate the spot rate for two years and three years. Then calculate the one-year forward rate two years from now.

Given, S₁ = 5.00%
F(1,1) = 6.50%
F(1,2) = 6.00%

Therefore, the spot rate for two years can be calculated as,

S₂ = ^1/2 - 1

= ^1/2 - 1

Spot Rate for Two Years = 5.75%

Therefore, calculation of spot rate for three years will be,

S₃ = ^1/3 - 1

= ^1/3 - 1

Spot Rate for Three Years= 5.67%

Therefore, the calculation of one-year forward rate two years from now will be,

F(2,1) = ^1/(3-2) – 1

= – 1

Relevance and Uses

The forward rate refers to the rate that is used to discount a payment from a distant future date to a closer future date. It can also be seen as the bridging relationship between two future spot rates, i.e., further spot rate and closer spot rate. It is an assessment of what the market believes will be the interest rates in the future for varying maturities.

For instance, let us assume that Jack has received money today, and he wants to save the money to buy a real estate one year from today. Now, he can invest the money in government securities to keep it safe and liquid for the next year. However, in that case, Jack has two choices: He can either buy a government bond that will mature in one year, or he can opt to buy another government bond that will mature in six months, and then roll over the money for another six-month government bond when the first one matures.

In case both the options generate the same return on investment, then Jack will be indifferent and go with either of the two options. But what if the interest offered is higher for a six-month bond than the one-year bond. In that case, he will make more money by buying the six-month bond now and rolling it over for another six months. Now, It comes into play to calculate the return of the six-month bond six months from now. In this way, it can help Jack to take advantage of such a time-based variation in yield.

Frequently Asked Questions (FAQs)

1. What are the benefits of using the forward rate formula?

The forward rate formula provides benefits such as estimating future interest rates, assisting in the valuation of forward contracts, and facilitating pricing in various financial markets. It enables investors to make informed decisions about borrowing, lending, and investing based on expected future interest rates.

2. What limitations or factors should be considered when using the forward rate formula?

Limitations and factors to consider when using the forward rate formula include assumptions of constant interest rate expectations, the absence of market frictions, and the need for accurate forecasting. Market conditions, economic factors, and external events can affect interest rate movements, making accurate predictions challenging.

3. What is the forward rate formula vs. the cap rate formula?

The forward rate formula calculates expected future interest rates based on the current term structure of interest rates. In contrast, the cap rate formula estimates the capitalization rate used in real estate valuation. The forward rate formula focuses on interest rates, while the cap rate formula is specific to real estate and considers rental income and property values.