Annuity Formula

Formula to Calculate Annuity Payment

The term “annuity” refers to the series of periodic payments to be received either at the beginning of each period or at the end of the period in the future. The formula for annuity payment and annuity due is calculated based on PV of an annuity due, effective interest rate and a number of periods.

The formula based on an ordinary annuity is calculated based on PV of an ordinary annuity, effective interest rate, and several periods.

where,

• PVA _Ordinary = Present value of an ordinary annuity
• r = Effective interest rate
• n = Number of periods

 

Mathematically, the equation for annuity due is represented as,

where,

• PVA _Due = Present value of an annuity due
• r = Effective interest rate
• n = number of periods

How to Calculate Annuity Payment? (Step by Step)

The calculation of annuity payment can be derived by using the PV of ordinary annuity in the following steps:

• Step 1: Firstly, determine the PV of the annuity and confirm that the payment will be made at the end of each period. It is denoted by PVA _Ordinary.
• Step 2: Next, determine the interest rate based on the current market return. Then, the effective rate of interest is computed by dividing the annualized interest rate by the number of periodic payments in a year, and it is denoted by r. r = Annualized interest rate / Number regular payments in a year
• Step 3: Next, determine the number of periods by multiplying the number of periodic payments in a year and the number of years, and it is denoted by n. n = number of regular payments in a year * Number of years
• Step 4: Finally, the annuity payment based on PV of an ordinary annuity is calculated based on PV of an ordinary annuity (step 1), effective interest rate (step 2), and some periods (step 3), as shown above.

The calculation of annuity payment can also be derived by using the PV of an annuity due in the following steps:

• Step 1: Firstly, determine the PV of the annuity and confirm that the payment will be made at the beginning of each period. It is denoted by PVA _Due.
• Step 2: Next, determine the interest rate based on the current market return. Then, the effective rate of interest is computed by dividing the annualized interest rate by the number of periodic payments in a year, and it is denoted by r. r = Annualized interest rate / Number regular payments in a year
• Step 3: Next, determine the number of periods by multiplying the number of periodic payments in a year and the number of years, and it is denoted by n. n = number of regular payments in a year * Number of years
• Step 4: Finally, the annuity payment based on PV of an annuity due is calculated based on PV of an annuity due (step 1), effective interest rate (step 2), and several periods (step 3), as shown above.

Examples

Example #1

Let us take the example of David, who won a lottery worth $10,000,000. He has opted for an annuity payment at the end of each year for the next 20 years as a payout option. Determine the amount that David will be paid as annuity payment if the constant rate of interest in the market is 5%.

Given below is the data used for the calculation of annuity payments.

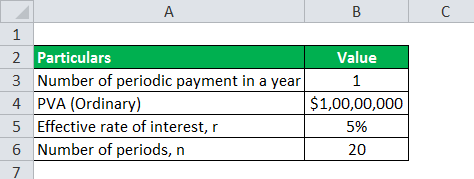
PVA _Ordinary = $10,000,000 (since the annuity to be paid at the end of each year)

Therefore, the calculation of annuity payment can be done as follows –

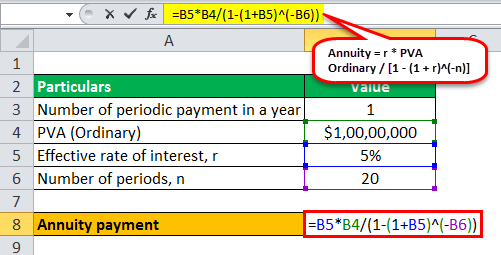
• Annuity = 5% * $10,000,000 / [1 – (1 + 5%)^-20]

Calculation of Annuity Payment will be –

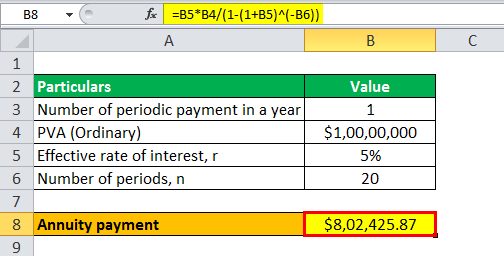
• Annuity = $802,425.87 ~ $802,426

Therefore, David will pay annuity payments of $802,426 for the next 20 years in case of ordinary annuity.

Example #2

Let us take the above example of David and determine the annuity payment if paid at the beginning of each year with all other conditions the same.

We will use the same data as the above example for the calculation of Annuity payments.

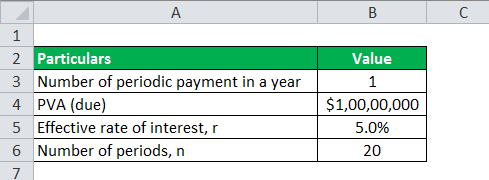
Therefore, the calculation of annuity payment can be done as follows –

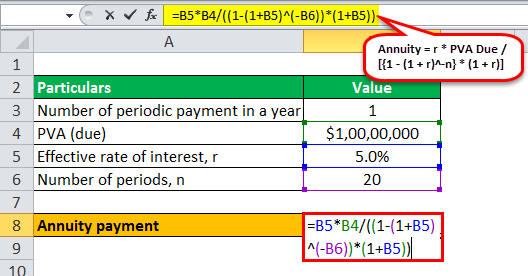
• Annuity = r * PVA _Due / [{1 – (1 + r)^-n} * (1 + r)]
• Annuity = 5% * $10,000,000 / [{1 – (1 + 5%)^-20} * (1 + 5%)]

Calculation of Annuity Payment will be –

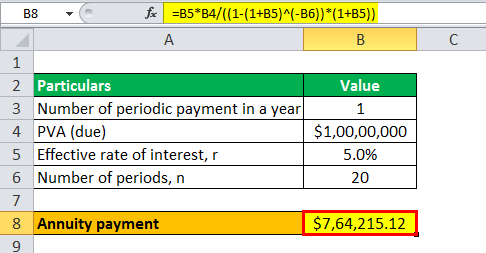
• Annuity = $764,215.12 ~ $764,215

Therefore, David will pay annuity payments of $764,215 for the next 20 years in case of an annuity due.

Annuity Calculator

You can use the following Annuity Calculator.

Relevance and Uses

The annuity payment is one of the applications of the time value of money, which is further indicated by the difference between annuity payments based on ordinary annuity and annuity due. The lower annuity payment for an annuity is that the money is received at the start of each period. It is believed that the funds will be invested in the market, and interest will be earned during that period.

The equation for annuity payment finds application in calculating income annuities, amortized loans, lottery pay-outs, structured settlements, and any other type of fixed periodic payments.

Annuity Formula Video

Recommended Articles

This article has been a guide to Annuity Formula. Here we learn how to calculate Annuity Payments for Ordinary and due annuity along with practical examples and a downloadable excel template. You can know more about financial analysis from the following articles –

• Annuity vs. Perpetuity
• Effective Annual Rate Formula
• Formula of Present Value of an Annuity 
• Tax-Deferred Annuity