Deferred Annuity Formula

Deferred annuity formula is used to calculate the present value of the deferred annuity which is promised to be received after some time and it is calculated by determining the present value of the payment in the future by considering the rate of interest and period of time.

An annuity is the series of periodic payments received by an investor on a future date, and the term “deferred annuity” refers to the delayed annuity in the form of installment or lump-sum payments rather than an immediate stream of income. It is basically the present value of the future annuity payment. The formula for a deferred annuity based on an ordinary annuity (where the annuity payment is made at the end of each period) is calculated using ordinary annuity payment, the effective rate of interest, number of periods of payment, and deferred periods.

Deferred Annuity based on an ordinary annuity, is represented as,

where,

• P _Ordinary = Ordinary annuity payment
• r = Effective rate of interest
• n = No. of periods
• t = Deferred periods

The formula for a deferred annuity based on annuity due (where the annuity payment is made at the start of each period) is calculated using annuity payment due, effective rate of interest, a number of periods of payment, and deferred periods.

Deferred Annuity based on annuity due, is represented as,

where

• P _Due = Annuity payment due
• r = Effective rate of interest
• n = No. of periods
• t = Deferred periods

• Deferred annuities are insurance contracts designed to provide a steady income stream during retirement. They enable individuals to accumulate funds over a specified period before commencing receipt of payments.
• The accumulation phase of a deferred annuity involves making contributions and allowing the funds to grow tax-deferred until the annuitization or distribution phase begins.
• Deferred annuities offer the potential for long-term growth and can serve as a reliable source of retirement income. 
• Deferred annuities provide a range of options, including fixed or variable interest rates, indexed returns, and various payout methods. 

The formula for deferred annuity using ordinary annuity can be derived by using the following steps:

• Step 1: Firstly, ascertain the annuity payment and confirm whether the payment will be made at the end of each period. It is denoted by P Ordinary.
• Step 2: Next, calculate the effective rate of interest by dividing the annualized rate of interest by the number of periodic payments in a year and it is denoted by r. r = Annualized rate of interest / No. periodic payments in a year
• Step 3: Next, calculate the total number of periods, which is the product of a number of years and number of periodic payments in a year, and it is denoted by n. n = No. of years * No. of periodic payments in a year
• Step 4: Next, determine the period of payment deferment, and it is denoted by t.
• Step 5: Finally, the deferred annuity can be derived using ordinary annuity payment (step 1), an effective rate of interest rate (step 2), a number of periods of payment (step 3), and deferred periods (step 4), as shown below.

Deferred Annuity = P _Ordinary * /

The formula for deferred annuity using annuity due can be derived by using the following steps:

• Step 1: Firstly, ascertain the annuity payment and confirm whether the payment will be made at the start of each period. It is denoted by P Due.
• Step 2: Next, calculate the effective rate of interest by dividing the annualized rate of interest by the number of periodic payments in a year, and it is denoted by r. i.e., r = Annualized rate of interest / No. periodic payments in a year
• Step 3: Next, calculate the total number of periods, which is the product of the number of years and number of periodic payments in a year, and it is denoted by n. i.e., n = No. of years * No. of periodic payments in a year
• Step 4: Next, determine the period of payment deferment, and it is denoted by t.
• Step 5: Finally, the deferred annuity can be derived using annuity payment due (step 1), the effective rate of interest rate (step 2), the number of periods of payment (step 3), and deferred periods (step 4) as shown below.

Deferred Annuity = P Due * /

Let us take the example of John, who got a deal to lend $60,000 today, and in return, he will receive twenty-five annual payments of $6,000 each. The annuity will start five years from now, and the effective rate of interest will be 6%. Determine whether the deal is a feasible one for John if the payment is an ordinary annuity and annuity due.

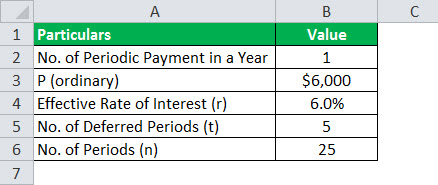
• Given, P _Ordinary = $6,000,000
• r = 6%
• n = 25 years
• t = 5 years

Calculation of Deferred Annuity if payment is Ordinary Due

Therefore, the deferred annuity can be calculated as,

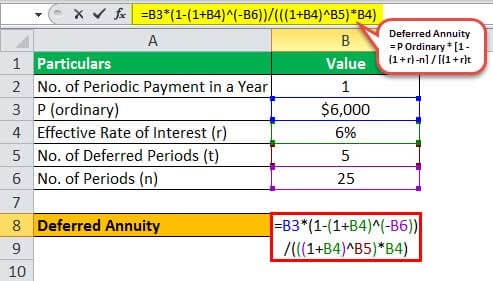
• Deferred Annuity = $6,000 * /

Deferred Annuity will be -

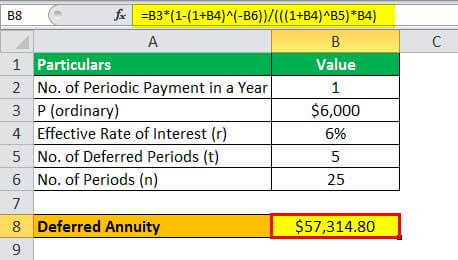
Deferred Annuity = $57,314.80 ~ $57,315

n this case, John shouldn’t lend the money as the value of the deferred annuity is less than $60,000.

Calculation of Deferred Annuity if payment is Annuity Due

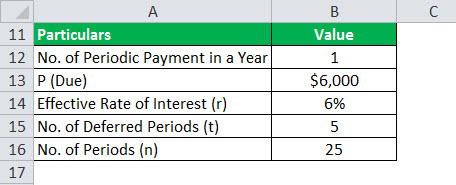
• Given, P _Due = $6,000,000
• r = 6%
• n = 25 years
• t = 5 years

Therefore, the deferred annuity can be calculated as,

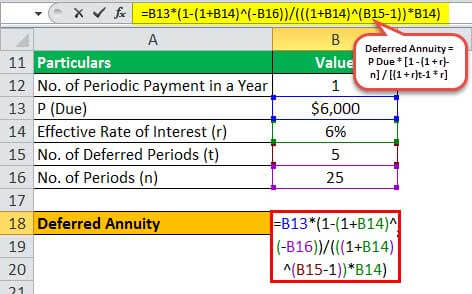
• Deferred Annuity = $6,000 * /

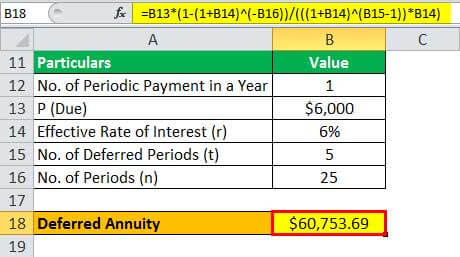
Deferred Annuity = $60,753.69 ~ $60,754

In this case, John should lend the money as the value of the deferred annuity is more than $60,000.

From the perspective of an investor, deferred annuities are mainly useful for the purpose of tax deferral of earnings because of a lack of restrictions on the amount of its annual investment coupled with the guarantee of the lifelong source of income. However, one of the major drawbacks of an annuity is that its gains are taxed at the ordinary income tax rate, which is higher than the long-term capital gains tax rate.

This has been a guide to Deferred Annuity Formula. Here we learn how to calculate the Deferred Annuity for due and ordinary payment along with the practical examples and downloadable excel sheet. You can learn more about financing from the following articles –

• Annualized Rate of Return
• What is Tax-Deferred Annuity?
• Annuity vs Perpetuity
• Simple Random Sampling