Table Of Contents
What Is Present Value Of An Annuity Formula?
The present value of annuity formula is calculated by determining present value which is calculated by annuity payments over the time period divided by one plus discount rate and the present value of the annuity is determined by multiplying equated monthly payments by one minus present value divided by discounting rate.
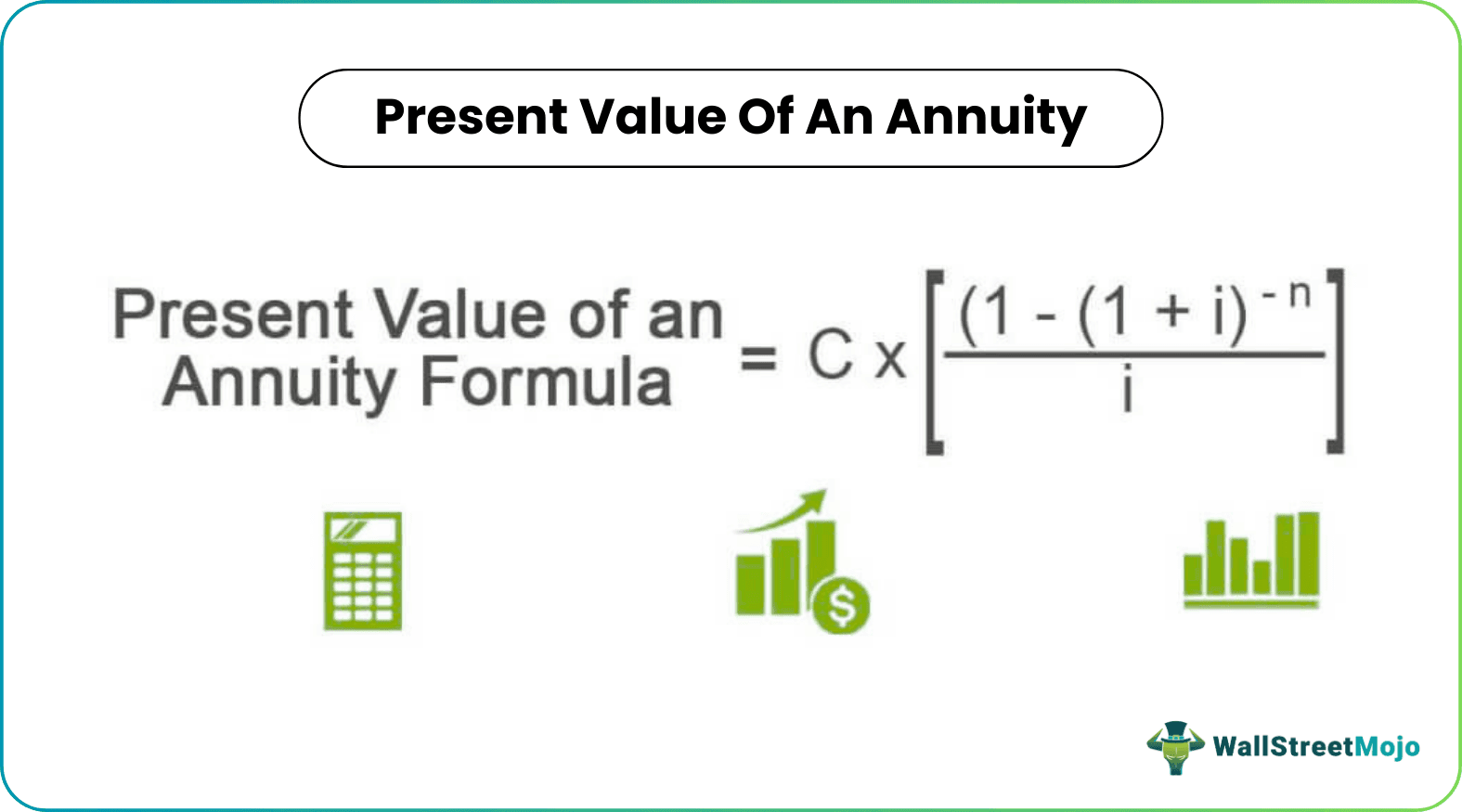
Thus, the formula gives us the current value of all the payments that will happen in the future where the discount rate or the rate of return is predetermined. This present value denotes the amount which an investor will invest now so that they can get a fixed payment in the future.
Key Takeaways
- The present value of a perpetuity is a financial concept used to calculate the current worth of an infinite series of cash flows that are expected to continue indefinitely at a fixed interval and constant amount.
- The formula for calculating the present value of a perpetuity is PV = C / r, where PV represents the current value, C means the cash flow amount, and r represents the discount rate or required rate of return.
- The present value of infinity is used in various financial calculations, such as determining the value of certain types of bonds, preferred stock, or perpetually growing dividends.
- The discount rate used in the present value of perpetuity calculation reflects the opportunity cost of investing in similar assets with comparable risk and return profiles.
Present Value Of An Annuity Formula Explained
The net present value of an annuity formula will determine at a given period, the present value of several future timely interval payments. The PV of annuity formula can be seen from the formula that it depends upon the time value of money concept, in which a one-dollar amount of money in the current day is more worthy than the same dollar that shall be due at a date which is going to happen in future. Also, the PV of the annuity formula takes care of the frequency of payment, whether it’s annual, semi-annual, monthly, etc. and accordingly does calculation or say compounding. Also, one has to be cautious while using the net present value of an annuity formula as one needs to determine if the payments are made at the beginning of the period or at the end of the period, as the same can affect the values of cash flows due to compounding effects
How To Calculate?
Now let us try to understand the calculation. The formula given below is related to the ordinary annuity, which pays the interest at the end of the accounting period, not at the beginning. However, the present value of an annuity formula excel is also useful for the calculation, which is given later in the article.
PV of an Annuity = C x
Where,
- C is the cash flow per period
- i is the rate of interest
- n is the frequency of payments
The cash flows are the series of funds that the investor expects to receive in the future and whose current value we are trying to calculate. The interest rate or the discount rate is very important. It is an assumed rate that actually represents the time value of money. A higher rate will reduce the current value because it means that the future amount is heavily discounted to get the present value. The variable n denotes the number of times the payment will be made.
Examples
Let us try to understand the concept with the help of some suitable examples. It can also be calculated by using present value of an annuity formula excel, as given below.
Example #1
Suppose that there is an annuity payment of $1,000 for the next 25 years beginning at every end of the year. You are required to compute the present value of the annuity, assuming a rate of interest is 5%.
Solution:
Here the annuities begin at the end of the year, and therefore, n will be 25, C is $1,000 for the next 25 years, and i is 5%.
Use the following data for the calculation of the PV of an annuity.
- Cash flow per Period (C): 1000.00
- Number of Period (n): 25.00
- Rate of Interest (i): 5.00%
So, the present value of simple annuity formula can be used as follows –

Present Value of simple Annuity formula will be -

= $1,000 x
Present Value of an Annuity = 14,093.94
Example #2
John is currently working in an MNC where he is paid $10,000 annually. In his compensation, there is a 25% portion, which will be paid an annuity by the company. This money is deposited twice in a year, starting 1st July and second is due on the 1st of January and will continue till the next 30 years, and at the time of redemption, it would be tax-exempt.
He was also given an option at the time of joining to take $60,000 at once, but that would be subject to tax at the rate of 40%. You are required to assess whether John should take the money now or wait until 30 years to receive the same, assuming he is not in the requirement of funds, and the risk-free rate in the market is 6%.
Solution
Here, the annuities begin at the end of the semi-annually and therefore n will be 60 (30*2), C is $1,250 ($10,000 * 25% / 2) for next 30 years and i is 2.5% (5%/2).
Use the following data for the calculation of the present value of an annuity.
- Cash flow per Period (C): 1250.00
- Number of Period (n): 60.00
- Rate of Interest (i): 2.5%
So, the calculation of the (PV) present value of an annuity formula can be done as follows –

Present Value of the Annuity will be -

= $1,250 x
Present Value of an Annuity = $38,635.82
Hence, if John opts for an annuity, then he would receive $38,635.82.
The second option is he opts for $60,000, which is before tax, and if we deduct a tax of 40%, then the amount in hand will be $36,000.
Therefore, John should opt for annuity since there is a benefit of $2,635.82
Example #3
Two different retirement products are being offered to Mrs. Carmella as she is nearing retirement. Both of the products will start their cash flow at the age of 60 years and continue annuity till 80 years of age. Below are more details of the products. You are required to compute the present value of the annuity and advise, which is the better product for Mrs. Carmella?
Assume Rate of interest 7%.
1) Product X
Annuity Amount = $2,500 per period. Payment frequency =Quarterly.Payment will be at the beginning of the period.
2) Product Y
Annuity Amount = 5,150 per period. Payment frequency =Semi-Annually. Payment will be at the end of the period
Given,
| Particulars | Product X | Product Y |
|---|---|---|
| Cash flow per Period (C) | 2500.00 | 5150.00 |
| Number of Periods (n) | 79.00 | 40.00 |
| Rate of Interest (i) | 1.75% | 3.50% |
Solution:
Here, the annuities for product x begins at the beginning of the quarter, and therefore, n will be 79 as the payment is made at the beginning of the annuity (20*4 less 1), C is $2,500 for the next 20 years, and it is 1.75% (7%/4).
So, we calculate present value of annuity formula for a product X as follows –

Present Value of an Annuity for Product X will be -

=$2,500 x
Present Value of Annuity = $106,575.83
Now we need to add $2,500 to above present value since that was received at the start of the period and hence total amount will be 1,09,075.83
The 2nd option is paying semi-annually. Hence n will be 40 (20*2), i will be 3.50% (7%/2), and C is $5,150.
So, the calculation of the PV of an annuity for a product Y can be done as follows –

Present Value of Annuity for Product Y will be -

= $5,150 x
Present Value of Annuity = $ 109,978.62
There is only $902.79 excess when opted for option 2. Hence Mrs. Carmella should select opt 2.
Benefits
Some benefits of the formula as given below:
- It is a very good method for financial planning, where the investor can understand the present worth of the future cash flows and its impact on the overall financial condition.
- It is possible to evaluate any investment opportunity and compare them to check whether they are viable enough to give profitable returns in future.
- The formula is quite important not only in calculating the retirement options, but this can also be used for cash outflows in case of capital budgeting, where there could be an example of rent or periodic interest paid, which are mostly static; hence those can be discounted back by using this annuity formula.
- Businesses or individuals can use this formula to decide whether they will prefer to receive a lump sum payment for the future annuities now or get the cash flows in future. Thus, this calculation helps to decide which option is better from the financial point of view.
- Since it takes into account the time value of money, it clearly reflects the risk factor, which is the opportunity cost of not taking the money now.
Limitations
Even though it is a great tool for financial assessment, there are some limitations to calculate present value of annuity formula.
- The formula assumes that interest rate which may not correctly reflect the true present value of the cash flows. The rates are also assumed to be fixed, whereas they may fluctuate over a time period.
- Since the inflation factor is not accounted for, it does not reflect the real-world scenario because the inflation affects the purchasing power.
- The calculation assumes that the cash flow will be reinvested at the same interest rate, which may not always be true.

