Table Of Contents
Formula to Calculate PV of Ordinary Annuity
Ordinary Annuity Formula refers to the formula that is used to calculate the present value of the series of an equal amount of payments that are made either at the beginning or end of the period over a specified length of time. As per the formula, the present value of an ordinary annuity is calculated by dividing the Periodic Payment by one minus one divided by one plus interest rate (1+r) raise to the power frequency in the period (in case of payments made at the end of period) or raise to the power frequency in the period minus one (in case of payments made at the beginning of period) and then multiplying the resultant with the rate of interest.
The formula is given below
Present Value of Ordinary Annuity (Beg) = r * P / {1 – (1+r)-(n-1)}
Present Value of Ordinary Annuity (End) = r * P / {1 – (1+r)-(n)}
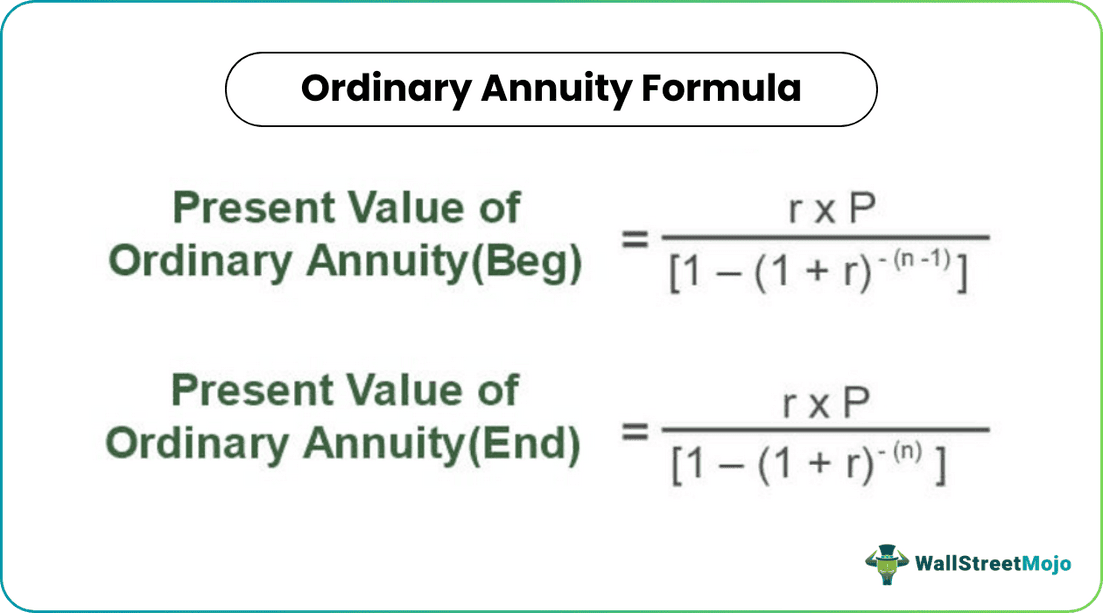
Where,
- P is the Periodic Payment
- r is the interest rate for that period
- n will be a frequency in that period
- Beg is Annuity due at the beginning of the period
- The end is Annuity due at the end of the period
Key Takeaways
- The ordinary annuity formula determines the present value of a series of equal payments made at the beginning or end of each period over a defined length of time.
- The ordinary annuity formula is paramount in finance as it enables precise calculations of the present value of recurring payments, aiding investors and analysts.
- Ordinary annuities can include interest payments from bond issuers. These payments can be quarterly or semi-annual, and they often comprise regular dividends.
Explanation
The present value of ordinary annuity takes into account the three major components in its formula. PMT, which is nothing but r*P, which is the cash payment, then we have r, which is nothing, but the prevailing market interest rate, P is the present value of initial cash flow, and finally, n is the frequency or the total number of periods. Then there are two types of payment: one annuity, which is due at the beginning of the period, and the second one is due at the end of the period.
Both the formulas have a slight difference in that in one, we compound by n, and in another, we compound by n-1; that's because the payment 1st that is made will be made today, and hence no discounting is applied to the 1st payment for the beginning annuity.
Examples
Example #1
Keshav has inherited $500,000 as per the agreement. However, the agreement stated that the payment would be received as an annuity for the next 25 years. You are required to calculate the amount that shall be received by Keshav, assuming the interest rate prevailing in the market is 7%. You can assume that the annuity is paid at the end of the year.
Solution
Use the following data can be used for the calculation
- Present Value of Lumpsum Amount (P): 10000000
- Number of Periods (n): 25
- Rate of Interest (r): 7%
Therefore, the calculation of the ordinary annuity (end) is as follows.

=500,000* 7% /{1-(1+7%)-25}
Ordinary Annuity Value (end) will be -

Example #2
Mr. Vikram Sharma has just settled in his life. He got married to a girl he wished for and got the job he had been looking for for a long time. He has done his graduation from London, and he has also inherited $400,000 from his father, who is his current savings.
He and his wife are looking to buy a house in the town worth $2,000,000. Since they don’t own that much funds, they have decided to take a bank loan whereby they will be required to pay 20% from their pocket, and the rest would be taken care of by the loan.
The Bank charges an interest rate of 9%, and the installments need to be paid monthly. They decide to go for a ten years loan and have confidence that they shall repay the same sooner than the estimated ten years.
You are required to calculate the present value of the installments that they will be paying monthly starting at the month.
Solution
Use the following data for the calculation of ordinary annuity due at a beginning period.
- House Value: 2000000
- Loan Ratio: 80%
- Present Value of Lumpsum Amount (P): 1600000
- Number of Periods (n): 10
- Number of Periods in Months: 120
- Rate of Interest (r): 9%
- Rate of Interest Monthly: 0.75%
Here, Mr. Vikram Sharma and his family have taken a housing loan, which equals $2,000,000 * (1 – 20%) to $1,600,000.
Now we know the present value of the lump sum amount that shall be paid, and now we need to calculate the present value of monthly installments using the below start of the period formula.
The interest rate per annum is 9%. Therefore the monthly rate shall be 9%/12 is 0.75%.
Therefore, the calculation of the ordinary annuity (Beg) is as follows.

= 0.75%*1,600,000/{1-(1+0.75%)-119}
Ordinary Annuity Value (Beg) will be -

Example #3
Motor XP has been recently made available in the market, and to promote its vehicle, the same has been offered at a rate of 5% for the initial three months of launch.
John, who is aging 60 years now, is eligible for an annuity that he purchased 20 years ago. Wherein he made the lump sum amount of 500,000, and the annuity will be paid yearly till 80 years of age, and the current market rate of interest is 8%.
He is interested in buying the model XP motor and wants to know whether the same would be affordable for the next ten years if he takes it on EMI, payable yearly. Assume that the price of the bike is the same as the amount he invested in the annuity plan.
Are you required to advise John where his annuity will meet the EMI expenses?
Assume both are incurred at the end of the year only.
Solution
In this case, we need to calculate two annuities: one is a normal one, and another is a loan annuity.
| Particulars | Annuity | Bike |
|---|---|---|
| Present Value of Lumpsum Amount (P) | 500000 | 500000 |
| Number of Period (n) | 20 | 10 |
| Rate of Interest (r) | 8.00% | 5.00% |
Annuity
Therefore, the calculation of the ordinary annuity (end) is as follows

= 500,000 * 8%/{1-(1+8%)-20}
Ordinary Annuity Value (end) will be -

Motor XP
Therefore, the calculation of the ordinary annuity (end) is as follows

= 5%*500,000/{1-(1+5%)-10}
Ordinary Annuity Value (end) will be -

There is a gap of 13,826.18 between the Annuity payment and Loan payment, and hence either John should be able to take out from pockets, or he should extend the EMI till 20 years, which is the same as an annuity.
Relevance and Uses
In real-life examples, ordinary annuities could be interest payments from bond issuers. Those payments are generally paid monthly, quarterly, or semi-annually and further dividends are paid quarterly by a firm that has maintained a stable payout for years. PV of an ordinary annuity will be majorly dependent upon the current market interest rate. Due to the TVM, in case of rising interest rates, the present value will decrease, while in the scenario of declining interest rates, it shall lead to an increase in the annuities present value.

