Exponential Growth Formula
Last Updated :
-
Blog Author :
Edited by :
Reviewed by :
Table Of Contents
What is Exponential Growth Formula?
The exponential growth formula refers to the increase due to the compounding of the data over time. It, therefore, follows a curve representing an exponential function. In finance, it refers to the compounding effect of investments and savings for a long period where the compounding effect takes effect and the returns from such investments result in significant returns.
However, in the case of continuous compounding, the equation calculates the final value by multiplying the initial value and the exponential function, raised to the power of the annual growth rate into the number of years. This metric is used to calculate the multifold growth across domains such as botany, biology, economics, and mathematics, and even to calculate the population exponential growth formula.
Table of contents
- Exponential growth refers to the increase resulting from data compounding over time, following an exponential function curve.
- The formula to calculate exponential growth is Final value = Initial value * (1 + Annual Growth Rate/No of Compounding )^(No. of years * No. of compounding). For continuous compounding, the formula is Final value = Initial value * e^(Annual growth rate * No. of years).
- The exponential growth formula is essential for financial analysts as it helps calculate compound returns. It demonstrates the power of compounding and its significance for investors with long holding periods.
Exponential Growth Formula Explained
The exponential growth formula represents a particular data set's multifold or "exponential" growth over a specific period. This metric is used by professionals of various domains suitable, from branches of science like botany, and biology, to economists and financial experts.
The simplest and the most common example of this phenomenon is found in savings accounts with interest rates that are credited on a compounding basis. Initially, the growth might seem similar to other forms of investment. However, a sharp return increase can be seen over a while.
This use of this metric to calculate long-term growth can be tricky for an investment in volatile asset classes, such as stock market as it does not follow a fixed rate of return or a yearly return scheme to be able to calculate it with this metric.
Similar metrics that use probability distribution, such as the Monte Carlo Simulation have gained more attraction and usage over the years.
The formula for the calculation is as discussed below:
Mathematically, it represents as below,
How To Calculate?
Let us understand how to calculate using the exponential growth formula through the step-by-step explanation below.
- Firstly, determine the initial value for which the final value one has to calculate. For instance, it can be the present value of money in the time value of money calculation.
- Next, determine the annual growth rate, which one can decide based on the type of application. For instance, if the formula is to calculate a future value formula of a deposit, then the growth rate will be the rate of return expected from the market situation.
- The tenure of the growth in terms of the number of years figured out, i.e., how long the value will be under such a steep growth trajectory.
- Now, determine the number of compounding periods per year. The compounding can be quarterly, half-yearly, annually, continuous, etc.
- Finally, the exponential growth is to calculate the final value by compounding the initial value (Step 1) by using an annual growth rate (Step 2), the number of years (Step 3), and the number compounding per year (Step 4), as shown above.
On the other hand, the formula for continuous compounding is to calculate the final value by multiplying the initial value (Step 1) and the exponential function raised to the power of the annual growth rate (Step 2) over several years (Step 3), as shown above.
Examples
Let us understand the intricate details of this concept with the help of a couple of examples. Through these examples, we shall understand the calculation of compounding on a monthly, quarterly, and yearly compounding. Additionally, we will also learn the impact of the continuous exponential growth formula.
Example #1
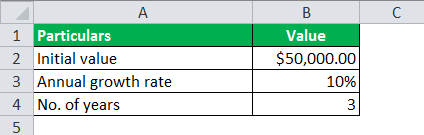
Let us take the example of David. He deposited $50,000 in his bank account for three years at a 10% interest rate. Determine the value of the deposited money after three years if the compounding is:
- Monthly
- Quarterly
- Half Yearly
- Annually
- Continuously
Monthly Compounding
No. of compounding per year = 12 (since monthly)
The calculation of exponential growth, i.e., the value of the deposited money after three years is done using the above formula,
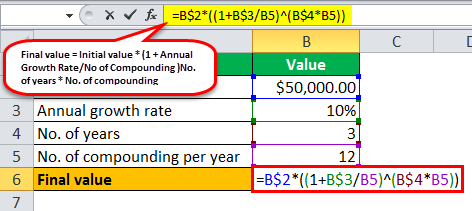
- Final value = $50,000 * (1 +10%/12 )3 * 12
The calculation will be-
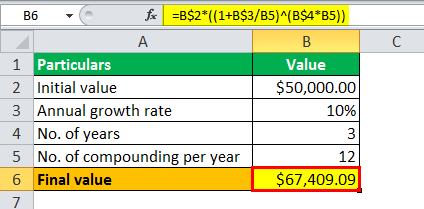
- Final value = $67,409.09
Quarterly Compounding
No. of compounding per year = 4 (since quarterly)
The calculation of exponential growth, i.e., the value of the deposited money after three years, is done using the above formula as,
Final value = $50,000 * (1 + 10%/4 )3 * 4
The calculation will be-
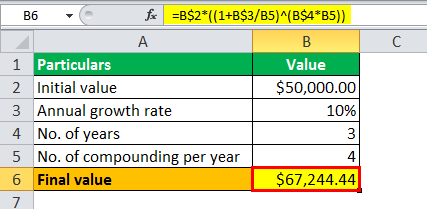
- Final value = $67,244.44
Half Yearly Compounding
No. of compounding per year = 2 (since half-yearly)
The value of the deposited money after three years done using the above formula:
Final value = $50,000 * (1 + 10%/2 )3 * 2
Calculation of Exponential Growth will be-
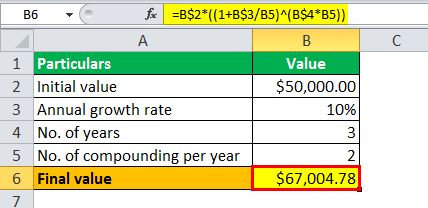
- Final value = $67,004.78
Annual Compounding
No. of compounding per year = 1 (since annual)
The calculation of exponential growth, i.e., the value of the deposited money after three years, is done using the above formula as,
Final value = $50,000 * (1 + 10%/1 )3 * 1
Calculation of Exponential Growth will be-
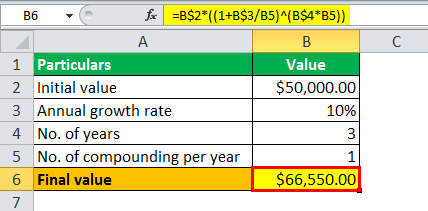
- Final value = $66,550.00
Continuous Compounding
Since continuous compounding, the value of the deposited money after three years money is calculated using the above formula as,
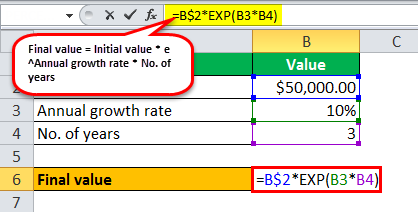
Final value = Initial value * e Annual growth rate * No. of years
Final value = $50,000 * e 10% * 3
Calculation of Exponential Growth will be-
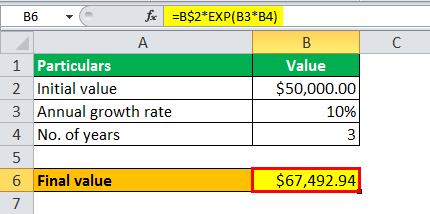
- Final value = $67,492.94
Example #2
In 2023, Bitcoin users issued over 10,000 BRC20 tokens that led to a sharp growth in the ordinal inscriptions of the cryptocurrency giant. The issue of these 10,000 tokens stood at approximately $497.75 million, comprising of 24,677 unique tokens in May 2023.
Bitcoin and Ethereum had similar functionalities like new tokens and non-fungible token (NFT) assets. This shift in strategy saw an exponential rise in the value of long-term holders of bitcoin. The growth in the week of the issue of these tokens alone was recorded at an impressive 16.56%
Calculator
We have provided a calculation for the perusal of the reader. The first-hand experience of using this metric might help with understanding the concept better.
Relevance and Uses
A financial analyst needs to understand the exponential growth equation since it primarily calculates compound returns. The enormity of the concept in finance demonstrates the power of compounding to create a large sum with a significantly low initial capital. For the same reason, it holds great importance for investors who believe in long holding periods.
Frequently Asked Questions (FAQs)
The exponential growth formula is applicable when you want to calculate the future value of an investment or data that follows a compounding pattern over time. It is commonly used in financial analysis, forecasting, and modeling scenarios.
The exponential growth formula assumes that the growth rate remains constant throughout the compounding period and no external factors significantly impact the growth rate. It assumes that the compounding occurs at regular intervals and that the underlying data follows an exponential function.
The exponential growth formula assumes a constant growth rate, which may not hold true in real-world situations where growth rates can vary or fluctuate. It also assumes that the compounding intervals are fixed, whereas, in practice, compounding may occur at irregular intervals. Additionally, the formula does not account for external factors or events that can influence the growth pattern, making it less accurate in unpredictable or uncertain scenarios.
Recommended Articles
This article is a guide to what is Exponential Growth Formula. Here we explain how to calculate Exponential Growth with examples and a downloadable Excel sheet. You can learn more about financing from the following articles: -
