Fractional Diffusion Equation

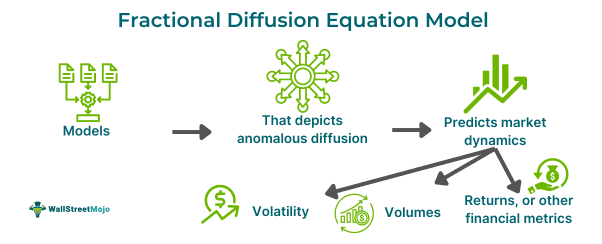
Fractional diffusion equations depict anomalous diffusion occurring on fractals. These are physical objects with fractional dimensions, such as certain amorphous semiconductors or highly porous materials. These equations are significant among recent models for effectively describing diverse and complex diffusion phenomena.

The equation serves as an apt model for diffusion occurring in disordered media characterized by dissipative processes like trapping or recombination. Under these, an initial exponential distribution exists either in the spatial axis or energy. The fractional decay aspect does not explicitly account for the initial excitation. The ultra-short time-scale relaxation processes are responsible for forming the initial exponential distribution.

The fractional diffusion equation is a differential equation that incorporates fractional derivatives to describe the behavior of diffusing quantities. Equations and related models are used in the analysis of financial time series. Financial time series are sequential data points that refer to market or asset prices, volumes, returns, or other financial metrics over time. These data are vital for comprehending market dynamics, making investment choices, and researching financial market behavior.

These equations and similar models capture the intricate dynamics and anomalous patterns commonly seen in financial markets. They help explain phenomena such as long-range dependence, heavy-tailed distributions, and non-Gaussian behavior. By incorporating fractional derivatives, these models offer a more precise depiction of the underlying mechanisms shaping financial time series.

Financial time series often display power law decay. They are explained better by models that go beyond Gaussian distribution and Brownian motion models. Various models, including fractional stochastic processes and diffusion equations, have been proposed to address this. However, they struggle to capture the complexity of financial dynamics, such as seasonal changes and temporary crises, without affecting the corresponding time series' long-term scaling properties. A space-time fractional diffusion equation (space fractional diffusion equation and tempered fractional diffusion equations) of varying order is used to model such financial activities.

The model allows for individual selection of spatial and temporal derivative orders for each time interval, enabling the modeling of temporary restricted anomalies. Additionally, the fixed ratio of spatial and temporal derivatives orders ensures an accurate description of the scaling properties across the entire process. This way, the equations are used fully in many fields.

Let us look into a few examples to understand the concept better:

Example #1

Suppose investor David is analyzing the options market for a stock with heavy-tailed volatility patterns. He uses fractional diffusion models to capture these dynamics and make informed decisions. David calibrates a model using historical options data to estimate parameters 𝛼 and 𝛾, understanding memory effects and risk redistribution mechanisms.

The model reveals that the options market is pricing short-term options higher than long-term options, suggesting a memory effect. This insight informs David to adjust his portfolio construction and delta-hedging policies, incorporating the fractional diffusion model's insights into the sensitivity of his portfolio to changes in the underlying asset's price. This informed decision-making enhances his ability to navigate the options market and achieve better risk-adjusted returns.

However, investors should conduct thorough research and analysis. They may consider various factors beyond the fractional diffusion aspects of models (space fractional diffusion equation and tempered fractional diffusion equations) before making investment decisions.

Example #2

A study on applications of the fractional diffusion equation in prediction of market behavior by Jonathan Blackledge.

A study was conducted to explore shortcomings associated with the Efficient Market Hypothesis or EMH in financial modeling systems, notably its failure to predict market volatility accurately. This study introduced a novel financial risk assessment model based on Lévy statistics, incorporating a solution to a non-stationary fractional diffusion equation characterized by the Lévy index.

Variations in the Lévy index were considered to forecast future volatility and assess market shifts. The study hypothesized that changes in the Lévy index preceded shifts in financial signals, offering insights into portfolio management. Results revealed a quantitative relationship between Lévy's characteristic function and a random scaling fractal signal derived from a Green's function solution to the fractional diffusion equation. This study, rooted in the Fractal Market Hypothesis, also presented a case study illustrating the prediction of volatility in foreign exchange markets.

Fractional diffusion equations use fractional derivatives to enhance accuracy in representing financial time series processes. They capture memory effects and long-range dependence on financial data. They are widely applied in finance and aid in asset price behavior analysis, volatility estimation, option pricing, and risk management.

These models can better depict financial market dynamics by integrating fractional derivatives, such as fractional Brownian motion and fractional Levy motion. Moreover, they advance quantitative finance and financial econometrics, offering valuable insights for researchers and practitioners.

The following general inferences can be drawn about the fractional diffusion models and their applications in finance:

• Impact on Option Pricing and Portfolio Behavior: These models significantly impact option pricing and influence portfolio behavior. They capture the complex dynamics present in financial markets, providing valuable insights into option valuation and portfolio responses to market changes.
• Memory Effects and Risk Redistribution: These models incorporate memory effects into market behavior, allowing for a more accurate representation of how past events influence current prices. They also consider risk redistribution mechanisms, providing a deeper understanding of how risks are spread and managed within portfolios.
• Insights into Volatility Dynamics: They offer insights into the dynamics of volatility, revealing how volatility changes over time and its impact on asset prices. By analyzing volatility patterns, these models enhance the understanding of market dynamics and support informed decision-making.
• Heavy-Tailed Probability Distributions: They excel in analyzing heavy-tailed probability distributions, which are crucial for understanding the occurrence of extreme events in financial markets. Furthermore, these models contribute to effective risk management and portfolio optimization by quantifying these distributions.
• Parameter Influence on Delta-Hedging Policies: Parameters within fractional diffusion models directly influence delta-hedging policies. These parameters impact how portfolios are constructed to mitigate changes in asset prices, affecting their sensitivity to market movements.
• Overall Framework for Market Analysis: These models provide a comprehensive framework for analyzing market conditions and guiding risk management strategies. Analysts can obtain a more precise representation of market conditions and volatility patterns, enabling more effective decision-making in portfolio management.