Statistical Significance

Statistical significance is the probability of an observation not being caused by a sampling error. It implies that the observation has a specific cause for it. Therefore, in order to consider an observation statistically significant, it has to clear the testing.

In order to prove statistical significance, the dataset has to reject the null hypothesis. To prove the null hypothesis wrong, the p-value of the observation should be less than the significance level. The p-value is the probability of an observation being caused by random factors.

• Statistical significance shows that observation is caused by a specific reason and not a random factor.
• The significance level is represented by α. The researcher ascertains its values and is usually 0.01, 0.05, or 0.1.
• The null hypothesis assumes that the research is false. However, an alternative hypothesis that is the researcher’s assumption can prove true, rejecting the null hypothesis.
• The conventional value of α = 0.05. Therefore, if the p-value for a dataset ≤ 0.05, then the result is statistically significant. If the p-value is> 0.05, then the research may not be statistically significant.

Statistical significance is widely applied as a quantitative research tool by researchers for decision making. This tool is applied in a variety of different fields such as business, marketing, advertising, investing, and finance.

The following two factors determine significance.

1. Sample Size: The number of observations immensely contribute to the level of significance. A large dataset (necessarily a randomized sample) often eliminates the sampling error.
2. Effect Size: The correlation between the two datasets or variables is termed effect size. A greater effect size, therefore, implies that two different studies show very similar values. Greater effect size indicates that the data is statistically more significant.

The alpha value (α) represents statistical significance. The traditional value of alpha is 0.05, which is 5%. It serves as a 95% threshold for the significance. It implies that the chance of result accuracy is 95%.

For achieving statistical significance, at least one of the given conditions should be fulfilled:

1. The p-value should be lower than the value of alpha.
2. The null hypothesis values should have no place in the confidence interval.

The confidence interval refers to the assured range in which the actual values fall. For a p-value of 0.05, that is 5%, the remaining 95% is considered the confidence interval.

For Example, in June 2020, ASPEN Trial did not achieve Statistical Significance on its primary endpoint. This was reported by Reuters.

The Statistical significance comprises finding the result and validating the result. The dataset has to successfully reject the null hypothesis.

#1 - Statistical Hypothesis Testing

A hypothesis is a researcher’s assumption. Researchers assume that they will get a particular result, even before conducting the test. This assumption is based on the relationship between the different variables or datasets.

The two types of hypothesis used for data analysis are as follows:

1. Null Hypothesis: Now, if the theory proposed by the researchers stands false, the researcher’s hypothesis is considered null. This is denoted by H0.
2. Alternative Hypothesis: However, if the researcher’s theory proves valid, it is referred to as the alternative hypothesis. This is denoted by H1.

#2 - Statistically Significant p-value

A p-value denotes probability value, which is the possibility of an outcome resulting from randomness or coincidence instead of facts. Thus, the level of statistical significance can be analyzed with the help of a p-value which ranges between 0 and 1. The statistical result is believed to be accurate when the p-value is equal to or less than 0.05. In other words, there is only a 5% chance that the data was caused by randomness or coincidence.

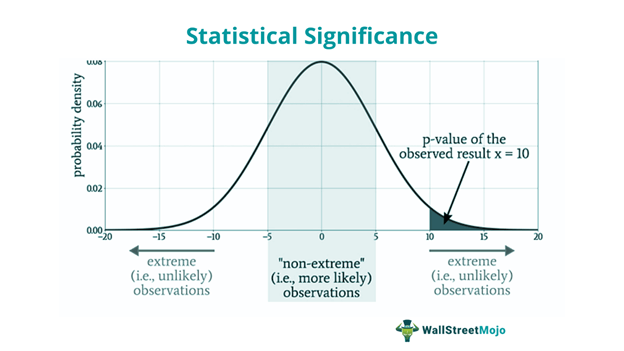
Therefore, the testing will result in the following two possibilities.

• p-value ≤ 0.05: A p-value equal to or smaller than 0.05 indicates that the null hypothesis is probably false. Thus, there are chances of the result being more statistically significant.
• p-value > 0.05: On the contrary, a value exceeding 0.05 signifies that the null hypothesis seems likely, and the result may not be statistically significant.

Consider the following problem based on a hypothetical scenario. Samuel, an amusement park owner, wants guests to spend more time in the park. The average time spent by 20 guests who visit the park is 199 minutes. Samuel decides to install new rides. For the test, the significance threshold is assumed at 5%, the sample mean is 200 minutes, and the standard deviation is 200 minutes. Based on the given data, conduct a significance test for Samuel.

Given Data:

• µ = 199 minutes
• n = 20
• µ remains 199 minutes before installing new rides
• µ > 199 minutes after installing new rides
• α = 5% or 0.05
• x̄ = 200 minutes
• σ = 200 minutes

Calculation

We will be applying the z-test here,

Z = (x̄ - μ) / √(σ2 / n)

Z = (200 - 199) / √(200 / 20)

Z = 1 / 3.16228

Z = 0.31623 = 0.3

Now let’s determine the z-score or the p-value on the given z-table:

Thus, the p-value is 0.51197.

Here, p-value > α, i.e., 0.51197 > 0.05

Therefore, the null hypothesis can be true, and the result is not statistically significant.

Users can alternatively select from various calculators available online to conduct significance tests.

Statistical significance rules out random coincidence and indicates that the data is a result of a specific cause. However, practical significance finds out the magnitude of that effect and its relevance in the real world.

While researchers use sample size and p-value for ascertaining statistical significance, the effect size of the datasets indicates practical significance.

Thus, acquiring statistical significance without determining the practical significance would not be very helpful.

This has been a Guide to Statistical Significance and its Meaning. Here we discuss the significance tests (p-value) and how to understand its levels along with examples and calculations. You may also have a look at the following articles to learn more –

• Hypothesis Testing
• Degrees of Freedom
• Chi-Square Test in Excel