Table Of Contents
What is Marginal Rate of Substitution?
The marginal rate of substitution (MRS) is the rate at which some units of an item can be replaced by another while providing the same level of satisfaction to the consumer. The MRS concept describes the relationship between the consumption of two goods or resources when consumers make rational decisions.
- The marginal rate of substitution indicates the balance achieved between two desirable goods or resources without compromising the utility.
- MRS forms a part of the indifference curve theory, which measures how consumers react to different goods to get the same level of satisfaction.
- The formula for calculating the MRS = Change in good y/Change in good x
- Also, the graphical representation of the MRS involves drawing out an indifference curve involving the two products.
- The theory comes with limitations as the application is restricted to two commodities.
How Does Marginal Rate of Substitution Work?
In consumer behaviour research, learning how to calculate the marginal rate of substitution is fundamental. Usually, consumers make rational decisions when there is a resource scarcity or financial constraint. Therefore, the MRS evaluates consumer behavior in such situations. For instance, you may be hungry but lack the financial means to purchase the commodity in the desired quantity. Although, for the same amount of money, you may fulfill your appetite with the same level of satisfaction by swapping a portion of the amount desired with similar food.
Consider the following example:
Customer A wanted to buy dates for making dates tea cake. However, she couldn't find the required quantity of dates at the nearest store, so she substituted the remaining quantity with raisins.
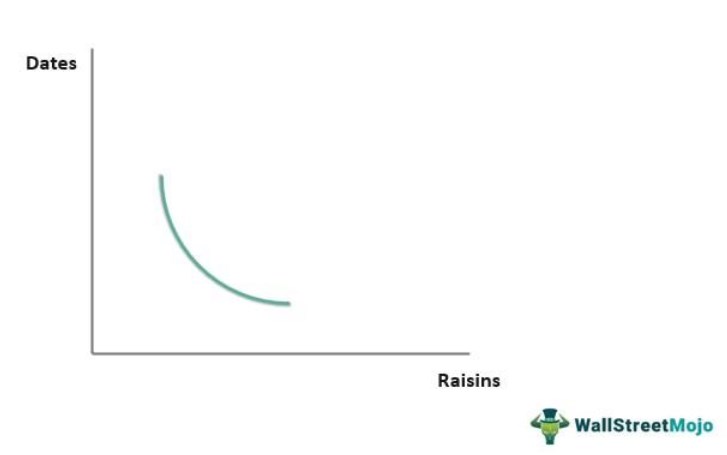
In the above graph, the indifference curve highlights the points representing different combinations of dates and raisins that may be brought and used to make the tea cake. Each combination will bring the same level of satisfaction and utility.
How is the MRS Represented?
Economists use a graph to analyze and explain the MRS. The value of the MRS is equal to the slope of the indifference curve drawn for the two products. For example, in the above graph of dates and raisins, the points on the indifference curve disclose the different combinations of the two products yielding similar satisfaction. The graph is downward sloping and convex to the origin.
We can depict more than one indifference curve for two products, but combinations that lie on different curves have varying usefulness. For example, when compared to combinations on lower indifference curves, combinations on higher indifference curves offer more utility.
Types of indifference curves vary with the nature of goods.
|
Types of indifference curve |
||||
| Diminishing | Normal goods (imperfect substitutes) | Convex to the origin | One good increases and the other one decreases | MRS decreases |
| Constant | Perfect substitutes | Straight lines | Maintains a 1:1 ratio | MRS is constant |
| Increasing | Perfect compliments | L shaped indicating a right angle | Increase in both products | MRS is either infinite or zero |
Diminishing Marginal Rate of Substitution
Under the diminishing rule, the increase in one resource gets balanced by a decrease in the other resource. For representing a diminishing MRS, assumptions portrayed are:
- The indifference curve never touches both axis of the graph
- Two indifference curves never intersect
- The indifference curve is downward slopping
- The indifference curve is convex to the origin indicating that MRS is diminishing
- The substitutes are never perfect substitutes or perfectly complementing in nature. Rather they should be normal goods with substitutable properties.
- We will not increase the number of both products simultaneously; rather, the changes in quantity will be in opposing directions.
Marginal Rate of Substitution Formula

Calculation of MRS:
We can use the following steps to derive MRS.
MRS of good x for good y= change in good Y/change in good X
- X: Represents the substitute
- Y: Existing or current resource getting replaced
Marginal Rate of Substitute Formula = △Y/△X
where,
- △Y Change in Good Y
- △X Change in Good X
The MRS formula shows that when the number of substitutes grows in the subsequent phases and the number of current resources decreases, the MRS falls.
MRS representation in terms of marginal utility.
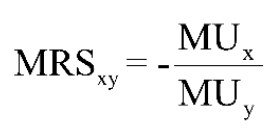

Limitations
The main limitation of this theory is that it correlates to only two products at a time. Thus, for instance, we can calculate the MRS of good A for good B, good A for good C, and good B for good C, but it cannot portray a combination of A, B and C.
To get the result, you would need to calculate the MRS three times by discovering how:
- Item A relates to item B.
- Item A relates to item C.
- Item B is related to item C.
Example
A basic understanding of the MRS helps retailers make efficient product assortment and attain target sales.
Customer A went to a confectionery store with a high product mix to purchase baked goodies. He planned to buy 13 pieces of pastries and one cupcake. However, he ended up buying more of the cupcake since he couldn't find the necessary number of pastries. The customer replaced desired option with another one because it was out of stock at the moment of the purchase.
| Combination or Bundle | Cupcake | Pastries | MRS= Ratio: Δy/ Δx |
|---|---|---|---|
| A | 1 | 13 | |
| 2 | 9 | -4 or 4:1 | |
| C | 3 | 7 | -2 or 2:1 |
| D | 4 | 6 | -1 or 1:1 |
MRS = Change in Pastries/Change in Cupcake
= Δy/ Δx
= slope of the indifference curve
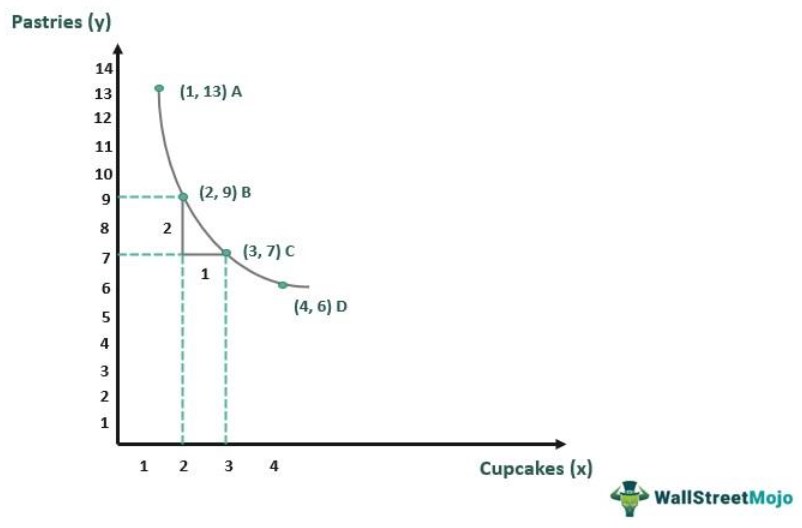
- Bundle A contains thirteen pieces of pastries and one cupcake.
- Bundle B contains nine pastries and two cupcakes. Sacrifices four pastries for an additional cupcake.
- Bundle C contains seven pastries and three cupcakes. Sacrifices two pastries for an additional cupcake.
- Bundle D contains six pastries and four cupcakes. Sacrifices one pack of pastries for an additional cupcake.
Bundles A, B, C, and D all give the same level of enjoyment. Thus, we may also deduce that in the beginning, the customer was ready to make concessions and substitute a greater quantity of pastries with the cupcake.
We can observe that the number of pastries replaced reduces in the following combinations. As such, this example shows that the marginal rate of substitution is diminishing.
FAQs
MRS formula:
MRS of X for Y

Marginal utility is the additional satisfaction generated by having additional units. It relates to the satisfaction beyond normal consumption.
Marginal rate of substitution interprets the balance achieved between primary item and substitutes during selection process or at the time of purchase.
Example: Customer intended to buy three shirts but purchased two T-shirts and one pair of pants. The customer gave up purchasing an additional T-shirt in order to acquire one pair of branded jeans that he was drawn to.
Recommended Articles
This has been a guide to what is Marginal Rate of Substitution is. Here we discuss its definition, formula, limitations, how it works, examples, diminishing marginal rate of substitution. You can learn more about accounting from the following articles –
