Rho in Options

What Is Rho In Options?

Rho in options refers to the metric  used for assessing the sensitivity of an option to the changes in the risk free interest rate. It is particularly useful only when the interest rate changes dramatically, and this is the reason that it is not part of the vast majority of options trading strategies.

It is one of the least used Greek option metrics as the option price is not significantly impacted due to a change in interest rates. The rest three Greek metrics used include alpha, gamma, vega, and theta. It, in addition, acts as one of the factors to determine the risk exposure of an investment.

• Rho is a Greek letter used in options trading to measure the sensitivity of the option price to changes in interest rates. 
• It indicates how much the option price is expected to change for a one-percentage-point change in the risk-free interest rate.
• Rho is particularly relevant for options, as interest rates affect the present value of future cash flows. Call options generally have a positive rho, indicating that their value increases with higher interest rates. In contrast, put options typically have a negative rho, as their value decreases with higher interest rates.

Rho In Options Explained

Rho in options shows the amount of money that an option would either gain or lose in case the risk-free interest rate changes by 1%. In the US, the interest rate for US Treasury bills is used as the proxy for risk free interest rate. Typically, Rho is expressed in terms of dollar amount.

Figuring out the Rho helps investors and traders learn about the risk associated with a particular portfolio. As a result, they prepare a backup plan beforehand to tackle if the situation runs out of control.

The exact formula for Rho can be expressed in a very complicated way, wherein it is calculated as the first derivative of the value of the option relative to the risk-free interest rate. However, in a simpler way, the formula for Rho can also be expressed by using the spot price, option strike price, normal cumulative distribution function, risk-free interest rate, standard deviation, and time to option's expiry.

Types

Rho in options is broadly classified into two categories:

Positive Rho

If all other factors remain the same, then the value of an option with positive Rho will increase with the increase in interest rates and decrease with the fall in interest rates fall.

Negative Rho

If all other factors remain the same, then the value of an option with negative Rho will decrease with the increase in interest rates and increase with the fall in interest rates fall.

Formula

Mathematically, it is represented as,

ρ = K * t * e^−r*t * N(d₂)

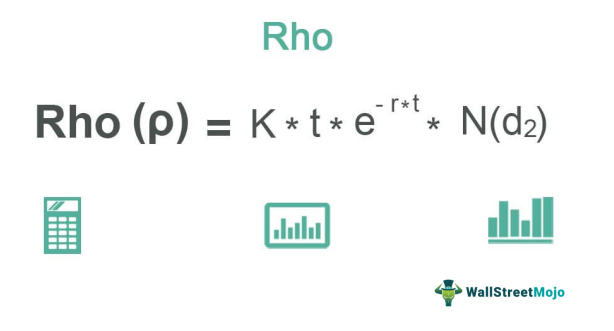
where, d₁ = σ√t

d₂ = d₁ − σ√t

• S = Spot price
• K = Option strike price
• N = Normal cumulative distribution function
• r = Risk-free interest rate
• σ = Standard deviation
• t = time to option's expiry

Graph

Let us understand the concept better with the help of a graph.  

Suppose an individual prices a call option showing a .25 Rho value with a 2.50 theoretical value. In case the interest rates jump to 6% from 5%, the call option’s price will be subject to a .25 increase to 2.75, at least from a theoretical standpoint. 

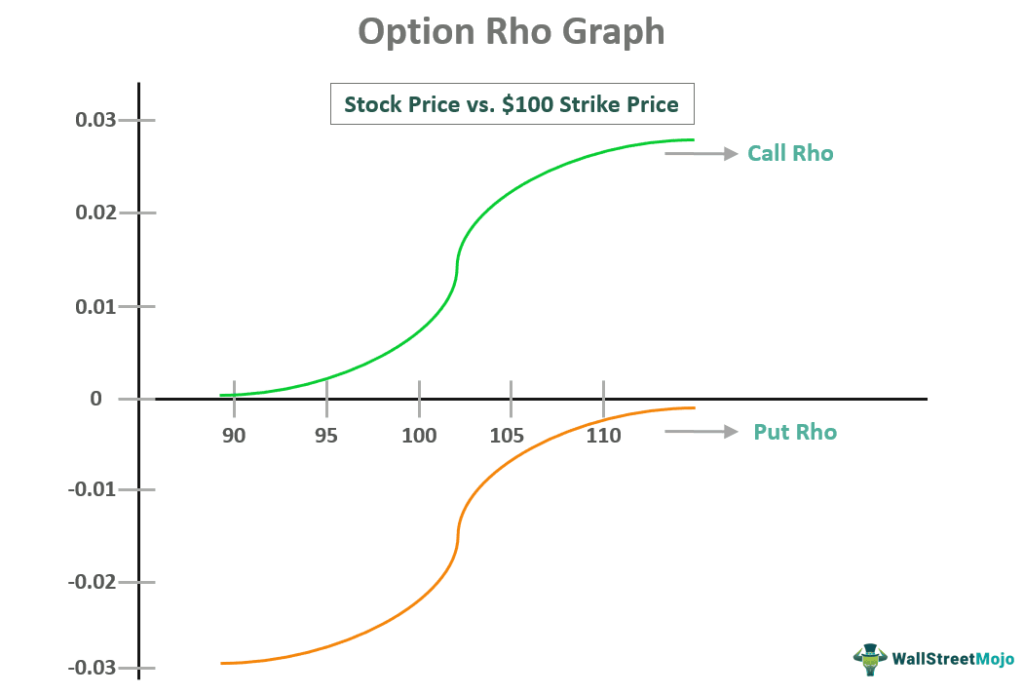
As one can observe from the graph given above, the option rho for puts and calls featured a mirrored profile. As the asset price rises, the calls move to a positive figure from 0. On the other hand, in the same situation, puts move toward 0 from a positive figure. That said, one must keep in mind that Rho is less about underlying price movements and more about movements concerning interest rates. Thus, one can observe greater effects of its value on the basis of the option premium. 

Examples of Rho

Let us consider the following examples to understand how Rho affects options trading:

Example #1

Let us take a simple example to illustrate the concept of Rho. Imagine that there is a call option priced at $5.00, and it has a rho equivalent of $0.50. Now, if the risk-free interest rate increases by 0.5% (from 2.5% to 3.0%), then what will be the impact on the value of the call option?

Theoretically, every 1% increase in an interest rate should increase the value of the call option by $0.50. In this case, the interest rate increased by 0.5%, so the value of the call option should increase by $0.25 (= 0.5%/1% * $0.50). So, the new value of the option would be $5.25.

Example #2

Let us take another example of a put option to explain the computation of Rho in more detail. In this case, the spot price of the underlying is $45, the strike price is $50, the risk-free interest rate is 1%, and the standard deviation is 0.25. Determine the Rho of the option is the time to option’s expiry is one year.

Given,

• The option strike price, K = $50
• Spot price, S = $45
• Risk-free interest rate, r = 1%
• Standard deviation, σ = 0.25
• Time to option's expiry, t = 1 year

Solution

Now, the value of d₁ and d₂ can be calculated as,

d₁ = σ√t

• = 0.25√1
• = -0.2564

d₂ = d₁ − σ√t

• = -0.2564 -  0.25√1
• = -0.5064

Now, the Rho of the option can be calculated by using the above formula as:

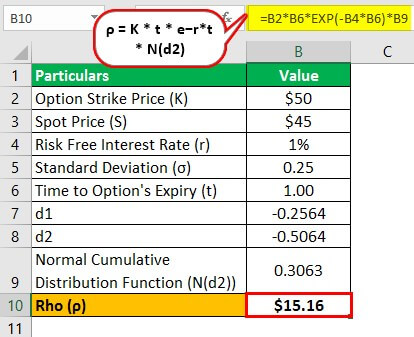
• = $50 * 1 * e^−1%*1 * N(-0.5064)
• Rho = $15.16

Therefore, for every 1% change in the interest rate, the value of the put option will increase by $15.16.

Conditions

The three major option conditions with respect to Rho are as follows -

1. Out-of-the-Money (OTM) - An Out of the Money option can either be a put option for which the strike price is lower than the spot price or a call option for which the strike price is higher than the spot price. Typically, out-of-money options exhibit a very low value of Rho.
2. At-the-Money (ATM) - The strike price of At the Money option is the same as the spot price of the underlying asset. If both call and put options are simultaneously at-the-money, then both may increase in value provided there is huge uncertainty about the underlying stock’s future price. In such cases, the value of Rho of call and put option decides which way the market perceives the underlying stock’s future price movement. Typically, at-the-money options exhibit a higher value of Rho.
3. In-the-Money (ITM) - An In the Money option can either be a call option for which the strike price is lower than the spot price or a put option for which the strike price is higher than the spot price. Typically, in-the-money options exhibit a higher value of Rho.

Uses

Though Rho is an indispensable part of the Black–Scholes options-pricing model, it is regarded as one of the least used Greek option metrics. This is because for Rho to have a significant impact on the price of an option; the interest rate has to change drastically, which is usually not the case.

Frequently Asked Questions (FAQs)

Recommended Articles

This has been a guide to what is Rho In Options. Here we explain it with a formula, examples to show calculation, types, conditions, and uses. You may learn more about financing from the following articles –

• Options Spread
• Currency Options
• Stock Options
• Knock-Out Option