Black Scholes Model

The Black-Scholes model determines a stock's theoretical price in options trading. It is used for both call and put options. The model relies on five variables for price calculation: underlying asset's price, strike price, risk-free rate, volatility, and expiration time. It is only applicable to European options trading.

The Black-Scholes theory was developed by economists Fischer Black and Myron Scholes in 1973. It is the most common options trading model and binomial model. The model is based on many assumptions limiting its usage outside European options trading.

• Black-Scholes is a pricing model used in options trading. It derives the fair price of a stock.
• Fischer Black and Myron Scholes met at the Massachusetts Institute of Technology (MIT). Their pricing model completely revolutionized technical investing. Black and Scholes won the Nobel prize for their contribution in 1997.
• Black and Scholes assume that there are no market arbitrage opportunities or riskless profits. In real-world scenarios, volatility is not constant across time; transaction costs exist.
• Real-world data depicts that price returns tend to have a skewed distribution; prices fall much faster than they rise.

The Black-Scholes Model was developed by economists Fischer Black and Myron Scholes in 1973. The Black-Scholes model works on five input variables: underlying asset's price, strike price, risk-free rate, volatility, and expiration time.

It is a mathematical model that utilizes a partial differential equation to calculate the price of options. This partial differential is known as the Black-Scholes equation. Banks and financial institutions use this model for evaluating European options. The primary objective behind the model is to hedge options in a portfolio and eliminate the risk factor.

Fischer Black and Myron Scholes met at the Massachusetts Institute of Technology (MIT) and started a partnership that lasted 25 years. Their pricing model completely revolutionized technical investing. Black and Scholes won the Nobel prize for their contribution in 1997.

Black and Scholes assume there are no market arbitrage opportunities or riskless profits. This is why the model receives criticism. In real-world scenarios, volatility is not constant across time; transaction costs exist. Real-world data depicts that price returns tend to have a skewed distribution; prices fall much faster than they rise.

At the beginning of the 20th century, French mathematician Louis Bachelier made an analogy between Brownian motion and the movement of financial assets in his Theory of Speculation. The Black-Scholes theory incorporates this assumption.

Black-Scholes model assumptions are as follows.

• Black-Scholes theory assumes that option prices exhibit Brownian motion.
• The model assumes that risk-free rates are constant. In reality, they are dynamic—they fluctuate with supply and demand.
• The theory assumes stock returns resemble a log-normal distribution.
• It also assumes that we have a frictionless market; that there are no transaction costs, which is not the case with real-world scenarios.
• Black and Scholes neglect dividend payouts throughout the option period.

The Black-Scholes model formula is as follows:

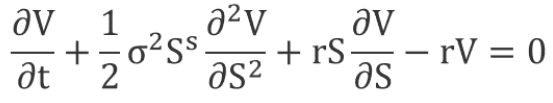
The above equation determines the stock options price over time.

The following formula computes the price of a call option C:

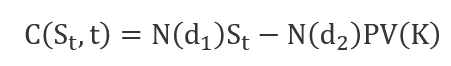
Here,

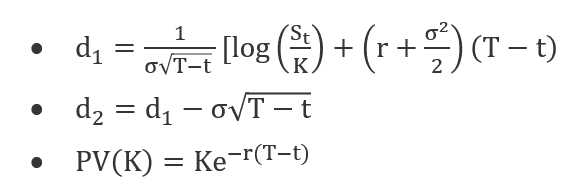
The following formula computes the price of a put option P:

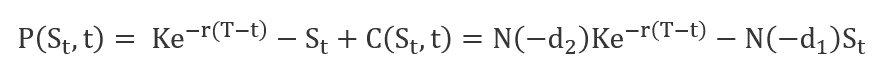
• In this equation, N equals the cumulative distribution function of the standard normal distribution. It represents a standard normal distribution with mean = 0 and standard deviation = 1

• T-t refers to the maturity period (in years).
• St is the underlying asset's spot price.
• K denotes the strike price.
• r represents the risk-free rate.
• Ó symbolizes the underlying assets' return volatility.

Now, let us look at a Black-Scholes model example to understand calculations.

To estimate the value of a call option for Apple (AAPL), the following formula is used:

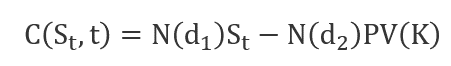
Here,

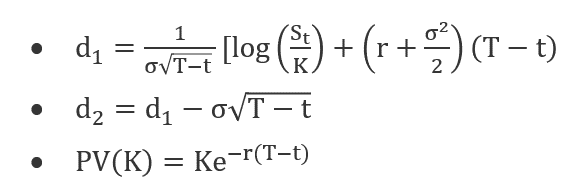
On October 17, 2022, the call option for Apple’s stock ($AAPL) was priced at S = $138.38 (on NASDAQ).

We multiply the current price by 1.2 to determine an exercise price 20% higher than the current stock trading price of X = $166.05.

Further, we take a 101-day expiration period (ends January 25, 2023) and consider a risk-free interest instrument, $USGG10YR, that pays 2.12% currently. It is a US 10-year government bond.

Therefore, the values are as follows:

• S = 138.38 (Stock Price)
• X = 166.05 (Trading Price)
• (T-t) = 101 (Expiration Period)
• r = 0.0212. (Risk-Free Rate)

The only parameter missing is the stock volatility estimation. It can be determined using historical prices. If the resulting value, σ, varies between 0 and 1, it represents the market’s implied stock volatility.

The stock's fair price helps traders hedge their portfolios; they eliminate the risks.

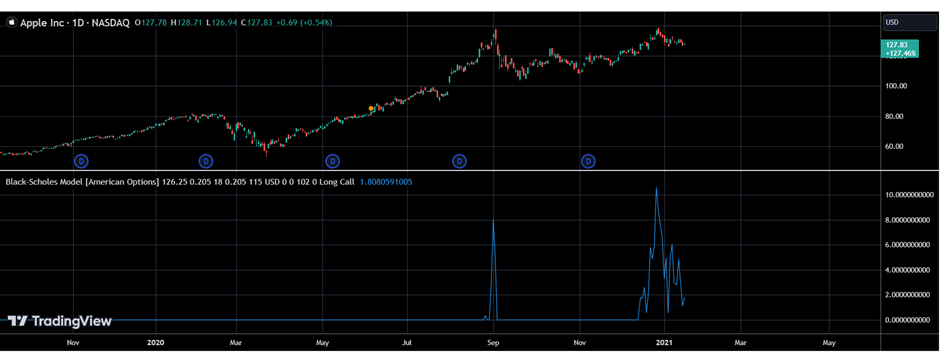
It is possible to explain the model with the help of a chart taken from TradingView, in the chart given below, related to Apple Inc., where the model has been used. There are some steps followed in the process. Some data, like the strike price, the risk-free rate, and the dividend yield, are entered. Then, the time duration till the ex-dividend date is entered along with the time till expiry. Finally, to create the chart, the trader has to enter the time frame of the chart in minute terms. Then, they need to select what kind of option they want to go for.

It is to be noted that this kind of model is more suitable for stocks. Therefore, it is advisable to use it for stocks. It is also important to know that the variables related to the time factors will not update by themselves. The trader will have to change them everyday.

Source

The importance of the Black-Scholes model is as follows:

• It is a prominent option pricing model, in addition to the binomial model.
• Traders and analysts use it to determine the fair value of a stock.
• Using this model, investors or traders can hedge their position with minimum risks.
• Options trading is an advanced form of investment and market study. The Black-Scholes method plays a key role in determining the price.

• The model works only on European options, not on US options.
• The pricing of in-the-money options is accurate, but deviations are high for out-of-money options.
• The model can estimate volatility only when other factors are calculated. This reliance makes the model limiting.  
• The model assumes the same condition, irrespective of the application. For example, it assumes a frictionless market.

Problems associated with the unrealistic Black-Scholes assumptions have been solved using partial derivatives— Option Greeks.

Black-Scholes is a multivariate equation; institutional traders want to understand how each variable functions in terms of other variables in isolation. It allows traders to strip down financial risks into several types that can be properly managed and hedged.

The most common Option Greeks are delta, gamma, theta, vega, and rho. Each parameter measures one specific type of risk associated with an option position. The delta measures exposure to the directional risk. Similarly, the gamma measures the exposure to price fluctuations in either direction. And the theta measures the exposure to the passage of time.

On the other hand, Vega measures the exposure to changes in implied volatility. Rho measures the exposure to changes in the risk-free interest rates.

Now, institution traders do not trade based on price direction. Instead, they use the Black-Scholes method and its partial derivatives to determine price volatility. Option price volatility is easier to determine than price direction since it is mathematical.

This article has been a guide to what is the Black-Scholes Model & its meaning. We explain its assumptions, formula, examples, importance, and limitations. You can learn more about it from the following articles -

• Option Pricing
• Volatility Index
• Option Selling