Table Of Contents
Simple Random Sampling Definition
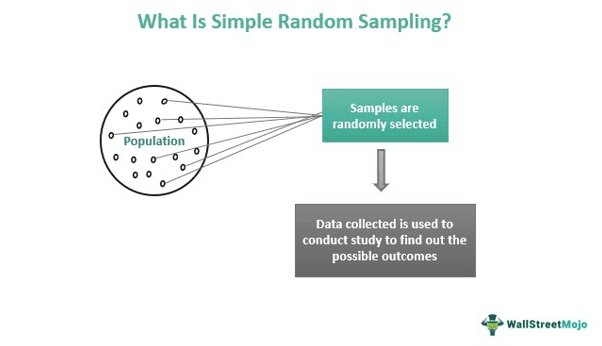
Simple random sampling is the method of randomly selecting samples from a population based on the type and nature of the study. Researchers use this technique of studying a social group to find out the possibility of an outcome. The results, in turn, become a ready reference for analysts who can easily predict outcomes in the events having similar traits.
It is one of the types of random sampling, with stratified, systematic, and cluster random sampling being the other three. As researchers choose the samples randomly, they are unbiased. However, this randomness might not help users collect appropriately segmented preferences of the population all the time.
Key Takeaways
- Simple random sampling is when users randomly select a subset of a population, who become the samples for the study to be conducted.
- The methods of sample selection are – the lottery method and the random number generation.
- This method of random sampling is opted for when researchers or analysts have the complete list of members in the population.
- Sampling error is likely to occur as the data collected may not match the sample requirements perfectly.
How Does Simple Random Sampling Work?
Simple random sampling is the random selection of individuals/units representing a particular population. In the process, every entity or individual has similar chances of being selected as a random sample for a study. Choosing random samples ensures unbiased selection, guaranteeing the outcome would represent the entire population and not individuals with specific traits.
For this method of sampling to be effective, researchers or analysts must have a list of all the members of the society/population. There are always chances of errors when users choose simple random samples. Researchers may end up choosing samples that might be an accurate representation of a particular portion only and not the entire population.
This plus or minus variance leads to sampling error, affecting the entire study and leading to misleading inferences. When users have a list of all members of the population to be studied, the chances of errors reduce. However, it is not possible to track every single unit of the population. As a result, the inference or conclusion turns unreliable.
To note here is that the more the number of samples, the better and more accurate the results are.
Simple Random Sampling Techniques
There is no simple random sampling formula to select the subset for conducting a study. Instead, users consider using two methods for conducting random sampling – the lottery method and random numbers usage.
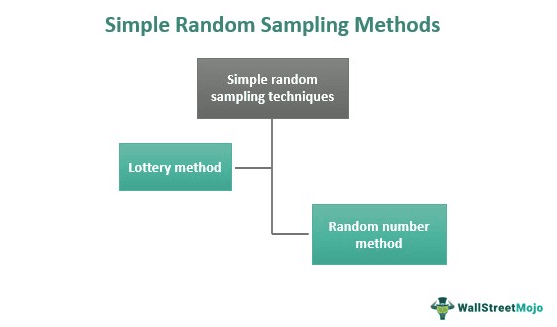
The lottery method is the oldest simple random sampling method where users assign each object in the population a number to follow systematically. They write the numbers on paper and mix the chits in a box. Users take out the chits randomly from the box, and whatever number they contain, participants with that assigned number become the samples for the study.
In random numbers method, each member of a population has a number in a random pattern arranged in a tabular form. At the time of sampling, each number has an equal chance of selection as sample from the table. Nowadays, software products help conduct this random sampling for a more accurate study.
Example
Let us consider the following simple random sampling example to understand how the sampling process works:
Suppose Company X, with 1000 employees all across, wants to find out the workspace preferences of its employees to decide whether to continue calling them to the office or allow them work-from-home or have a hybrid working space. So, the software prepares a list of staff members and assigns specific numbers to each of them, from 1-1000.
The research team decides selecting 300 samples from the available number of employees. The software randomly selects 300 people from the list, and they become the samples for the study. Based on their responses, the company can proceed with the form of working space they should allow their employees.
Advantages & Disadvantages
Though there are many advantages of simple random sampling, the concept is not devoid of disadvantages. Let us have a look at the benefits and drawbacks of the sampling process:
| Pros | Cons |
|---|---|
| Fair and unbiased as each member of the society has equal chances of being selected as a sample | Unrestricted sample selection might make the sampling process less efficient. |
| Picking a smaller portion of a population is easier | Time-consuming as there is a large volume of data collected |
| Sample size is unrestricted | Expensive |
| No restriction on the types of samples to be chosen |
Simple vs Stratified, Cluster, Systematic Sampling
Random sampling is of four types. While simple random samples include subsets with no specific trait, stratified sampling involves choosing samples based on specific criteria or types. For example, studying the population between 40-60 years to determine the investment options they would choose to safeguard their future financially.
While users choose simple random samples to know who they want as their sample, they prefer cluster sampling when they cannot find the samples they want. In such a scenario, they might divide the whole population into clusters or groups and choose samples that best define or represents the type of sample required for the study or research.
Researchers opt for simple random samples when they already have the complete list of members in the population. On the contrary, systematic sampling is all about choosing samples at regular intervals, especially when users do not have a complete list of the population.
