Sampling Distribution Formula

What is the Sampling Distribution Formula?

A sampling distribution can be defined as the probability-based distribution of particular statistics and its formula helps in calculation of means, Range, standard deviation and variance for the undertaken sample. S

For a sample size of more than 30, the sampling distribution formula is given below –

Here,

• The mean of the sample and population are represented by µ͞x and µ.
• The standard deviation of the sample and population is represented as σ_͞x and σ.
• The sample size of more than 30 represents as n.

Explanation

You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Sampling Distribution Formula (wallstreetmojo.com)

Examples of Sampling Distribution Formula (with Excel Template)

Let’s see some simple to advanced practical examples of the sampling distribution equation to understand it better.

Example #1

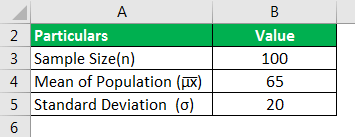
Let us take the example of the female population. The size of the sample is at 100, with a mean weight of 65 kgs and a standard deviation of 20 kg. Help the researcher determine the mean and standard deviation of the sample size of 100 females.

Solution

Use below given data for the calculation of sampling distribution

The mean of the sample is equivalent to the mean of the population since the sample size is more than 30.

Calculation of standard deviation of the sample size is as follows,

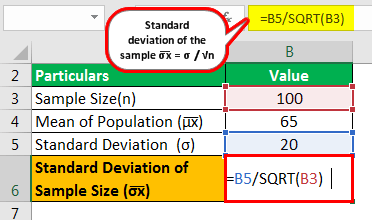
• =20/√100

Standard Deviation of Sample Size will be –

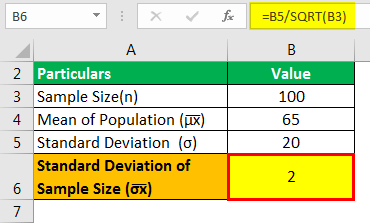
• σ_͞x =2

Therefore, the standard deviation of the sample is 2, and the mean of the sample is 65 kg.

Example #2

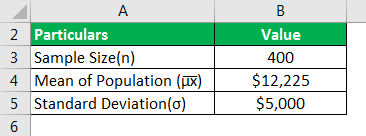
Let us take the example of taxes paid by the vehicles. In the state of California, the average tax paid is $12,225 having a standard deviation of $5,000. Such observations were made on the sample size of 400 trucks and trailers combined. Help the transport department to determine the mean and standard deviation of the sample.

Solution

Use below given data for the calculation of sampling distribution

Calculation of standard deviation of the sample size is as follows,

• = $5,000 / √400

Standard Deviation of Sample SizeSample SizeThe sample size formula depicts the relevant population range on which an experiment or survey is conducted. It is measured using the population size, the critical value of normal distribution at the required confidence level, sample proportion and margin of error.read more will be –

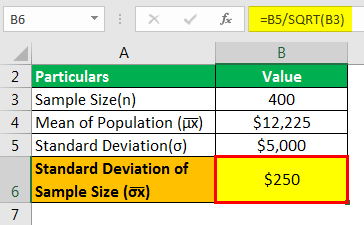
• σ_͞x =$250

Therefore, the standard deviation of the sample as assessed by the department of transport is $250, and the mean of the sample is $12,225.

Example #3

Let us take the example of the following data is displayed below:

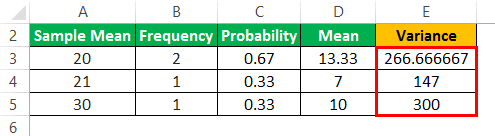
Sample Mean	Frequency	Probability
20	2	0.67
21	1	0.33
30	1	0.33

Help the researcher determine the mean and standard deviation of the sample.

Determine the mean of the sample as displayed below: –

• =20*0.67

Mean will be –

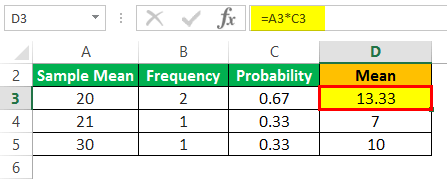
• =13.33

Total Mean

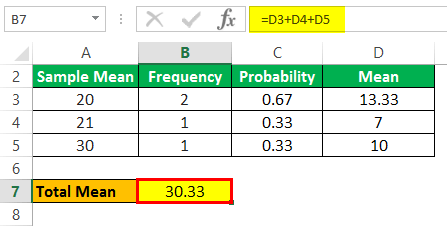
• =13.33+7+10
• Total Mean =30.33

Determine the variance of the sample as displayed below: –

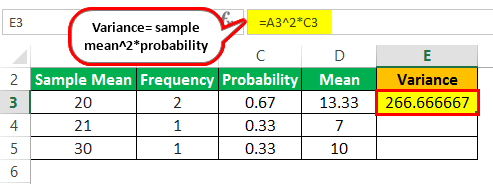
• =20^2*0.67
• =266.66667

Variance 

Total Variance

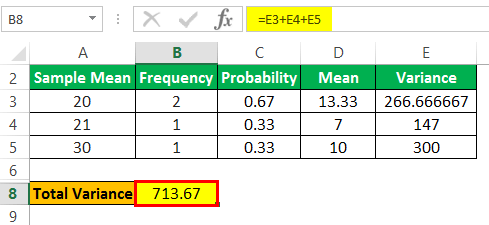
• = 713.67

Calculation of standard deviation of the sample size is as follows,

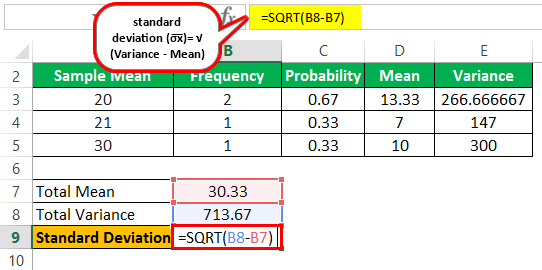
• σ_͞x = √ 713.67 – 30.33

Standard Deviation will be –

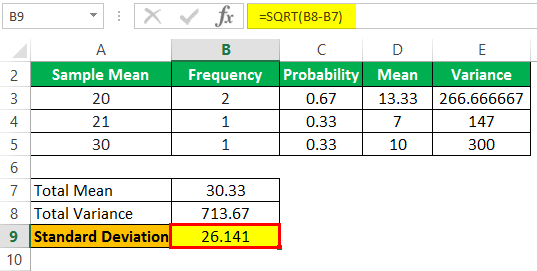
• σ_͞x = 26.141

Therefore, the standard deviation of the sample, as assessed by the researcher, is 26.141, and the mean of the sample is at 30.33.

Relevance and Use

The sampling distribution is utilized by many entities for the purpose of research. It could be analysts, researchers, and statisticians. Whenever the population size is large, such methodology helps in the formulations of the smaller sample, which could then be utilized to determine average means and standard deviations. The average means can be plotted on the graph to arrive at the uniform distributionUniform DistributionUniform Distribution is a probability distribution type where every probable outcome has the same possibility of occurrence & it is further categorized into Continuous & Discrete Distribution. This is represented as a straight horizontal line. read more relating to the population, and if the researcher increases the sample size, the probability of the graph reaching normal distribution enhances.

It helps in major simplification of the inferences taken up in statistics. It further helps in deducing analytical contemplation by determining the frequency of the probability distributionProbability DistributionProbability distribution is the calculation that shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as required. It is a mathematical function that gives results as per the possible events.read more of sample means. The sampling distribution forms base for several statistical concepts that may be used by the researchers to facilitate their hypothesis.

Recommended Articles

This has been a guide to Sampling Distribution Formula. Here we discuss how to calculate the sampling distribution of standard deviation along with practical examples and a downloadable excel sheet. You can learn more from the following articles –

• Attribute Sampling
• What is Conditional Probability?
• Poisson Distribution in Excel
• Log Normal Distribution Definition
• Exponential Distribution