Sample Size (Definition, Formula) | Calculate Sample Size

Formula to Determine Sample Size of Population

Sample Size Formula helps in calculating or determining the minimum sample size which is required in order to know the adequate or correct proportion of the population along with the confidence level and the margin of error.

The term “sample” refers to the portion of the population that enables us to draw inferences about the population and so it is important that the sample size is adequate enough so that meaningful inferences can be made. In other words, it is the minimum size that is needed to estimate the true population proportion with the required margin of error and confidence level. As such, the determination of the appropriate sample size is one of the recurrent problems in statistical analysis. Its equation can be derived by using population size, the critical value of the normal distribution, sample proportion, and margin of error.

where,

N = Population size,
Z = Critical value of the normal distribution at the required confidence level,
p = Sample proportion,
e = Margin of error

How to Calculate Sample Size? (Step by Step)

Step 1: Firstly, determine the population size which is the total number of distinct entities in your population and it is denoted by N. [Note: In case, the population size is very large but the exact number is not known, then use 100,000 because the sample size doesn’t change much for populations larger than that.]
Step 2: Next, determine the critical value of the normal distribution at the required confidence level. For example, the critical value at 95% confidence level is 1.96.
Step 3: Next, determine the sample proportion which can be used from previous survey results or be collected by running a small pilot survey. [Note: if unsure one can always use 0.5 as a conservative approach and it will give the largest possible sample size.]
Step 4: Next, determine the margin of error which is the range in which the true population is expected to lie. [Note: Smaller the margin of error, more is the precision and hence the exact answer.]
Step 5: Finally, the sample size equation can be derived by using population size (step 1), the critical value of the normal distribution at the required confidence level (step 2), sample proportion (step 3) and margin of error (step 4) as shown below.

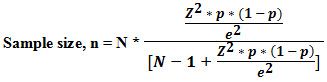
Examples

You can download this Sample Size Formula Excel Template here – Sample Size Formula Excel Template

Example #1

Let us take the example of a retailer who is interested to know how many of their customers bought an item from them after viewing their website on a certain day. Given that their website has on average 10,000 views per day, determine the sample size of the customers that they have to monitor at a 95% confidence level with a 5% margin of error if:

They are uncertain of the current conversion rate.
They know from previous surveys that the conversion rate is 5%.

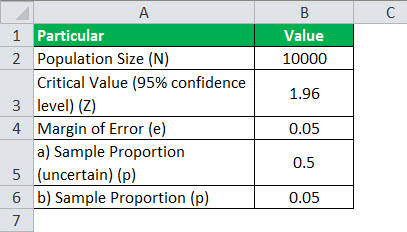
Given,

Population size, N = 10,000
Critical value at 95% confidence level, Z = 1.96
Margin of error, e = 5% or 0.05

1 – Since the current conversion rate is unknown, let us assume p = 0.5

Therefore, the sample size can be calculated using the formula as,

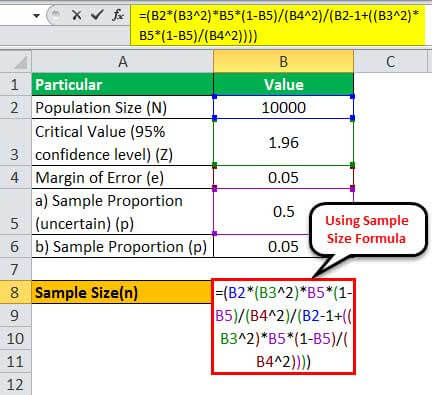
= (10,000 * (1.96 ²)*0.5*(1-0.5)/(0.05 ²)/(10000 – 1+((1.96 ²)* 0.5*(1-0.5)/(0.05 ²))))

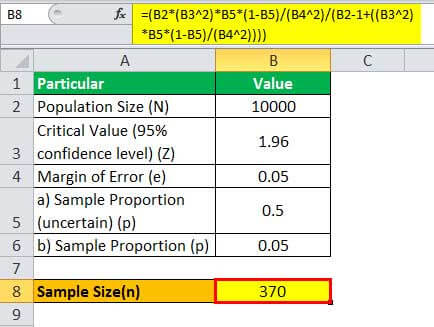
Therefore, 370 customers will be adequate for deriving meaningful inference.

Popular Course in this category

All in One Financial Analyst Bundle (250+ Courses, 40+ Projects)4.9 (1,067 ratings) 250+ Courses | 40+ Projects | 1000+ Hours | Full Lifetime Access | Certificate of Completion

View Course

2 – The current conversion rate is p = 5% or 0.05

Therefore, the sample size can be calculated using the above formula as,

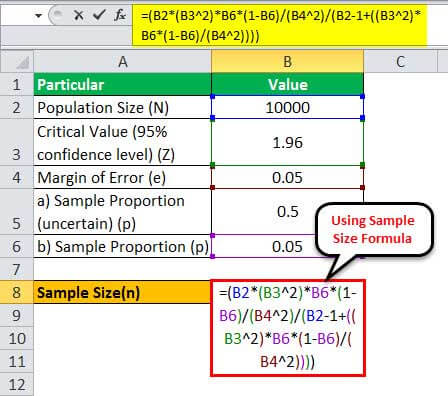
= (10,000 * (1.96 ²)*0.05*(1-0.05)/(0.05 ²)/(10000 – 1+((1.96 ²)* 0.05*(1-0.05)/(0.05 ²))))

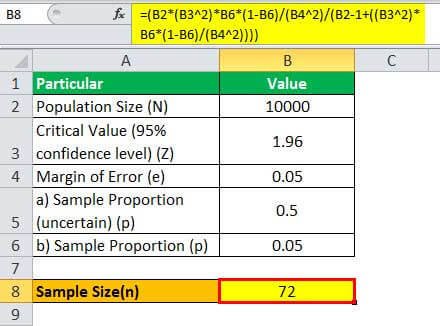
Therefore, a size of 72 customers will be adequate for deriving meaningful inference in this case.

Example #2

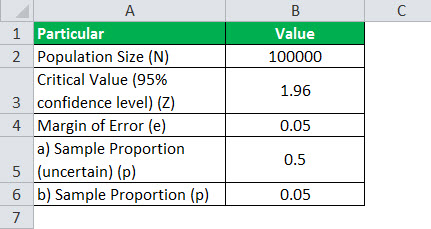
Let us take the above example and in this case let us assume that the population size, i.e. daily website view, is between 100,000 and 120,000, but then the exact value is not known. The rest of the values are the same along with a conversion rate of 5%. Calculate the sample size for both 100,000 and 120,000.

Given,

Sample proportion, p = 0.05
Critical value at 95% confidence level, Z = 1.96
Margin of error, e = 0.05

Therefore, the sample size for N = 100,000 can be calculated as,

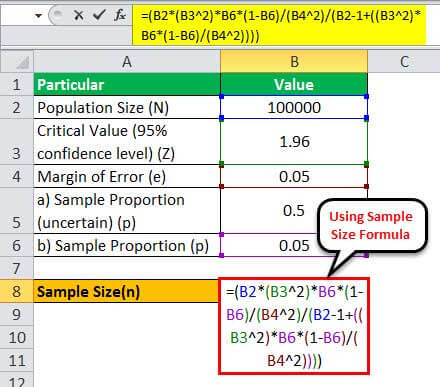
= (100000 * (1.96 ²)*0.05*(1-0.05)/(0.05 ²)/(100000 – 1+((1.96 ²)* 0.05*(1-0.05)/(0.05 ²))))

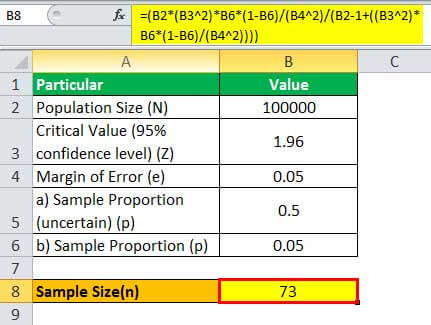
Therefore, the sample size for N = 120,000 can be calculated as,

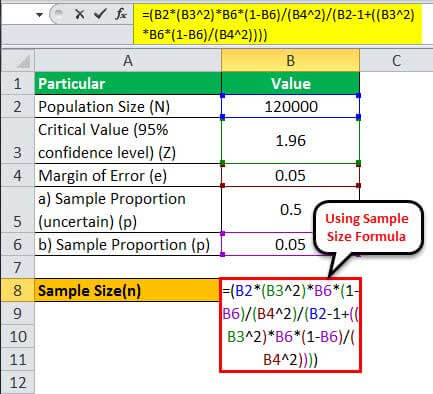
= (120000 * (1.96 ²)*0.05*(1-0.05)/(0.05 ²)/(120000 – 1+((1.96 ²)* 0.05*(1-0.05)/(0.05 ²))))

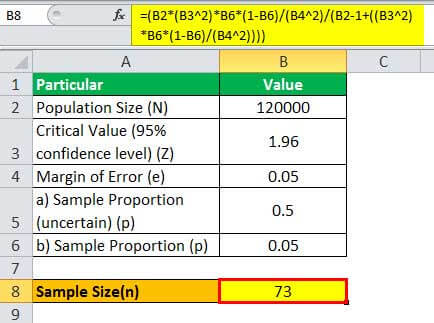
Therefore, it is proved that as the population size increases to be very large, it becomes irrelevant in the computation of the sample size.

Relevance and Uses

Sample size calculation is important to understand the concept of the appropriate sample size because it is used for the validity of research findings. In case it is too small, it will not yield valid results, while a sample is too large may be a waste of both money and time. Statistically, the significant sample size is predominantly used for market research surveys, healthcare surveys, and education surveys.

Sample Size Formula