Interest Rate Derivatives

Interest Rate Derivatives are the derivatives whose underlying is based on a single interest rate or a group of interest rates; for example, interest rate swap, interest rate vanilla swap, floating interest rate swap, and credit default swap.

You should know what derivative security is if you are reading this material. It is a security that derives its value from an underlying asset. The underlying asset could be anything ranging from a company's stock, a bond, metals, commodities, and other asset classes. If the underlying is an interest rate, the derivative security becomes an interest rate derivative. The underlying interest rates depend on the contract, which is agreed to by the counterparties and can range from LIBOR, domestic interbank offered rates, Fed Funds Rate, etc.

• Index options are regulated financial instruments and are traded on organized options exchanges. Regulatory bodies oversee these exchanges to ensure fair and transparent trading practices.
• Moreover, interest rate derivatives are of two types swaption and cap floors.
• Hence, A swaption is a financial derivative that gives the holder the option to enter into an interest rate swap. It's an option on an exchange. Swaptions are used for hedging and speculative purposes, and they play a significant role in managing interest rate risk in financial markets.
• A cap floor, or a cap and floor, combines two financial derivatives: an interest rate cap and an interest rate floor. These derivatives are used to manage interest rate risk and provide protection against interest rate fluctuations.

This is an important and exciting area under fixed income derivatives. It is an example of a structured transaction to hedge risks in a fixed income investment.

A swap is a contract between counterparties to exchange a series of intermediate cash flows arising throughout the tenor/life of the trade. Almost every swap contract comes under an interest rate swap. Most of them are variants of interest rate swaps.

Interest Rate Swaps

So what is an interest rate swap (IRS)?

An IRS is a swap contract to exchange a series of intermediate cash flows based on interest rates on a notional amount throughout the swap's tenor.

In general, they come in the form of exchanging cash flows from a fixed interest rate for cash flows from a floating interest rate over the swap's tenor. This type of trade is also known as a set for a floating swap where the leg of the swap pays/receives a fixed rate, and the other leg, a floating rate. It is also called a plain vanilla IRS.

Here’s a simple example to illustrate a fixed for the floating swap. We all know that a bank takes deposits and makes loans. Let’s assume that for the deposits Bank A takes, they pay a fixed interest rate of 5%. For the loans they make, let’s presume they charge a floating rate of interest, which is the LIBOR (say 3%) plus a spread (3%) over it to account for the borrower's riskiness. The spread is fixed, but the LIBOR keeps changing. If, for example, LIBOR falls to 1% or below by year-end, banks will be paying a constant 5% on deposits but charging lesser on their loans. To safeguard against this risk of making a lower interest margin ultimately due to rates falling, they enter into an IRS with another Bank B. Take some time to think about how the IRS would be structured.

Done? Here it is – Bank A currently pays fixed and receives floating on its deposits and loans, respectively. They will enter an IRS with Bank B to pay to float and receive fixed for a certain period, say three years. Effectively, the structure of the transaction will look like this:

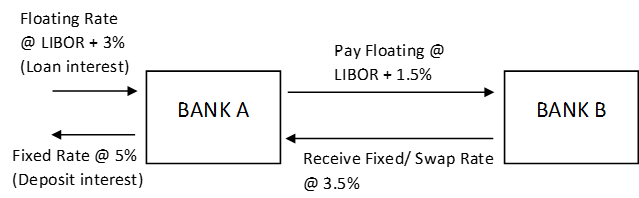
The Swap Rate here is only indicative – a no-arbitrage rate has been calculated.

As mentioned earlier, the swap payments/cash flows are based on a notional amount. Bank A's exposure to interest rates is benefited by paying floating on the swap. If rates go up above 5%, Bank A still benefits since it pays a lower rate on its deposits, and the higher rate will be passed on through the loans it makes, which finance the swap's floating leg. Why does Bank B act as a counterparty to Bank A? Simply because they would have the opposite exposure where they pay floating on their deposits and receive fixed on their loans.

I hope you got the structure of a swap. Counterparties agree to swap since they either have opposite views or exposures to the underlying.

Currency Swap

These are also called Cross Currency Swaps or Cross Currency Interest Rate Swaps. A good way to refer to it is “Xccy IRS.” As you would guess, this is a variant of an IRS, the difference being two different currencies involved.

A typical transaction would be Bank A (Japanese bank) borrowing say $10m (Notional amount) @ 5% p.a. and lending ¥100m (Notional amount) @ 3% p.a. to Bank B (US bank) for five years as part of an Xccy swap. Bank A pays B $500,000 to Bank B, while Bank B pays ¥3m to Bank A as swap payments every year throughout the life of the swap. This is a fixed-for-fixed swap, as you can notice.

A fixed for fixed Xccy IRS is simple. A fixed for floating Xccy IRS works similarly to an equivalent IRS except for two currency legs. A fixed floating IRS will have the intermediate cash flows netted against each other depending on a gain or loss. For example, Bank A may borrow $10m at LIBOR + 2% instead of 5%. If Bank A's interest payment at the end of the year is $300,000 and Bank B's is $500,000 after converting to USD, then Bank B will pay the difference of $200,000 to A. Similar would be the case when A has to pay B the difference.

A floating for floating Xccy IRS (Basis Swap) and normal IRS is also part of the structuring game. Though it is easy, we can end this discussion here rather than get deeper and deeper.

Difference between an Xccy swap and an IRS

An Xccy swap and an IRS differ apart from the currency legs. The Notional amounts on which the interest payments/cash flows are made are exchanged in the beginning and end in an Xccy swap. The same doesn’t hold for an IRS. In the earlier example, the notional principal of $10m and ¥100m are exchanged at the beginning and end. Therefore an Xccy swap eliminates currency risk or exchange rate risk of the notional principal amounts.

Other types of Swaps

There are other types of swap derived from interest rates like an Equity swap or a Total Return Swap (TRS), where the swap rate is paid on one leg, and the other leg pays equity/equity index-related payments like the dividends and capital gains differences; Overnight Indexed Swap (OIS) which is a fixed for a floating swap where the floating rate is based on a geometric average of floating rates on an overnight index say LIBOR or Fed Funds.

 Uses of Swaps

Just like any other derivative contract, swaps are used as a tool to hedge risk. The examples mentioned till now emphasized swaps as a tool to hedge risk. Meanwhile, they can also speculate on interest rates where a counterparty may not have an initial exposure. Thirdly, they can be used to make arbitrage gains if the swap rates are slightly mispriced. Here, the mispricing difference is quickly noticed whereby multiple entities would like to make a riskless profit, ultimately making this demand and supply lead to an equilibrium rate that cannot be arbitraged away.

Given that we’re on the topic of swaps, it would be right to introduce this type of interest rate derivative.

Swaption

This is an option on swap – a double derivative. It isn’t difficult, though. An option gives the buyer of the option the right but not the obligation to buy or sell the underlying at a predetermined strike price on a future date (at expiration in the case of European Options; before or at expiration in the case of American Options). You can google up for more options.

In the case of a Swaption, the strike price is replaced by a strike rate, an interest rate based on which the buyer can choose to exercise the option, and the underlying is a swap. More theory will only complicate things, so here’s a simple example.

ABC buys a 3-year Swaption where they pay fixed and receive floating (they buy a payer Swaption) at a strike rate of 2% exercisable at the end of one year. If the reference rate is greater than 2% at expiration, ABC will exercise the option following which the swap takes effect for three years. The option will not be exercised if the reference rate is less than 2%.

Caps and Floors

As the terms should indicate, a Cap caps one's risk, and Floor floors one's risk. Caps and Floors are options on interest rates, i.e., the underlying is an interest rate, and the strike rate is the rate at which the buyer exercises the option. They are generally issued with Floating Rate Bonds/Notes (FRNs).

Caps consist of a series of ‘Caplets’ and Floors of ‘Floorlets.’ Caplets and Floorlets are essentially caps and floors but with short time frames. A one-year Cap may consist of four Caplets with a tenor/expiration of 3 months each.

Generally, a Cap transaction goes like this: ABC Corporation issues a floating rate bond at LIBOR+2%, where LIBOR may be at 3%. The risk for ABC is if interest rates or LIBOR rise quickly, say in a year, they have to pay higher rates. So, along with the bond, they buy a Cap from a bank at a strike of 3.5% so that if LIBOR goes above 3.5%, ABC exercises the Cap. Exercising makes ABC pay only 3.5%, and they make the profit, which is the difference between LIBOR or the reference rate and 3.5% over that period.  The profit helps repay the increase in LIBOR; thus, ABC is effectively capped in his payments.

In the worst-case scenario, ABC ends up paying only 5.5%. If ‘minus (-)’ indicates outflows and ‘plus (+)’ inflows, here is how it would look for ABC Corp if the payments were agreed on an annual basis:

FRN payments:  ‒ (LIBOR + 2%)

Cap related payment: +LIBOR – 3.5%

Combining both would give:  – 3.5% – 2% = –5.5%, thus limiting the borrower’s exposure to interest rate changes.

A floor similarly would be combined with an FRN but by lenders. So ABC Corp's bond lender would buy a floor to limit their exposure to interest rate changes. This time, you should be able to structure the transaction without my giving you an example.

There are variants of caps and floors, one of them being ‘interest rate collars,’ which are a combination of buying a cap and selling a floor but let’s not get into that.

Learn more about Options and Trading Strategies

These are forward contracts on interest rates between counterparties. FRAs are contracted to borrow or lend money at a predetermined rate on a notional principal at a future time.

ABC may enter into an FRA to borrow @ 5% on a notional amount for three months, starting after six months (a 6X9 FRA – an FRA expiring after six months to borrow money for three months). This helps ABC in the event of 3-month interest rates going up at the end of 6 months from today.

ABC could also enter into an FRA to lend @ 5% on a notional amount for three months, starting after six months (a 6X9 FRA – an FRA expiring after six months to borrow money for three months). This helps ABC in the event of 3-month interest rates going down at the end of 6 months from today.

The examples given might be overly simplistic, practically Interest Rate Derivatives. The concepts are quite simple, but we have not gone into the nitty-gritty of the workings. The calculations are a bit complex, but it is fair if we understand the concepts for now. Sometimes being the jack of all might be worth it – the world lacks good generalists. Go over the concepts explained, try getting the hang of it, and answer the open-ended questions under each concept because it ultimately helps strengthen your understanding and makes you think. As regards practical examples, there are loads of examples on swaps, lesser-known ones on interest rate options, and FRAs, although they are done very regularly. Google those once you get the hang of these concepts to understand them better.

• Top Derivatives Careers
• Derivatives in Finance
• What is C Corporation?
• Bond Pricing