One-Tailed Test

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

One-Tailed Test Definition

The one-tailed test is a statistical hypothesis testing method. To reject the null hypothesis sample mean should be either greater or less than the population mean. This test is also referred to as a directional test or directional hypothesis. The test is run to prove a claim either true or false.

The determination of this test cannot be ambiguous, meaning that it can be either less or more than the population mean but cannot be both. Hypothesis testing determines the probability of a hypothesis being correct. The test validates the accuracy of the alternate hypothesis by eliminating randomness.

One-Tailed Test Definition

For a one tailed test hypothesis, the sample mean value can be either more or less than the population mean value but cannot be both.
The null hypothesis and alternative hypothesis precede one-tailed tests—along with a p-value (probability value).
The test is directional; hence it does not consider the other direction while establishing a relationship.

One Tailed Test Explained

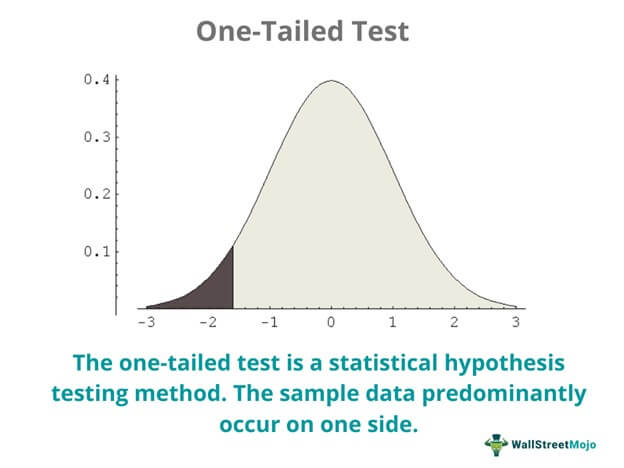
The one tailed test is a statistical method of hypothesis testing. Based on statistical data, hypothesis testing determines whether a theory is true or not. If a test shows the mean sample being both larger and smaller than the population, it is a two-tailed test. But when a test shows the sample mean being only larger or smaller than the population, it is a one tailed test. So, during testing, if sample data predominantly occur on one side, then the null hypothesis will be rejected—an alternate hypothesis would be accepted.

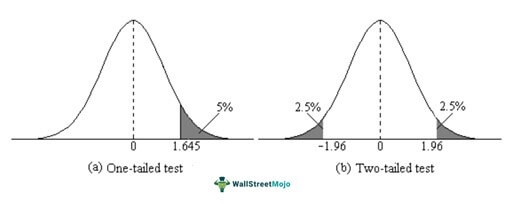
One-tailed tests are preceded by the null hypothesis and alternative hypothesis. Researchers are required to prove the null hypothesis wrong; only then can they claim the alternative hypothesis. Ideally, in order to prove a theory, researchers need to eliminate randomness. When they prove an observation caused by a specific cause, the observations should not be caused by random factors. Randomness levels are determined by statistical significance.

A significance level is represented as "p," referring to probability. Usually, significance values are either 1%, 5%, or 10%. However, researchers have the discretion to use any other probability. The probability value is calculated assuming that the null hypothesis is true. The lower the p-value, the lesser the randomness—the null hypothesis will easily be proven false. If the resulting p-value is below 5%, the difference between both observations is statistically significant, and the null hypothesis is rejected.

Example

Let us understand the application of one-tailed tests with an example.

Let us assume a school principal wants to prove that a new math professor increased classroom performance by 9.29%. The principal set up the null (H0) and alternative (Ha) hypotheses:

H0: μ ≤ 9.29

Ha: μ > 9.29

The principal hopes to reject the null hypothesis and validate his claim as the alternative hypothesis. If the test rejects the null hypothesis, the alternative hypothesis is supported. On the contrary, if the test outcome fails to reject the null hypothesis, the principal will have to research further to discover other explanations for the classroom performance.

The rejection region lies on one side of the sampling distribution. Therefore, to determine how the classroom performed compared to a different mathematics professor, the principal must run a right-tailed significance test—extreme values must fall on the right side of the normal distribution curve. A normal distribution or Gaussian distribution refers to a probability distribution where the values of a random variable are distributed symmetrically. These values are equally distributed on the left and the right side of the central tendency. Thus, a bell-shaped curve is formed.

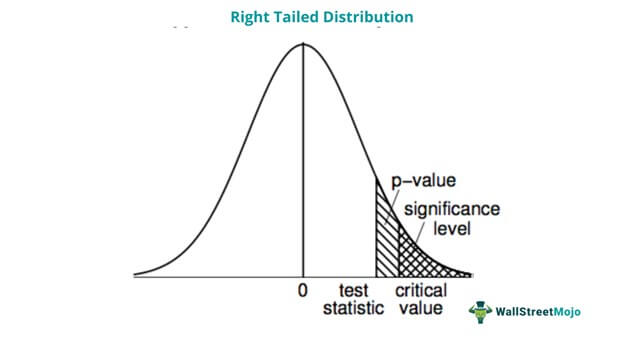
The one tail test results, represented in the right-tail curve area could show an overlap between increased classroom performance and the period taught by the new professor. Further, the test will show if the results were significantly different for the previous professor.

One-Tailed Test vs. Two-Tailed Test

One Tailed Test	Two Tailed Test
In one tailed tests, alternative hypotheses have only one end.	In a two-tailed test, the alternative hypothesis has two ends
It is a directional hypothesis	It is a non-directional hypothesis
The region of rejection can be either left or right.	Region of rejection can be both left as well as right.
There is a relationship between variables in a single direction.	There is a relationship between variables in either direction.
The result is always greater or less than a specific value.	The result is greater or less than a certain value range.
Denoted by > or <	Denoted as ≠

Frequently Asked Questions (FAQs)

When to use one tailed tests?

One tailed tests are used in situations where a theory or statement is set to be either true or false. Assume that a new drug is developed. The developers want to check if it is more effective than the current drug. In such scenarios, one tailed test can be used to prove the effectiveness.

On what hypothesis the one-tailed test is based?

It is based on two hypotheses—the null hypothesis and the alternative hypothesis. The test will prove only one of them true. Researchers want to prove the null hypothesis false to establish their findings as the alternative explanation for the sampled data.

What are the advantages of using one-tailed vs. two-tailed tests?

One tail tests have a very practical advantage—it demands fewer subjects to obtain significance. On the other hand, a two-tailed test splits the significance level and then implies it in both directions. Thus, each direction is half as strong as a one tail test.