Uniform Distribution

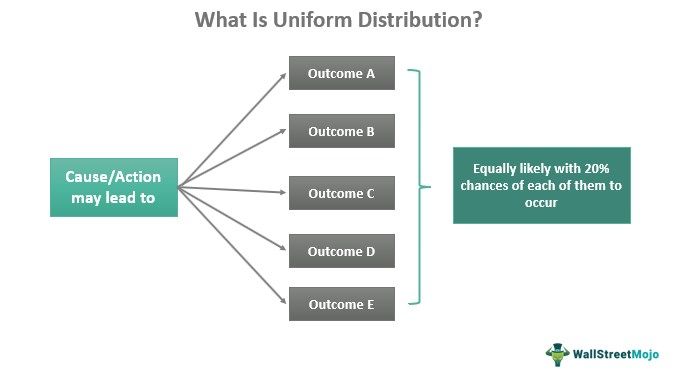
Uniform distribution is the statistical distribution where every outcome has equal chances of occurring. Researchers or business analysts use this technique to check the equal probability of different outcomes occurring over a period during an event. This, in turn, helps them prepare for all situations having equal chances of occurrences.

Indicating the equally likely probability, they are represented with a horizontal line parallel to the X-axis, featuring the cause, event, or action. It differs from a normal distribution, signifying the data around/close to the mean occurring frequently.

• Uniform distribution refers to the type of distribution that depicts uniformity. It means every possible outcome for a cause, action, or event has equal chances of occurrence.
• Discrete and continuous are two forms of such distribution observed based on the type of outcome expected.
• Like normal distribution, its uniform counterpart is also symmetric in nature, i.e., both the sides of the graph are mirror images of each other.
• When users plot the chances of each outcome to occur on a graph, a line parallel to the X-axis is derived.

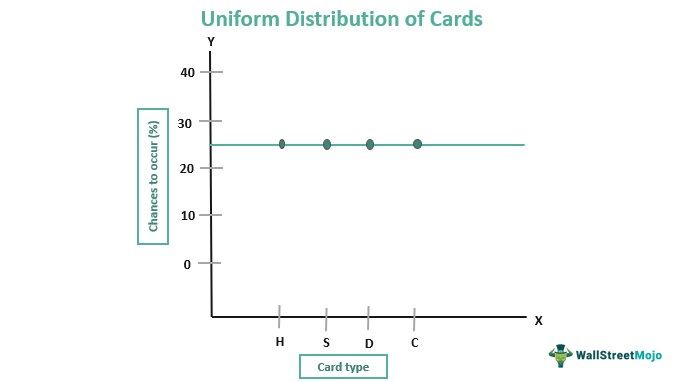
Uniform distribution probability symbolizes uniformity in the chances of different outcomes occurring due to a cause, action, or event. When users plot the chances of each outcome to occur on a graph, they get a line parallel to the X-axis, indicating the chances of the values of variables on the X-axis to occur.

For example, if one desires to find out the probability of one card from Heart, Spade, Diamond, and Club to be selected from the deck of cards, each of them is equally likely to be chosen whenever a player takes out a card. Thus, each card from the deck has a 25% chance of selection every time a user takes them out. The same is the case with the dice, where every number has equal chances of appearing whenever players roll and throw it.

Uniform distribution is of two forms – discrete and continuous. This bifurcation depends on the type of outcomes with possibilities of occurrence.

A discrete uniform distribution is the probability distribution where the researchers have a predefined number of equally likely outcomes. For example, when rolling dice, players are aware that whatever the outcome would be, it would range from 1-6. Here, users identify the expected outcomes beforehand, and they understand that every outcome will have a 1/6 chance of occurring.

Another one is the continuous distribution, which does not define the expected occurrences. Also referred to as a rectangular distribution, given the rectangular shape formed once the values are plotted on a graph, these ensure the equal chances of occurrence of each outcome but do not specify the number of probable effects/outcomes, signifying infinite existence.

It is a symmetric probability distribution. Thus, any event or experiment here may have an arbitrary outcome for chosen parameters or bounds. The parameters a and b are the minimum and maximum bounds. There are intervals, either an open interval or closed interval, calculated as the difference between maximum and minimum bounds. Determination of probabilities in this form of distribution is easy to assess. Hence, it forms the basis for hypothesis testing and cases of sampling in addition to its use in finance.

Researchers or analysts, however, need to follow the below-mentioned steps to calculate the expected value of uniform distribution:

1. Asses the maximum and minimum values
2. Find out the interval length by subtracting the minimum value from the maximum value.
3. The next step is to find out the probability density function. Here, the user can divide the unity by the interval length.
4. Now, find out the mean of the values.
5. Calculate the uniform distribution variance.
6. Compute standard deviation by finding the square root of the variance.

The value of the expected outcomes is normally equal to the mean value for a and b, which are the minimum and maximum value parameters, respectively. The mean will be :

Mean of the Uniform Distribution= (a+b) / 2

The variance of the uniform distribution is:

σ² = b-a² / 12

The density function, here, is:

F(x) = 1 / (b-a)

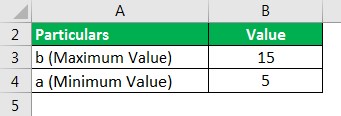
Suppose an individual spends between 5 minutes to 15 minutes eating his lunch. For the situation, let us determine the mean and standard deviation.

Here is the data available for the calculation.

Mean of the Distribution

• = (15+5)/2

Mean will be –

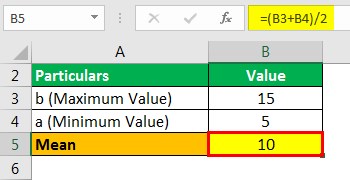
• Mean = 10 minutes

Next, the calculation of standard deviation of the uniform distribution will be –

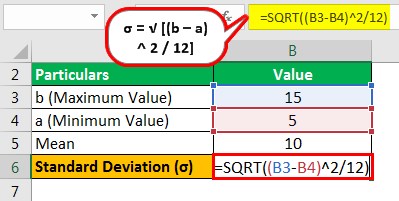
σ = √ = √

= √

= √ 8.33

Standard Deviation will be –

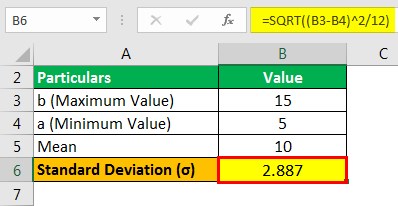
• σ = 2.887

Therefore, the distribution shows a mean of 10 minutes with a standard deviation of 2.887 minutes.

Both uniform and normal distributions are symmetrical, displaying a line down the center of the distribution when plotted on the graph. This means one side of the distribution will perfectly be a mirror image of another. 

Though there are similarities, they differ majorly in their shape. While normal distribution has a bell shape, its uniform counterpart is rectangular, indicating an equally likely probability of different outcomes to occur.

This is a guide to what is Uniform Distribution & its definition. Here, we explain the probability distribution, its variance, formula, and example. You can learn more from the following articles - 

• Exponential Distribution
• Kurtosis
• Empirical Rule