Balloon Mortgage Calculator

The Balloon Mortgage calculator is used to calculate the amount of balloon balance due at the end of the term of the loan. The formula to calculate a balloon balance is similar to that used to calculate the outstanding balance on a mortgage loan.

Balloon Mortgage Calculator

PV x (1+r)ⁿ – P x [(1+r)ⁿ – 1 / r]

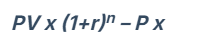
Wherein,

PV is the present value of Original Balance
P is the Payment
r is the rate of interest
n is the frequency of payments

ROI (r)

Balloon Mortgage Calculator

How to Calculate?

One needs to follow the below steps in order to calculate the monthly installment amounts.

First, we will calculate the equal periodical installments assuming no balloon repayment, and we shall begin with the principal amount.
Multiply the principal amount or the loan amount by a rate of interest.
We need to compound the same by rate until the loan period.
We now need to discount the above result obtained in step 3 by the following:
After entering the above formula in excel, we shall obtain periodically installments, which are mostly monthly repayments.

Now, there would be a term wherein the loan must be paid in full. Take the Loan amount as PrincipalLoan Amount As Principal Loan Principal Amount refers to the amount which is actually given as the loan from the lender of the money to its borrower and it is the amount on which the interest is charged by the lender of the money from the borrower for the use of its money.read more Value, the installment amount as the payment, and the rate of interest, and insert the same in the above mentioned equation.

The resultant figure would be the balloon paymentBalloon Payment The balloon payment is a huge sum paid at the end of a loan tenure. Most balloon loans come with a short-term tenure; it could be a commercial loan, mortgage, or fully amortized loan. Also, the final installment is at least double the previous installments.read more required to be made.

Balloon Mortgage Examples

You can download this Balloon Mortgage Calculator Excel Template here – Balloon Mortgage Calculator Excel Template

Below are a few examples of the Balloon Mortgage Calculator.

Example #1

Mr. Zee has taken a Balloon Mortgage loan, which states its term as 10/15, with an annual rate of 7.5% compounded monthly. The loan amount that was borrowed was $132,000. The monthly installment amount that Mr. Zee is supposed to pay comes to around $1,223.66

Based on the above information, you must calculate the Balloon mortgage amount required to be paid at the end of the term.

Solution:

The term structureTerm Structure The term structure is the graphical representation that depicts the relationship between interest rates and various maturities. The graph itself is called a “yield curve.” The term structure of interest rates plays an essential part in any economy by predicting the future trajectory of rates.read more is that the loan will be amortized for 15 years, and we need to find out what amount it shall pay at the end of 10 years as a lump sum payment.
We can use the below formula to calculate the future value of the balloon payment to be made at the end of 10 years: FV = PV*(1+r)ⁿ–P*[(1+r)ⁿ–1/r]
The rate of interest per annum is 7.5%, and monthly it shall be 7.5%/12, which is 0.50%.

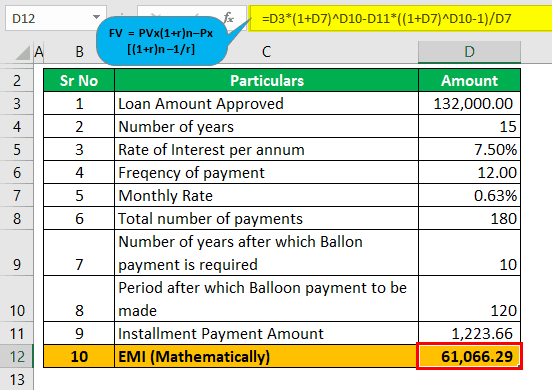
= 100,000*(1+0.50%)¹²⁰–1,223.66 x [(1+0.50%)¹²⁰–1/0.50%]

= 61,066.29

The remaining balance that shall be paid with the final payment will be $61,066.29, which is the balloon payment and has to be paid at the end of 10 years.

Example #2

Company X wanted to buy new properties in a posh area in their city. But due to the recent hike in property prices, they are unwilling to invest a large amount. Hence, they opt for hiring the properties at leaseLease Leasing is an arrangement in which the asset's right is transferred to another person without transferring the ownership. In simple terms, it means giving the asset on hire or rent. The person who gives the asset is “Lessor,” the person who takes the asset on rent is “Lessee.”read more. They knew that if they hired property on lease, the cash outflow would be too high for them. The market rate of interest at which they can borrow is 8%.

Further, they are anticipating higher cash flowers shortly, say in the next five years, and they would be able to purchase the property. Henceforth, they decide to take it on lease and purchase it after five years. The term structure of the loan is 5/12, and the property’s value is $270,000. Since the background of the company and directors is too good, they have been offered 100% financing. The monthly installment amount shall be 2,922.62 You must calculate the balloon payment that the company shall be required to make at the end of 5 years, whereas a loan is amortizedLoan Is Amortized Loan amortization schedule refers to the schedule of repayment of the loan. Every installment comprises of principal amount and interest component till the end of the loan term or up to which full amount of loan is paid off.read more for 12 years.

Solution:

The term structure is the loan will be amortizedLoan Will Be Amortized The amortized loan formula is used to calculate the annual or monthly payments a borrower must make to the lender for the loan they have taken out. Annual interest payments plus the annual portion of the long-term debt make up the yearly payment.read more for 12 years, and we need to find out what amount it shall pay at the end of 5 years as a lumpsum payment.
We can use the below formula to calculate the future valueFormula To Calculate The Future Value The Future Value (FV) formula is a financial terminology used to calculate cash flow value at a futuristic date compared to the original receipt. The objective of the FV equation is to determine the future value of a prospective investment and whether the returns yield sufficient returns to factor in the time value of money.read more of the balloon payment to be made at the end of 5 years: FV = PV x (1+r)ⁿ – P x [ (1+r)ⁿ – 1 / r ]
The rate of interest per annum is 8.00%, and monthly it shall be 8.00%/12, which is 0.67%.

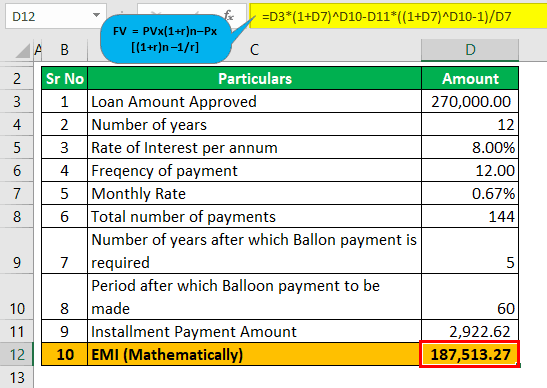
= 270,000 x (1+0.67%)⁶⁰ – 2,922.62 x [ (1+0.67%)⁶⁰ – 1 / 0.67% ]

= 187,513.27

The remaining balance that shall be paid with the final payment will be $187,513.27, which is the balloon payment and has to be paid at the end of 5 years.

Conclusion

A balloon Mortgage calculator is generally seen in the mortgage market, and the benefit they have is that initially, they require lower payments. Balloon Mortgages can be preferable for those people or firms who have cash flow issues in the near term, and further, they expect higher cash flows later somewhere in the future when the balloon payment is near. The borrower must be prepared at the end of the loan term to make their balloon payment.

Balloon Mortgage Calculator