Bayes Theorem

What Is Bayes Theorem?

The Bayes theorem is a mathematical calculation of the conditional probability of an event A occurring after event B. Here, event B, having taken place already, is the condition. Thus, the Bayes theorem predicts the occurrence of an event when another similar event has already taken place. Also, the occurrence of these two events is independent of each other.

Bayes theorem is also called Bayesian inference. This conditional probability measure is applied widely in statistics, finance, machine learning, philosophy, sports, medicines, law, and engineering. It is also used for deriving reverse probabilities—when the conditional probability of an event is already known.

• Bayes theorem is statistical inference. It is used to find the conditional probability of an event occurring when a similar event has already occurred.
• Thomas Bayes gave the Bayes law in the 18th century. Bayes was a British clergyman, statistician, and philosopher,
• To determine the conditional probability of event A occurring after the completion of event B, the following formula is used:
  P (A│B) = / P(B).

Bayes Theorem Of Probability Explained

The Bayes theorem definition (Bayes rule) is a probability measure proposed by British statistician Thomas Bayes. His findings were compiled in an essay, "Towards Solving a Problem in the Doctrine of Chances." In 1763, the essay was posthumously published by the Philosophical Transactions of the Royal Society. Soon mathematicians, economists, researchers, and financial analysts adopted it as a statistical probability technique.

Its application is not just limited to just finance and investment sectors. This tool is crucial for machine learning and artificial intelligence as well. Specifically, it is used for predictive modeling—correlating available data with a model for gauging the posterior distribution—when likelihood and prior distribution are known.

The different terms associated with the Bayes theorem are as follows:

• Conditional Probability - When the happening of an event A depends on the occurrence of another event B, it is known as conditional probability.
• Posterior Probability - The conditional probability of an event happening based on new information or prior probability is known as posterior probability.
• Prior Probability - It is the probability of an event's occurrence based on previous information.
• Joint Probability - The chances of two or more events taking place simultaneously is their joint probability.
• Random Variables - The continuous range of values denoting the outcome of random experiments are the random variables.

Formula

The Bayes theorem determines the probability of an event A occurring based on the probability of the occurrence of event B—provided both events occur independently. The following Bayes theorem formula represents it:

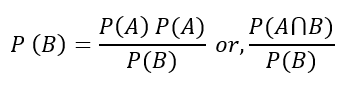
• P(A|B) is the probability of event A occurring after event B.
• P(B|A) is the probability of event B occurring after event A.
• P(A) is the probability of event A occurring.
• P(B) is the probability of event B occurring.

Calculation Example

Let us look at how the Bayes theorem probability calculator works. Assume that there are two investment options, A and B. Then, the probability of generating positive returns from A is 74%, and the probability of generating positive returns from B is 45%. Also, the possibility of investment B providing a positive return when investment A also provides a positive return is 13%.

Based on the given data, determine the probability of investment A providing a positive return when investment B also provides a positive return.

Solution:

Given:

P (A) = 0.74

P (B) = 0.45

P (B│A) = 0.13

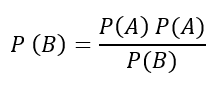
P (A│B) = = 0.21

Thus, the probability of generating positive returns from investment A when investment B also generates positive returns is 0.21.

Applications Of Bayes Theorem

The Bayes law is the base of Bayesian statistics. It is applied to various fields to determine the probability of an event using past experiences and evidence. Such analyses can help predict unfavorable outcomes. Also, once an unfavorable outcome is predicted, an organization can prepare itself with corrective measures.

Thus, it is used in statistics, medicine, machine learning, engineering, philosophy, sports, finance, humanities, and law. Now, let us go through some real-life Bayes theorem examples to understand the application of the Bayes rule:

• In finance, Bayes law determines the risks and returns of an investment.
• It is also used for determining credit ratings. Lenders analyze the uncertainty associated with debt recovery. Every potential lender is screened before sanctioning funds.
• In medical science, this tool is used for determining the accuracy of results (results of a medical test).
• In machine learning and artificial intelligence, Bayesian statistics help detect spam and credit card fraud.
• Many sports betting (prediction) algorithms are based on the results of the Bayes theorem.
• In a court of law, this rule is applied to check the validity of evidence. Alternatively, the tool is used to prove a lack of evidence.
• Bayes law is used for forecasting weather—rain, thunderstorm, etc.

Frequently Asked Questions (FAQs)

Recommended Articles

This article is a guide to What is Bayes Theorem. Here, we explain its definition, formula, applications, and calculation with examples. You can learn more about it from the following articles -

• Posterior Probability
• Empirical Probability
• Independent Variable