Bayesian Modeling

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

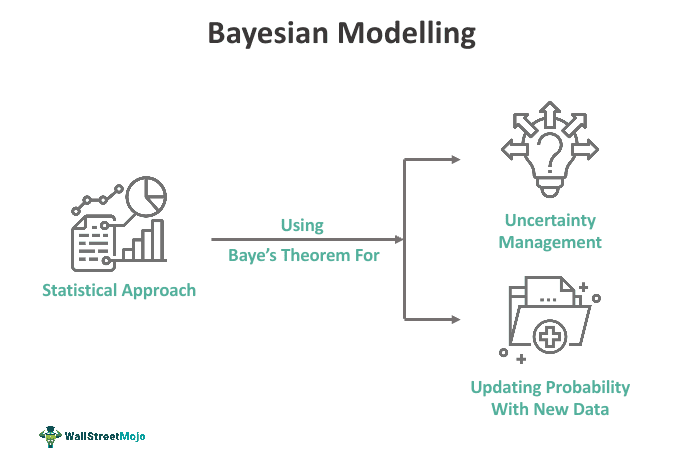
Bayesian modeling is a statistical framework that uses probability theory to model uncertainty and makes inferences about parameters and predictions. It aims to draw inferences about unknown parameters or quantities based on observed data, forecasts future results, and guides decision-making under uncertainty.

It helps in appraising one's belief with the availability of new data. Hence, it aids in clustering, regression, and classification in machine learning. In finance, it helps in risk assessment, making investment decisions, and setting the price of financial products. In medicine, it calculates posterior probability to check the safety and effectiveness of a drug using clinical data.

What Is Bayesian Modeling?

Bayesian modeling is a statistical method that employs Bayes' theorem to handle uncertainty by updating probabilities with new data.
It makes inferences about unknown parameters or quantities based on observed data, predicts future outcomes, and assists in decision-making in uncertain situations.
Moreover, Bayesian model averaging combines various models for more accurate predictions by assigning weights based on their efficiency, reducing errors, accounting for uncertainty, and improving multiple fields like science, finance, and machine learning.
Hence, various industries widely use it, including medical diagnosis, marketing campaign optimization, cosmological model analysis, educational data analysis, financial prediction, document classification, and information retrieval.

Bayesian Modeling Explained

Bayesian modeling is rooted in Baye's theorem, utilizing statistical methods to update knowledge concerning model parameters with observed data. Professionals like doctors, engineers, and finance have used it as the most powerful tool in making decisions under uncertain shreds of evidence. Moreover, Bayes theorem, which is a mathematical formula, forms its basis. It tells us how individuals can update their beliefs about the world under new pieces of evidence.

Reverend Thomas Baye proposed a formula to update probabilities using new evidence in the eighteenth century. With the progress of time and the advent of supercomputers plus new algorithms, it became widely used in finance. Furthermore, it works by amalgamating two pieces of information, like prior knowledge and observation data. Prior knowledge means the prevailing knowledge regarding the world, like the probability of other events or model parameters.

Observational data is the collected data from, say, survey results or financial markets. After that, the modeling mixes these two information to get posterior distribution.
Hence, individuals simply update their beliefs under the new dataset. It has various significant implications in the finance world. Its posterior model helps make wise investment decisions and guides on managing risk and allocating funds.

Bayesian models incorporate prior knowledge to enhance predictions in the relationship between different asset prices. Therefore, it gives more accurate forecasting of stock prices.

Additionally, it facilitates portfolio development and risk mitigation. The Bayesian modeling framework provides a coherent and flexible approach to statistical modeling and inference. Also, hierarchical Bayesian modeling and Bayesian modeling in R and Python are essential techniques in probability and Bayesian modeling. Furthermore, these methods use Bayes' theorem to update probabilities based on prior beliefs and new data, allowing for more accurate decision-making and inference.

Bayesian Model Averaging

It is a statistics technique combining forecasts of numerous models, producing highly accurate predictions. Hence, it theorizes that no single model is perfect, so only their combination can decrease the error holistically. Moreover, this attaches a definite weight to every model, representing the probability of the model being correct. Furthermore, it assigns the models' weights per their efficiency inside the training data set.

After that, the models are missed together for the last prediction. It scores over other techniques as it can account for model uncertainty. Additionally, it has less probability to overfit the training data. Thus, it leads to more correct predictions than others.

Overall, this model augments science in design experiments, data analysis, and inference about earthly life. It can also facilitate in creation of new statistical methods for improving the accuracy of prevalent methods. Likewise, it is applied in finance for better investment decisions and accuracy improvement in machine learning.

Examples

Let us take the help of a few examples to understand the topic.

Example #1

Suppose an investor named Alex wants to estimate the future price of a particular stock based on historical data. Rather than relying solely on traditional statistical methods, the investor chooses Bayesian modeling to incorporate both prior beliefs and observed data.

Thus, he begins with prior beliefs about the stock's potential price movements. These beliefs could be informed by industry trends, news, or the investor's historical experience. He updates their prior beliefs using Bayesian modeling as new daily stock price data becomes available. In this case, the likelihood function describes the probability of observing the current stock prices given different parameters. Through Bayes' theorem, he combines the prior beliefs with the likelihood function to obtain a posterior distribution, refining their understanding of the stock's potential future prices.

Moreover, the iterative process of this model allows Alex to refine their predictions as more data becomes available continuously. Whether it's adjusting to economic indicators or reacting to company news, the Bayesian modeling framework enables a dynamic and adaptive approach to stock price forecasting.

Example #2

In order to describe tracer evolution in ocean sediment transport and tracer concentrations, a new Bayesian approach is employed for parameter estimate and uncertainty quantification.

Hence, in a recent work, Edge et al. infer posterior distributions of important unobserved (latent) model parameters with uncertainty quantification using Bayesian inference techniques, notably Markov Chain Monte Carlo (MCMC) sampling. Even though MCMC methods are common, the concept is novel in how it applies to actual examples of sediment movement on the continental shelf, involving complex bottom boundary forcing and reaction. The method's implementation required the use of a 1-D advection-diffusion sediment transport model, which was made more difficult by the addition of unstable forcing. Additionally, three case studies with increasing complexity were taken into account.

Therefore, one of the motivating motivations behind the effort was the difficulty of obtaining direct in-situ measurements of the requisite latent features under deep ocean circumstances. They demonstrate how measurements of straightforward indicator parameters, such as current velocities and suspended sediment concentrations from acoustic backscatter, can provide information on difficult-to-observe properties. Their method represents a significant improvement in the use of Bayesian methods for estimating parameters in complicated numerical models, and it is readily generalizable to models of greater complexity.

Applications

Numerous industries use the Bayesian model extensively, including statistics, economics, medical research, etc. Hence, let us know its applications:

Medical diagnosis: Its networks have forayed into medical diagnosis, which helps evaluate the probability of illnesses per medical history and patient symptoms.
Marketing Campaign Optimization: It helps in customer behavior analysis to optimize marketing campaigns. Hence, it can successfully predict suitable marketing strategies.
Cosmological Model Analysis: All uncertainty concerning cosmology is considered during restricting parameters in cosmic models.
Educational Data Analysis: Inference about student performance and data analysis of educational research can be made using it.
Predictive Analysis in Finance: Statistical data and predictive analysis allow the financial field to evaluate probabilities in investment decisions.
Document Classification: It also aids document classification into different types, like spam detection.
Information Retrieval: For relevance ranking, Bayesian models are used by information retrieval systems.
Risk Assessment in Malaria: Malarial risk in patients is modeled utilizing the Bayesian technique.
Medicine: Here, it gets used in drug efficacy tests, medical diagnoses, and treatment planning.
Gene Regulatory Network: It is used to model gene regulatory networks and interactions.

Frequently Asked Questions (FAQs)

1. Bayesian modeling is based on the idea of?

Bayesian modeling's core is adapting our perspective with new data. The Bayes theorem, a math tool, guides us in adjusting our probability estimates for a hypothesis when new information emerges.

2. What is the Bayesian model in machine learning?

Machine learning often employs Bayesian models to create predictive models for fresh data.

3. What is the difference between the Bayesian model and linear regression?

The main difference between Bayesian models and linear regression lies in handling uncertainty. Bayesian models treat model parameters as random variables with probability distributions, allowing them to consider data uncertainty and provide more dependable predictions than linear regression.

4. What is Markov Chain Monte Carlo (MCMC) in Bayesian Modeling?

MCMC is a computational method used in this model to obtain samples from the posterior distribution without needing an explicit expression for it. It involves constructing a Markov chain that converges to the desired posterior distribution.