Maturity Value

Last Updated :

-

Blog Author :

WallStreetMojo Team

Edited by :

Ashish Kumar Srivastav

Reviewed by :

Dheeraj Vaidya, CFA, FRM

Table Of Contents

arrow

Maturity Value Definition

Maturity value is the amount to be received on the due date or on the maturity of instrument/security that investor is holding over its period of time and it is calculated by multiplying the principal amount to the compounding interest which is further calculated by one plus rate of interest to the power which is time period.

Table of contents

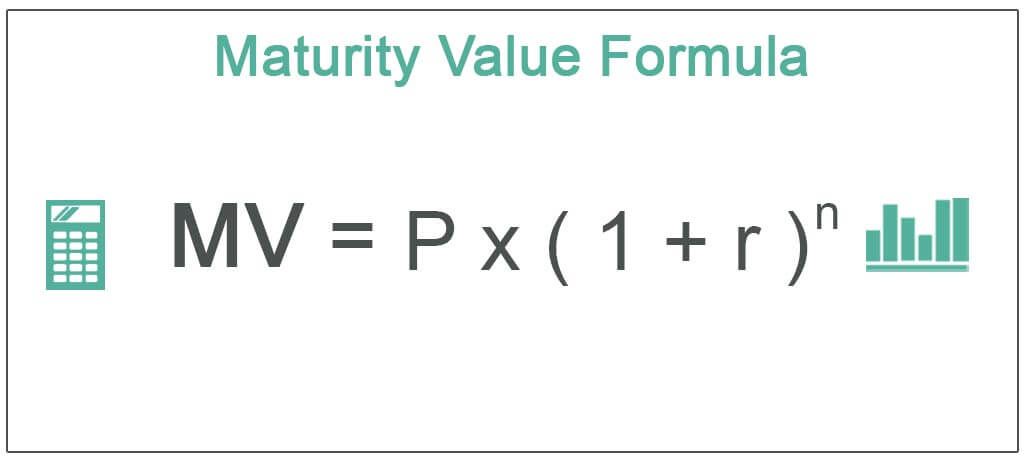
Maturity Value Formula

The formula for calculation of maturity value is as per below:

MV = P * ( 1 + r )n
Maturity-Value-Formula

Where,

  • MV is the Maturity Value
  • P is the principal amount
  • r is the rate of interest applicable
  • n is the number of compounding intervals since the time of the date of deposit till maturity

Explanation

The formula that is used for calculation of Maturity value involves the use of principal amount that is the amount which is invested at the initial period, and n is the number of periods for which the investor is investing in, and r is the rate of interest that is earned on that investment.

When one takes the frequency of compounding as a power to rate, it gets multiples, which is nothing but compounding, and then when that result is multiplied by principal amount, one gets the maturity value that one can have.

Maturity Value Formula Examples (with Excel Template)

Let's see some simple to advanced examples of Maturity Value Formula to understand it better.

Example #1

Mr. A invested 100,000 in bank fixed deposit at ABC bank ltd. ABC bank ltd. Pays 8.75% compounded annually. Calculate the maturity amount that Mr. A will get provided he invests for three years.

Solution:

Mr. A has invested in fixed deposits for three years, and since it's compounded annually, n will be 3, P is 100,000, and r is 8.75%.

maturity value formula example 1.1

So, the calculation of Maturity Value is as follows,

maturity value formula example 1.2
  • MV = 100,000 * ( 1 + 8.75% )3
  • MV = 100,000 * (1.286138672)

Maturity Value will be -

maturity value formula example 1.3
  • MV = 128,613.87

Example #2

John Bradshaw a high net worth individuals and has invested 60% of his investments in equities and now he is of the view that the market will go down in coming future and hence he wants to temporarily invest funds in debt to avoid risk and hence he is considering investing in CD which is an abbreviation for Certificate of Deposit.

Vista limited has issued CD, which states it will pay 9% interest that will be compounded monthly. Now suppose that Mr. John has invested 30% of his investments, which is $150,000 for 2 years. Calculate the maturity amount that Mr. John will receive at the end of 2 years.

Solution:

Mr. John has invested in Certificate of Deposit for 2 years, and since it is compounded monthly, n will be 2 x 12, which is 24, P is $150,000, and r is 9.00%, which p.a. and hence monthly rate will be 9/12 which is 0.75%.

maturity value formula example 2.1

So, the calculation of Maturity Value is as follows,

maturity value formula example 2.2
  • MV = $150,000 * ( 1 + 0.75%)24
  • = $150,000 * (1.196413529)

Maturity Value will be -

maturity value formula example 2.3
  • MV = $179,462.03

Hence, Mr. John will receive $179,462.03 at end of 2 years.

Maturity Value Formula - Example #3

Carol is a 45 years old woman working as a manager in an MNC located in New York. She is considering a retirement plan which was proposed to her by an investment advisor who advises her to invest a lump sum amount of $1,000,000 in his guaranteed retirement plan until she retires at the age of 60. He advises she would receive a lump sum amount of $3,744,787.29, and that plan appears to her to be lucrative. However, the investment advisor told her that it compounds quarterly, and the rate of return she would earn will be 12%.

However, she is not convinced with the rate of return that he says she would earn. You are required to calculate the rate of return that she will earn on this investment using the maturity value formula and advise whether the investment advisor has made a correct statement or he has bluff about the return?

Solution:

Carol will invest in the guaranteed retirement plan for 15 years, which is the time left until she retires at the age of 60, and since it's compounded quarterly, n will be 15*4, which is 60, P is $1,000,000, and r we need to find out, and here we are given the maturity value as $3,744,787.29

rate of interest example 3.1

We can use the below formula of maturity value and plug in the figures and arrive at the interest rate.

rate of interest example 3.2

MV = P * ( 1 + r )n

  • 3,744,787.29 = 1,000,000 x ( 1 + r )(60)
  • 3.74478729 = (1 + r)60
  • r = (3.7447829 - 1)1/60

So, Quarterly Rate of Interest will be -

rate of interest example 3.3
  • r = 2.23% quarterly

The yearly rate of interest will be -

rate of interest example 3.4
  • r (yearly)= 2.23 x 4
  • = 8.90% p.a.

Hence, the statement made by an investment advisor that she will earn 12% is incorrect.

Maturity Value Calculator

You can use the following Maturity Value Calculator.

Relevance and Uses

It's important for them to be able to calculate the maturity value of a note so that they can know how much a firm or the company or the business will have to pay when the note shall come due. Investment advisors use this formula to advise clients on the spot of the scheme they are selling and like how much amount they will have in hand.

A salaried person uses to calculate the fixed deposit they make with the banks in which they have their salaried accounts. The formula can be used to calculate the reverse interest rate when one has maturity value to know the true rate of interest earned on the investment, as we did in our last example.