Compounding Quarterly Formula
Last Updated :
-
Blog Author :
Edited by :
Reviewed by :
Table Of Contents
What Is Compounding Quarterly Formula?
Compounding quarterly can be considered as the interest amount earned quarterly on an account or an investment where the interest earned will also be reinvested. And is useful in calculating the fixed deposit income as most banks offer interest income on the deposits, which compound quarterly.
Further, it can be used to calculate any income on other financial products or money market instruments offering quarterly income. Thus it is the frequency at which the interest on an investment is added back or reinvested every three months, which is equal to four times in a year. With each addition of new interest, the subsequent calculation will include the new interest.
Table of contents
- Compounding quarterly refers to the practice of earning interest on an account or investment every quarter, with the earned interest being reinvested. This approach is particularly significant when calculating fixed deposit earnings, as many banks use quarterly compounding for interest payments on deposits.
- This approach can also be relevant when assessing the returns on various financial products or money market instruments that offer quarterly compounding.
- The power of compounding becomes evident in its ability to expedite the growth of money compared to simple interest significantly. Compounding can occur at different frequencies: monthly, quarterly, semi-annually, or annually.
Compounding Quarterly Formula Explained
The compounding quarterly interest formula is the method in which the interest is added to the investment or loan balance. In this method of financial calculation, the process of compounding refers to accruing the interest on both the initial amount of the principal and also on any previously accumulated interest.
When the compounding of the interest is done on a quarterly basis, using the formula for compounding quarterly, it means that the interest to be paid on the loan or any fund is calculated and added to the balance after a gap of every three months. This means it is added to the balance four times in a financial year. During each time of adding the interest, the interest calculation in the subsequent period will include the interest that is newly added.
As a result of this kind of compounding, investors and lenders benefit to a huge extent. This is because quarterly compounding allows the investment to grow more frequently, and in case of a loan, there is a more frequent accrual of the outstanding balance. Thus, the return on investment is higher and faster.
By using the appropriate method or formula, it is possible to determine the future value of the investment from the compounded quarterly number, if the interest compounding is done quarterly.
How To Compute?
The formula for compounding quarterly for calculation is shown below.
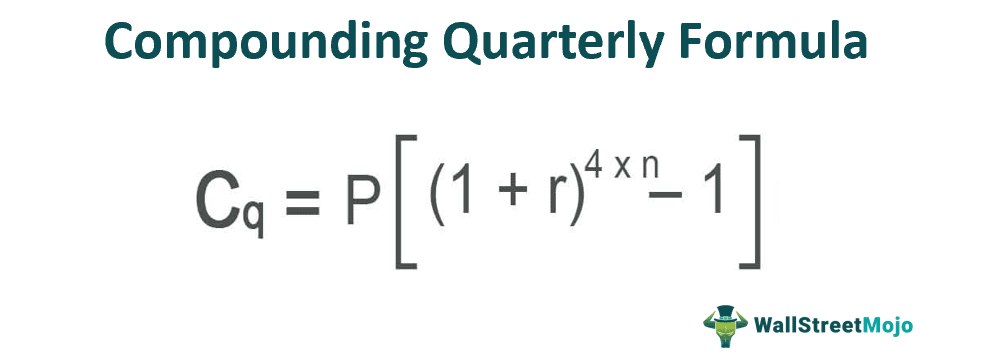
Where,
- Cq is the quarterly compounded interest
- P would be the principal amount
- r is the quarterly compounded rate of interest
- n is the number of periods
The formula for compounding quarterly is a subset of compounding formula. Here the principal amount, number of periods, and the interest rate would be required. The only modification in the compounded quarterly number is the rate of interest would be raised to n*4, which is static since we are supposed to calculate interest quarterly. Therefore, it compounds the interest quarterly, and the income grows every quarter, which is what this formula is trying to explain and get those results.
Examples
Let us understand the concept with the help of some suitable examples. However, the method for quarterly compounding formula in excel is also given below.
Example #1
Mr. Kamal deposited $50,000 in KJK bank for four years, and the bank pays 5 percent as a rate of interest, which is quarterly compounded. You are required to calculate the quarterly compounded interest.
Solution
We are given all the required variables;
- Principal Amount: 50000.00
- Rate of Interest: 5%
- Number of Years: 4.00
- Frequency: 4.00
Therefore, the calculation of quarterly compound interest will be –
- Cq = P
- = 50,000
- = 50,000
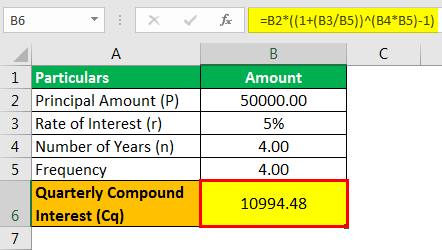
- = 10,994.48
Example #2
BCC co-operative bank has two schemes which they are evaluating the projections as to which would be more preferred by their customers. The details of both schemes are given below, as collected by the finance department.
| Particulars | Scheme I | Scheme II |
|---|---|---|
| Initial Amount to be Deposited | 200,000 | 400,000 |
| Rate of Interest | 8.50% | 8.25% |
| Minimum Lock-in Period | 6 | 7 |
| Compounded Frequency | 4 | 4 |
| Additional Benefit | Life Insurance | Medical Insurance |
The initial amount deposited includes a premium of 11,000 for scheme one, which shall not be invested, and scheme II, which is a premium of 25,000, which shall not be invested. Life Insurance covers the benefit of 1000,000, whereas the medical scheme covers the benefit of 700,000.
You are required to evaluate the benefits of the scheme.
Solution
Here, we need to compare the scheme benefits, and first, we shall calculate the quarterly compounded interest, using the compounding quarterly interest formula.
The initial amount that would be invested would be 200,000 less 11,000, which is 189,000 for scheme I, and for scheme II it would be 400,000 less 25,000, which is 375,000.
Use the following data for the calculation of quarterly compound interest.
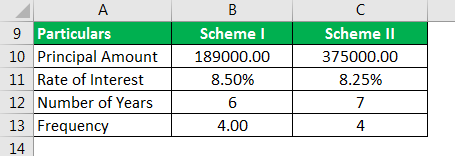
Scheme I
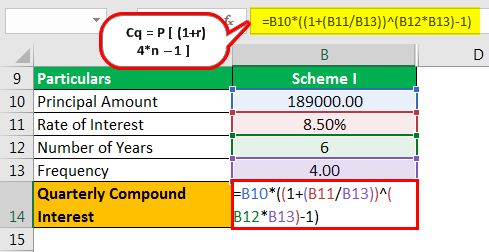
- Cq = P
- =189,000
- =189,000
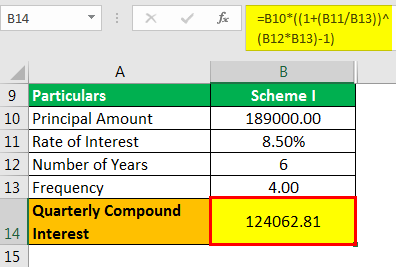
- = 1,24,062.81
Scheme II
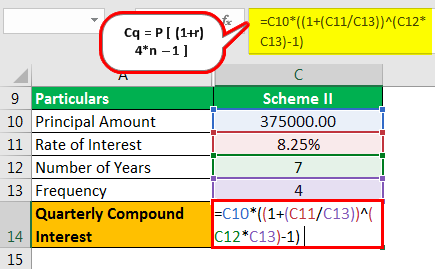
- Cq = P
- = 375,000
- = 375,000
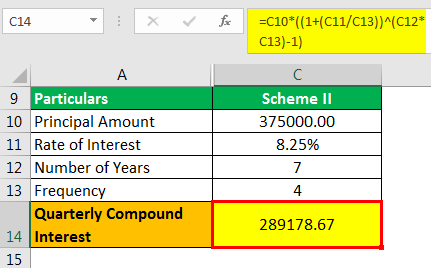
- = 2,89,178.67
It is difficult to make a decision here as we are not comparing apples to apples as one scheme is for six years, and another is for seven years. Further, if we go through policy benefits, the customer might choose scheme I as a lower investment and policy cover of 1000,000.
Example #3
SMC Municipal corporation has issued new products for capturing money from the market. Money has to be invested in two phases. In phase I, 50% will be invested, and the rest will be invested after five years. For the first five years, the rate of interest that will be paid is 8%, and for the next five years, it will be 7.5%. These will be paid quarterly. Mr. W invested 500,000 in the initial period. You are required to calculate the income earned on the investment for Mr. W.
Solution
We are given all the details here, and we can use the formula below to calculate the income derived by investing 10,000 monthly for 12 years at a rate of 11.50% compounded monthly.
Use the following data for the calculation of quarterly compound interest
| Particulars | Phase I | Phase II |
|---|---|---|
| Principal Amount (P) | 2500.00 | 2500.00 |
| Rate of Interest (r) | 8.00% | 7.50% |
| Number of Years (n) | 5 | 5 |
| Frequency | 4 | 4 |
Phase I
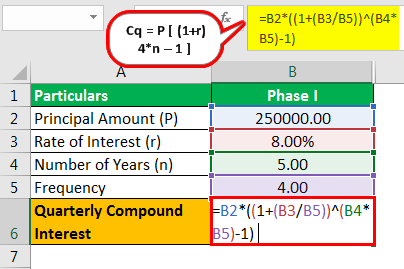
- Cq = P
- = 250,000
- = 250,000
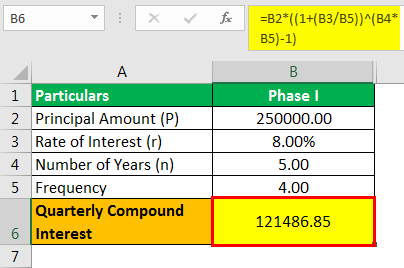
= 1,21,486.85
Phase II
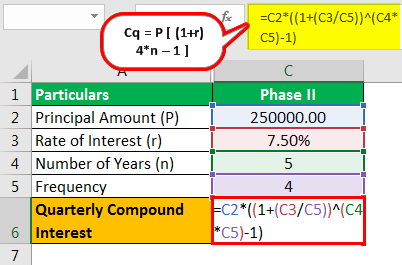
- Cq = P
- =250,000
- =250,000
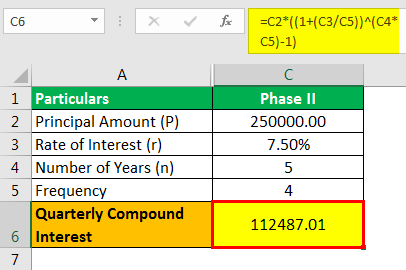
= 1,12,487.01
Total Income
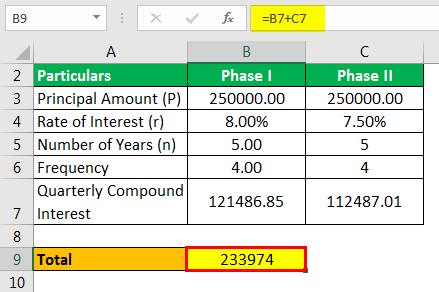
Hence, the total income earned by Mr. W on his investment will be 1,21,486.85 + 1,12,487.01, which shall be 2,33,974.
Thus, the above examples give us a clear idea about the process of compounding on a quarterly basis and along with that we also get the template of quarterly compounding formula in excel in this article.
Frequently Asked Questions (FAQs)
Compounding quarterly is often considered better than compounding annually because it results in more frequent interest calculations and reinvestments. Quarterly compounding means that interest is added to the principal every three months, allowing the interest to earn additional interest more frequently. This more frequent compounding accelerates the growth of the investment over time compared to annual compounding, where interest is added just once a year.
Compounding quarterly is divided into four intervals to align with the quarters of a year. Each interval represents three months, resulting in four compounding periods within a year. This frequency facilitates regular reinvestment of earned interest and maximizes the investment's growth.
While quarterly compounding offers benefits, it also comes with potential disadvantages. The more frequent compounding can lead to higher administrative and bookkeeping costs for financial institutions, which customers might pass on. Additionally, more frequent compounding might create a perception of higher returns, which can be misleading if not clearly communicated.
Relevance and Uses
Compounding grows the money much faster than the interest, which is earned by way of simple interest. Compounding can be monthly, quarterly, semi-annually, and annually. Most of the financial products, which include saving accounts as well, are mostly based on a quarterly or semi-annual basis.
Recommended Articles
This article has been a guide to what is Compounding Quarterly Formula. We explain it along with examples, how to compute it and its relevance and uses. You may learn more about finance from the following articles –
