Confidence Interval

A confidence interval in statistics refers to the possible range within which true values of an unknown population parameter fall. Before testing, a specific confidence level is determined. Confidence levels are represented in percentages, ranging between 80% to 99%.

Statistical analysis is conducted using sample data. Confidence interval measures the uncertainty in hypothetical testing. A narrow confidence interval is desirable; it provides a reliable and specific result.

• A confidence interval (CI) in statistics is the range of lower and upper values within which true values of a population lie.
• The margin of error is the deviation between sample values and population outcome.
• When the sample size is large, there are fewer chances of error, shrinking the standard error.
• The formula for determining lower and upper values of CI is as follows: CI = μ ± Z (σ/√n)

The confidence interval (CI) is the lower and upper limit between which the true values of the population lie—for the decided confidence level. In other words, the confidence interval determines the level of uncertainty in sample data.

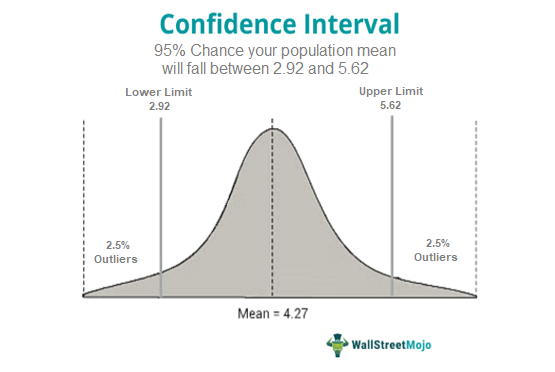
The various terminologies used while determining confidence in a sample or population are as follows:

• Sample Mean: It is the average value derived from the sum of all the sample variables divided by the total number of variables.
• Population Mean: It is derived by dividing the aggregate of all the population variables by the total number of variables in the population.
• Critical Factor: The critical value can be acquired by performing a Z-test or t-test; it helps determine the margin of error.
• Confidence Level: The confidence level is the probability of confidence interval true values resembling the population mean. Commonly used confidence levels are 90%, 95%, and 99%.
• Standard Deviation: The standard deviation determines the dispersion or spread of the data values from its mean.
• Sample or Population Size: The sample size is the total number of observations taken from the whole population for the analysis. The overall population is considered for analysis when the population size is limited.
• The margin of Error: The chances of deviation of the evaluated outcome from the actual result are also considered while determining the confidence level. The margin of error is denoted as follows:

Z (σ / √n) 

Here, Z is the Z-value, σ is the standard deviation, and n is the sample size.

In such an analysis, larger sample sizes reflect increased confidence interval accuracy. Thus, researchers can determine the value closest to the actual population mean—for large samples.

The CI can be evaluated using the following formulas:

CI = μ ± Z (σ/√n), or, CI = μ ± t (σ/√n)

In the above formula, the lower interval is computed as follows:

CI = μ - Z (σ/√n), or, CI = μ - t (σ/√n)

The upper interval is calculated as follows:

CI = μ + Z (σ/√n), or, CI = μ + t (σ/√n)

Here,

• CI is the Confidence Interval.
• μ is the mean.
• Z is the critical Z-value.
• σ is the standard deviation of the sample.
• n is the number of sample observations.
• Z (σ / √n) signifies the margin of error.
• t is the critical t-value.

The following steps facilitate the computation of CI for the given sample distribution:

1. Count the number of observations in the sample data.
2. Find the mean and standard deviation.
3. Select a confidence level—it can be 95% or 99%.
4. Determine the Z-value assigned to the preferred confidence level on the Z-table.
5. Use the CI formulas to find the lower and upper values of the CI.

Example #1

A town has approximately 10000 engineers, and the government collects sample data from 400 engineers. The government collects values of engineers’ monthly incomes. The government chose a confidence level of 90%, the mean is $5754, and the standard deviation is $415. For the given values, find the CI.

Solution:
Given:
Mean (μ) = $5754

Standard Deviation (σ) = $415

Sample Size (n) = 400

Confidence Level = 90%,

Therefore, Z-value = 1.645 (based on Z-table)

CI = μ ± Z (σ/√n)

Lower Value:

CI = μ - Z (σ/√n)

CI = 5754 – 1.645 (415 / √400) = $5720

Upper Value:

CI = μ + Z (σ/√n)

CI = 5754 + 1.645 (415 / √400) = $5788

Thus, we can say that there is a 90% possibility of an engineer earning between $5720 and $5788 in the given town.

Example #2

A medical university has ten branches within a state and a total of 16000 students. The management conducted a sample analysis on the percentage of marks secured by 100 students (10 from each branch). The mean is 78%, the confidence level is 80%, and the standard deviation is 35%. Based on given values, determine the CI.

Solution:
Given:
Mean (μ) = 78%

Standard Deviation (σ) = 35%

Sample Size (n) = 100

Confidence Level = 80%

Therefore, Z-value = 1.28 (based on Z-table)

CI = μ ± Z (σ/√n)

Lower Value:

CI = μ - Z (σ/√n)

CI = 78 – 1.28 (35 / √100) = 73.52%

Upper Value:

CI = μ + Z (σ/√n)

CI = 78 + 1.28 (35 / √100) = 82.48%

Thus, for the given university, there is an 80% probability of a medical student scoring between 73.52% to 82.48%.

Confidence Interval of 95

A confidence interval of 95 signifies that in a sample or population analysis, 95% of the true values would provide the same mean value—even if the statistical test is repeated multiple times using different sample sets.

In other words, we can say that there is a 95% probability that the true population mean lies between the lower and the upper values of the evaluated confidence interval.

Now, let us look at an example to understand the 95% confidence level:

Let us assume that a village contains a population of 15000 people. For analysis, the government chooses a sample size of 900. The government is trying to determine the average daily wage of the people. If the sample mean is computed as $37, and the standard deviation is $19.5, determine the CI for the 95% confidence level.

Solution:
Given:
Mean (μ) = $37

Standard Deviation (σ) = $19.5

Sample Size (n) = 900

Confidence Level = 95%, therefore, Z-value = 1.96 (based on Z-table)

CI = μ ± Z (σ/√n)

Lower Value:

CI = μ - Z (σ/√n)

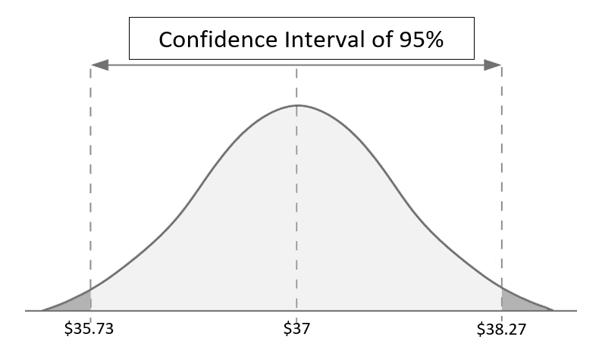
CI = 37 – 1.96 (19.5 / √900) = $35.73

Upper Value:

CI = μ + Z (σ/√n)

CI = 37 + 1.96 (19.5 / √900) = $38.27

Thus, for the given village, there is a 95% probability of a villager earning between $35.73 and 38.27 on a daily basis.

Now, let us plot this example on a CI graph:

CI varies for the degree or level of confidence as follows:

• A CI of 90%
• A CI of 95%
• A CI of 99%

However, in statistics, CI can be tested for confidence levels ranging between 80% and 99%. The selection of the confidence level in a statistical inference depends upon the sample size.

The interpretation of CI determines the degree of certainty that the population mean lies between the acquired lower and upper limits. For instance, at a 90% confidence level, there is a 90% probability of the population mean ranging between the evaluated lower and upper CI values.

This has been a guide to what is Confidence Interval & meaning. We discuss Confidence Interval 95, statistics, examples, formula, & how to calculate it? You can learn more about it from the following articles -

• Inferential Statistics
• Central Limit Theorem
• Statistical Significance