Put Call Parity Formula

The put-Call Parity formula states that the return from holding a short put and a long call option for a stock should provide an equal return as provided by holding a forward contract for the same stock. The principle applies where the options and forward contracts are of the same stock for the same strike price and expiration date.

This principle applies to European options and not to American options. European options can be exercised only on the expiry date, while American options can be exercised any time before the expiry date.

As per the Put-Call Parity principle price of a call and discounted present value of strike price should be equal to the price of the put and the stock's current market price. The relation is explained with the equation stated below:

The formula for put-call parity is:

C + PV (S) = P + MP

In the above equation, C represents the value of the call. P is the price of the put option, while MP is the stock's current market price. PV (S) is the present value of strike price discounted using a government bonds of well-developed countries, either US treasury bonds or German government bonds. Although, it does not exist because every investment has a certain amount of risk.

If the equation does not hold well, there is a scope of arbitration, i.e., risk-free profit.

Let us look at the following graph to get a better idea of put call parity. 

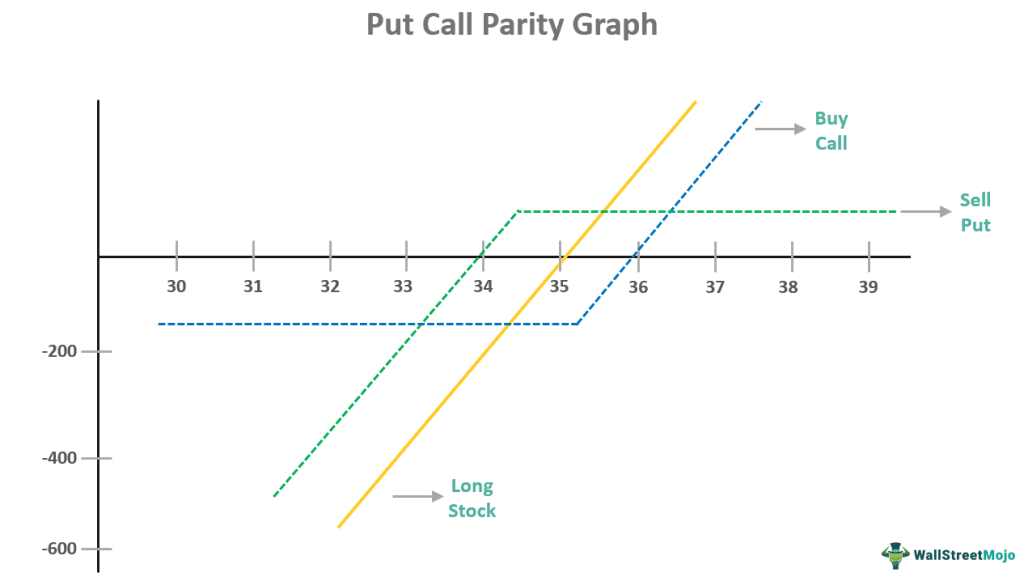
The above diagram defines the price relationship existing between a put option, the underlying stock, and a call option. The yellow line represents the long stock, while the green and blue lines denote the sell put and buy call, respectively. If a person is able to comprehend the relationship and understand how each of the components is connected, they can develop multiple synthetic positions utilizing various combinations comprising option and stock.

Example #1

Let us take an example of a stock of ABC Ltd. The share of ABC Ltd is trading at $ 93 on 1 January 2019. Call of the strike price of $ 100 for 31 December 2019 Expiry is trading at $ 8. At the same time, the risk-free interest rate in the market is 8%.

Solution:

Use the below-given data for the calculation of put-call parity.

• Market Price (MP): 93
• Call (C): 8
• Strike Price: 100
• Risk-Free Interest Rate: 8%

Therefore, to establish the put-call parity principle, the following equation should hold good:

8 + PV of 100 discounted at 8% = P + 93

i.e. 8 + 92.59 = P +93

P = 92.59 + 8 - 93

Put Call Parity equation will be –

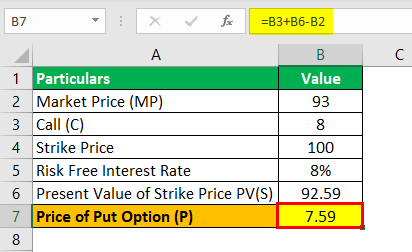
Price of put Option = 7.59

If the actual market price of the put is not equal to $ 7.59, there will be an arbitrage opportunity.

This arbitrage opportunity does not exist in a real market for long. Arbitrators in the market grab this opportunity quickly, and stock prices or options automatically adjust to establish put-call parity.

In this example, if the actual market price of the put is $ 9, the arbitrators will start selling or shorting the put, eventually increasing the supply of the put in proportion to its demand. Accordingly, the price of the put will fall to $ 7.59.

We had assumed stock price, call price, and risk-free rate in the above example and calculated the price of a put option. However, we can also take another example where the price of the put can be assumed, and any other equation component can be calculated.

Example #2

In this example, let us assume the call of stock of XYZ Ltd. The strike price of $ 350 is trading at $ 29 on 1 January 2019. The expiry date of the same is 31 December 2019. Put of the stock for the same strike price and expiry date is trading at $ 15. The risk-free interest rate in the market is 10%. Let us calculate what should be the current market price of the stock of XYZ Ltd:

Solution:

Use the below-given data for the calculation of put-call parity.

• Call (C): 29
• Strike Price: 350
• Risk Free Interest Rate: 10%
• Price of Put Option (P): 15

Calculation of Market Price can be done as follows:

C + PV (S) = P + MP

i.e. 29 + PV (350) at rate of 10% = 15 + MP

i.e. 29 + 318.18 = 15 + MP

MP = 318.18 + 29 – 15

Market Price will be -

Market Price = 332.18

If the actual market price of the stock is not equal to 332.18, there will be an arbitrage opportunity.

Example #3

In continuation of assumptions taken in example 2, If the actual market price of the stock is 350, that means either stock is trading at a higher price, the call is trading at a lower price, or the put is trading at a higher price. To earn a risk-free profit, an arbitrator will do the following:

Solution:

On 1 January 2019

He will buy a call by investing $ 29 and $ 318.18 @ a risk-free interest rate of 10% for a year. He will sell put options is $ 15 and also short sell the stock at 350.

Calculation of Net cash inflow can be done as follows:

• Call (C): 29
• Invest: 318.18
• Put: 15
• Strike Price: 350
• Net Cash Flow: 17.82

Net cash inflow in his pocket on 1 January 2019 will be 350 + 15 – 318.18 – 29.

Net Cash inflow = 17.82

Scenario #1 - Suppose on 31 December 2019, Stock is Trading at $ 390

His call will fetch $ 40. from his risk-free investment of $ 318.18, and he will get $ 350. He will not have to pay anything on the put option. However, he will have to buy the share from the current market at $ 390, which he had short-sold initially.

Calculation of Net cash outflow can be done as follow:

Net cash outflow / inflow on 31 December 2019 will be 350 + 40 – 390.

Inflow / Outflow = 0

Scenario #2 - Now, Suppose of Stock Price on 31 December 2019 is 250

In this case, his call will fetch nothing, while he will have to pay $ 100 on the put. His risk-free investment will fetch him $ 350. At the same time, he will have to buy the share from the current market at $ 250, which he had short-sold initially.

Calculation of net cash outflow can be done as follows:

Net cash outflow/inflow on 31 December 2019 will be 350 – 250 -100.

Inflow / Outflow = 0

Irrespective of the price of a stock on the expiry date, his cash flow on the said date will be 0, while he had already earned $ 17. 82 on 1 January 2019. It was because of the availability of arbitrage opportunities in the market. Very soon, the arbitrators in the market will grab this opportunity, and the stock prices and options will adjust to satisfy the put-call parity equation.

Please note that these types of arbitrage opportunities hardly exist in a mature market. Further, the transaction fee and the taxes in the real market may make it difficult or impossible to take advantage of any put-call imparity, if available. To analyze the put-call parity, prices of options and the current market price of the stock can be taken from the stock market. The interest rate provided by the government bonds can be taken as a risk-free interest rate. However, all the variables and the market rules shall be considered while analyzing the put-call parity for any particular stock.