Dickey-Fuller Test

Publication Date :

15 Apr, 2024

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Dickey-Fuller Test vs Augmented Dickey-Fuller Test

The Dickey-Fuller test and the Augmented Dickey-Fuller test serve similar purposes in determining whether a time series dataset exhibits a unit root, indicating non-stationarity. However, there are several key differences between the two. They have been listed in the table below.

Basis	Dickey-Fuller Test	Augmented Dickey-Fuller Test
1. Determines	The Dickey-Fuller test is a unit root testing process for gauging the stationarity in a time series data. It determines stationarity in time series data.	The Dickey-Fuller test is a unit root testing process for gauging the stationarity in a time series data. It determines stationarity in time series data.
2. Model	It employs a simple autoregressive model.	It employs a simple autoregressive model.
3. Efficiency	The DF test is less efficient compared to the ADF test for interpreting stationarity in large or complex data series.	The DF test is less efficient compared to the ADF test for interpreting stationarity in large or complex data series.
4. Null Hypothesis	The null hypothesis is rejected when the coefficient is not equal to 1, depicting stationarity in data.	The null hypothesis is rejected when the coefficient is not equal to 1, depicting stationarity in data.
5. Critical Values	It derives critical values from the standard Dickey-Fuller test table.	It derives critical values from the standard Dickey-Fuller test table.
6. Formula	ΔYt = α + pYt-1 + Ɛt	ΔYt = α + pYt-1 + Ɛt
7. Usability	It is a less commonly used method compared to the ADF test.	It is a less commonly used method compared to the ADF test.

Dickey-Fuller Test Meaning

The Dickey-Fuller (DF) Test refers to a statistical test used to ascertain the stationarity in an autoregressive time series model. In other words, it examines the data series for the rejection of the null hypothesis and the existence of unit root when the outcome is more negative compared to the critical value.

As the result of such statistical testing is more negative when compared to the critical value, the null hypothesis is rejected, proving the stationarity or trend-stationarity of the given time series. Also, the alternative hypothesis in this unit root testing method can vary according to the applied equation. It is a widely used metric in finance and econometrics.

Key Takeaways

The Dickey-Fuller (DF) test refers to a unit root test that facilitates the identification of stationarity in a given time series data.
If the resulting test statistic is not as negative as the critical value, the null hypothesis is rejected, interpreting the unit root presence in the data. However, the null hypothesis is rejected.
Conversely, the Augmented Dickey-Fuller (ADF) test is the extended and improved form of the DF test, which provides a more reliable outcome when the data is of high order, complex, or extensive.

Dickey-Fuller Test In Finance Explained

The Dickey-Fuller Test for stationarity is frequently employed in finance to ensure that the critical statistical properties, such as mean and variance, in time series data remain constant over time. This assumption is inevitable for accurate financial modeling and forecasting.

It enables the comprehensive examination of past trends in finance and confirms whether these trends remain relevant as markets move forward. Also, if data lacks stationarity, the testing undertaken as part of financial modeling and forecasting may give unreliable results.

By determining stationarity, the Dickey-Fuller test assists analysts in determining whether data transformation, such as differencing, is necessary to prepare the data for further analysis or modeling. When dealing with stationary data, trading signals are formulated on the assumption that stock prices will eventually revert to the mean. This allows for capitalizing on price deviations from the mean within short time frames.

The Dickey-Fuller test was developed by American statisticians David Dickey and Wayne Fuller in 1979. Since then, it has served as a fundamental method for detecting whether the data has a unit root, which is crucial for assessing its stationarity.

It has been widely used for trending time series like asset prices. However, many economic and financial time series are more complex than the simple autoregressive models. Therefore, the duo extended this model to eliminate the various limitations and came up with the Augmented Dickey-Fuller (ADF) Test, which provides a more comprehensive analysis for extensive and high-order data. It must be noted that both DF and ADF work well when data is linear, indicating that data nonlinearity may skew the results.

Formula

Unit root testing in statistics is essential for analyzing the stationarity of data, which is a prerequisite for various statistical testing measures. The Dickey-Fuller test calculation involves the use of the following equation:

ΔY_t = α + pY_t-1 + Ɛ_t ; H₀: p = 1 → implies that the data is non-stationary

H₁: p ≠ 1 → depicts that the data is stationary

Where,

Yt is the given data;
α is the drift or intercept constant;
p is the coefficient signifying the unit root;
Y_t-1 is the value at lag of 1 in the time series;
Ɛ_t is the error term or noise

The Dickey-Fuller test interpretation involves the rejection of the null hypothesis to prove the stationarity of data.

Examples

Moving ahead, let us understand the Dickey-Fuller test for stationarity through some examples.

Example #1

Let us consider the following graph depicting the month-on-month performance of Starlight Corp’s stock.

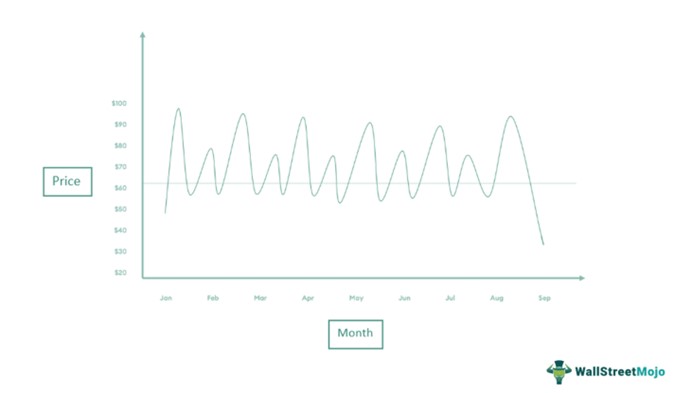
Starlight Corp’s stock graph — *You are free to use this image on your website, templates, etc..* *Please provide us with an attribution link.*

Dickey-Fuller test Interpretation: One can visually identify that the time series is stationary. Thus, on conducting the DF test, they have a coefficient of less than 1, signifying the rejection of the null hypothesis, i.e., the data has the presence of a unit root.

Example #2

Suppose Jenny, a market researcher, wants to interpret the next month's potential performance of the stock of WinFin Ltd. using the Autoregressive Integrated Moving Average (ARIMA) model.

She acquires the sample data for the last 3 months and uses it to evaluate future stock prices. However, to ensure that the time series data is stationary, Jenny performs the DF test and records the results. Thus, the unit root test enabled her to ensure that the data was predictable and relevant in the future.