Sine and cosine waves have many similarities and key differences, including their phase shift and graphical representation.
Table Of Contents
Sine Wave vs Cosine Wave
| Basis | Sine wave | Cosine wave |
|---|---|---|
| 1. Phase shift | The wave starts at zero amplitude and reaches its maximum positive value at π/2, | The cosine wave starts at its maximum positive value and reaches zero at π/2. In other words, the cosine wave is a shifted version of the sine wave. |
| 2. Graphical Representation | The sine wave graph is a smooth curve oscillating between positive and negative values. Also, the maximum and minimum values occur at regular intervals. | The graph of a cosine wave is also a smooth curve that oscillates between positive and negative values, but it is shifted by 90 degrees (π/2 radians) relative to the sine wave. |
What Is A Sine Wave?
A sine wave is a type of waveform that can be defined by the mathematical function sin(x), where x is the angle in radians. Essentially, it is a smooth and repetitive oscillation that oscillates around a central axis, and it can be described mathematically in terms of its frequency and amplitude.
A sine wave is a mathematical curve that represents a smooth periodic oscillation. It is used in technical analysis as part of charting methods to identify trends, support and resistance levels, and potential turning points in the market. The repeating pattern of peaks and troughs in a sine wave allows analysts to visually assess the cyclical nature of market data and make informed decisions based on historical patterns.
Key Takeaways
- A sine wave is a mathematical curve that represents a smooth periodic oscillation.
- It is named after the sine function, which generates a wave with a repeating pattern of peaks and troughs resembling a sine curve.
- Sine waves are used in technical analysis to identify trends, support levels, resistance levels, and potential turning points in the market. In addition, they help analysts visualize and analyze recurring patterns in financial data.
- Sine waves are applied to represent cyclical fluctuations in the value of securities, interest rates, economic indicators, and other market phenomena. They capture the repetitive nature of these phenomena over time.
Sine Wave Explained
Sine waves or sinusoidal waves are used to represent cyclical fluctuations in the value of securities and assets over time, as well as periodic variations in interest rates and economic indicators. In finance, sine waves find common applications in technical analysis. For example, analysts utilize charts and indicators, including sine waves, to identify trends, support levels, resistance levels, and potential market turning points.
Financial markets exhibit recurring patterns, and sinusoidal waves help capture these cyclical behaviors. As a result, analysts can use sinusoidal waves to identify and predict future market movements by analyzing past performance. Sinusoidal waves also play a role in financial modeling, allowing for the description of volatility patterns in different financial instruments. This aids in developing accurate predictions of interest rates and designing market-resistant financial products.
In summary, sinusoidal waves are a valuable tool in finance, enabling analysts to understand and forecast the cyclical patterns observed in financial markets. Analysts can enhance their models by leveraging sinusoidal waves, making more accurate predictions, and creating financial instruments that align with investors' needs.
Formula
The formula for a sine wave is :
y = A sin (ωt + φ)
Where:
- y is the instantaneous value of the wave
- A is the amplitude of the wave
- ω is the angular frequency of the wave, which is equal to 2π times the frequency f of the wave, i.e., ω = 2πf
- t is the time
- φ is the phase angle of the wave, which represents the offset of the wave from a reference position at t = 0.
In simpler terms, the formula represents a wave oscillating sinusoidally with an amplitude of A and a frequency of f. The phase angle φ determines the starting point of the wave, and the angular frequency ω determines the rate of change of the wave over time. The sinusoidal wave is periodic and repeats itself after a certain interval, known as the period T, which equals 1/f.
Applications
Here are two simple examples showcasing the application of sine waves in finance:
- Stock Price Movements: The price of a particular stock often exhibits cyclical behavior over time. Analysts can plot a sinusoidal wave by analyzing historical price data to represent the periodic fluctuations in the stock's value. This can help identify the peaks and troughs, enabling investors to make informed decisions about buying or selling the stock based on the expected continuation or reversal of the trend.
- Interest Rate Cycles: Interest rates tend to fluctuate in cycles, moving between periods of expansion and contraction. Analysts can use a sinusoidal wave model to represent the periodic variations in interest rates over time. This allows for a better understanding of the interest rate cycle and assists in predicting future changes. Financial institutions can use this information to develop suitable products, such as adjustable-rate mortgages or fixed-income investments that align with the anticipated interest rate trends.
Graph
A sine wave graph visualizes the mathematical function y = sin(x), where x represents the angle in radians and y represents the wave's amplitude. The sine wave graph:
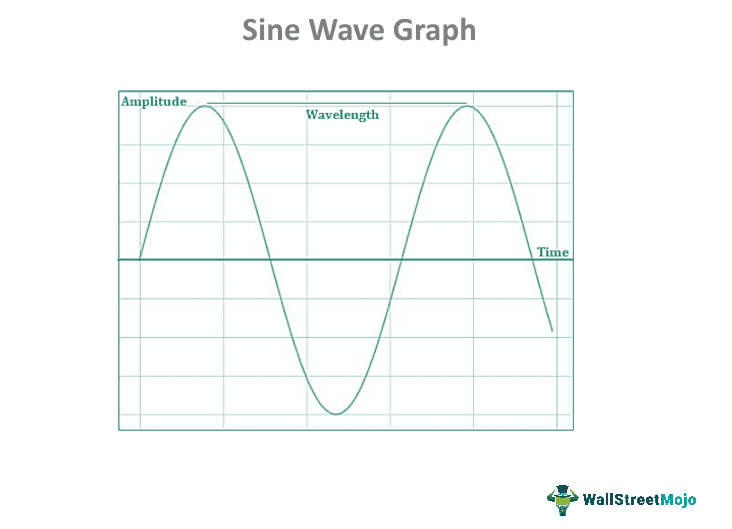
The graph appears as a smooth curve oscillating between positive and negative values, with the maximum and minimum values occurring at regular intervals.
