Expected Shortfall

What Is Expected Shortfall?

The Expected Shortfall (ES), or Conditional Value at Risk (CVaR) refers to a risk assessment tool whereby the analyst determines the amount of risk involved in an investment or portfolio. The risk might be beyond a certain confidence level or the Value at Risk threshold, in case of extreme market condition.

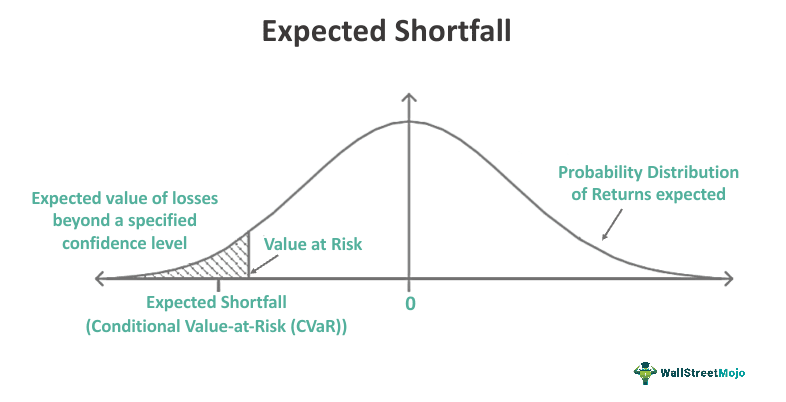
Although the chances of a worst-case scenario are rare, they are quite possible in the financial markets. Hence, it is often advisable to take calculative risks while investing and managing portfolios worth millions of dollars. CVaR is one such metric that helps institutions and fund management companies preserve capital by gauging market volatility and uncertainties over the period past the VaR limit.

• Expected Shortfall or Conditional Value-at-Risk (CVaR) is a risk measure employed to evaluate potential tail losses beyond a specific confidence level in the event of poor investment or portfolio performance.
• Risk managers and investors often prefer CVaR over VaR because of its ability to analyze tail risk and downside potential more comprehensively.
• The expected shortfall formula of ES is:

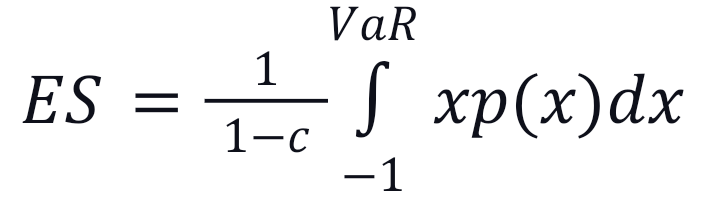
• However, it has certain limitations, such as being based on assumptions and historical data, lacking universality, providing incorrect estimation, and needing to have regulatory standardization.

Expected Shortfall Explained

Expected Shortfall (ES), also known as Conditional Value at Risk (CVaR), is a risk measure used to assess the level of risk possessed by an investment or portfolio, given that the loss exceeds the VaR. It is used in different financial organizations such as banks, mutual funds, insurance companies, hedge funds, pension funds, and endowments. Moreover, the CVaR-based portfolio optimization frameworks like the Min-CVaR, Mean-CVaR, and CVaR constrained optimization are employed in portfolio management to estimate portfolio risk, maximize returns and keep the expected shortfall low.

Large-cap stocks, like blue-chip stocks, have very low CVaR since they are less volatile. However, the small and medium-cap securities have a high expected shortfall, sometimes even higher than the VaRs. Also, most portfolios with significant CVaRs offer huge returns, although at the cost of considerable risk appetite.

CVaR offers an efficient and complete evaluation of risk compared to VaR alone. Considering the severity of losses beyond the VaR level provides a deeper understanding of potential downside risk. Financial institutions, portfolio managers, and risk analysts extensively employ this risk measure to assess investment risk, make informed decisions about risk management strategies, and determine asset allocation. Further, it aids in risk monitoring, budgeting, and reporting. Hence, the tail loss is a crucial input for financial institutions for scenario analysis, stress testing, and asset allocation.

How To Calculate?

The expected shortfall estimates the average losses incurred beyond the VaR level. Its computation involves determining the VaR (Value-at-Risk) initially. VaR represents the maximum potential loss at a designated confidence level, typically expressed as a percentage or a dollar investment amount. Following the determination of VaR, the expected shortfall is computed by averaging losses that exceed the VaR. The other essential inputs are:

• The returns distribution shape.
• Data periodicity.
• Cut-off level.
• Assumptions about the volatility of the securities.

The expected shortfall formula is:

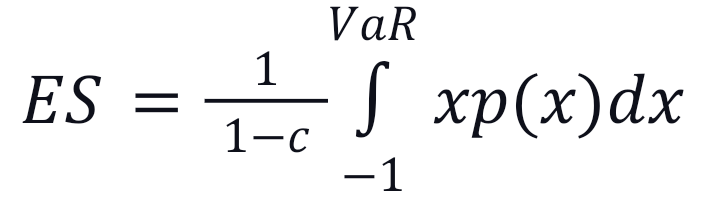
Where,

• p(x)dx is the probability density of getting “x” return;
• c is the VaR cut-off point or breakpoint;
• VaR is the evaluated Value at the Risk level.

Examples

Some of the examples are the following:

Example #1

Consider a portfolio with a confidence level of 95% VaR where the stock price will not go beyond -$1.7 in a day. However, the same portfolio with a 98% ES or CVaR suggests that there is a possibility of a 2% tail loss if the worst-case scenario occurs where the stock price may go down by -$2.1.

Example #2

Imagine Jenna is an economist advising a government on two different economic policies. Policy A is a well-established approach with known limitations, while Policy B is a new and untested strategy. Both policies have the same initial projection of potential economic losses. However, when she analyzes them with Expected Shortfall (ES), she finds that for Policy A, the expected losses, if they occur, are manageable and well understood.

In contrast, Policy B, when assessed with ES, indicates that potential losses, if realized, could be more severe, suggesting a higher level of uncertainty and potential risk. ES allows Jenna to consider not just the likelihood of losses but also their expected magnitude, aiding in making informed economic policy decisions.

Advantages And Disadvantages

Some of the important advantages and disadvantages are as follows:

Advantages

• Widely Used in Quantitative Finance: CVaR (Expected Shortfall) is a widely used measure in quantitative finance for risk management.
• Comprehensive Assessment of Tail Risk: It provides a more comprehensive assessment of tail risk than other measures like VaR by considering the entire distribution of losses beyond a specific threshold for capturing extreme events.
• Better Understanding of Loss Severity: CVaR offers additional information, such as the average loss, given that the loss exceeds the VaR threshold. This enables risk managers to understand the potential severity of losses better.
• Capital Allocation Incentives: It incentivizes risk managers to allocate capital to assets or portfolios with lower expected shortfall values, promoting better risk management.
• Diversification and Risk Reduction: CVaR encourages diversification and helps reduce concentration risk by allocating capital to different assets based on risk profiles.
• Sub-Additivity: ES is sub-additive, which means the CVaR of the overall portfolio is either equal to or less than the sum of the individual underlying asset's CVaRs.
• Suitable for Non-Normal Distributions: It is a potent risk measure suitable for distributions with fat tails and non-normal characteristics.

Disadvantages

• Complex Computation: Determining the expected shortfall for significant investment portfolios is tedious and complex, requiring extensive computation.
• Lack of Accuracy: CVaR lacks accuracy since it is based on probability distribution assumptions about the tail behavior of the loss distribution. Different models and assumptions can lead to different expected shortfall estimates, potentially failing to represent true tail risk.
• Lack of Universality: CVaR is not as universally applied in industry practices and regulatory frameworks, leading to inconsistencies.
• Dependence on Data Quality: The estimation accuracy of CVaR relies on the availability and quality of historical data. Adequate data and correct assumptions are necessary for reliable expected shortfall estimates.
• Regulatory Reporting Challenges: CVaR needs a standardized regulatory framework, which can create compliance and regulatory reporting challenges since different institutions may employ different methodologies and assumptions to calculate CVaR.

Expected Shortfall vs Value At Risk

Expected shortfall and Value at Risk (VaR) are the risk measures commonly used in finance and investment management. Although they are related, they have distinct characteristics.

Basis	Expected Shortfall	Value at Risk
Definition	ES calculates the magnitude of portfolio risk given that the loss exceeds the VaR level or threshold.	VaR represents the highest potential loss within a specified confidence level over time.
Interpretation	A comprehensive measure of tail risk that considers the worst possibilities or conditions.	Calculates the portfolio risk within the confidence level while disregarding the magnitude of losses beyond that threshold.
Mathematical Properties	A coherent risk measure with enhanced mathematical properties as it is a convex and continuous function.	Less competent mathematical properties, such as being a discontinuous function.
Sensitivity to Tail Risk	Places more emphasis on extreme events and provides a measure of the average severity of losses in the tail.	Sensitive to extreme events but does not provide explicit information about the severity of losses outside the VaR level.
Optimization	It can be optimized for implementing linear programming and convex methods for better risk assessment and management.	Challenging to optimize for solving complex problems.
Risk Management	Portfolio managers employ it to assess, monitor, budget, and report an investment portfolio's potential tail loss and associated risk.	Investors use it to assess the minimum loss possibility and devise investment strategies accordingly.

Frequently Asked Questions (FAQs)

Recommended Articles

This article has been a guide to what is Expected Shortfall. We compare it with Value At Risk, explain how to calculate it, its examples, advantages, & disadvantages. You may also find some useful articles here -

• Distortion Risk Measure
• Extreme Value Distribution
• Extreme Value Theory