Portfolio Optimization

Portfolio optimization is nothing but a process where an investor receives the right guidance concerning the selection of assets from the range of other options, and in this theory, projects/programs are not valued on an individual basis; rather, the same is valued as a part of a particular portfolio.

Portfolio Optimization is good for those investors who want to maximize the risk-return trade-off since this process is targeted at maximizing the return for every additional unit of risk taken in the portfolio. The managers combine a combination of risky assets with risk-free assets to manage this trade-off. The ratio of risky assets to risk-free assets depends on the risk the investor wants to take. The optimal portfolio does not give a portfolio that would generate the highest possible return from the combination. It just maximizes the return per unit of risk taken. The Sharpe ratio of this portfolio is the highest.

• Portfolio optimization receives guidance as an investor to choose the most suitable assets from various options. The theory values projects/programs as part of a specific portfolio rather than individually.
• Asset allocation for an optimal portfolio is a two-part process: selecting asset classes and choosing assets within the category.
• Portfolio optimization balances risk and return by combining risky and safe investments in a ratio that matches the investor's risk tolerance. The most optimal portfolio has the highest Sharpe ratio, maximizing profit relative to the risk taken.

The process of portfolio optimization involves selection of such a set of asset and designing a portfolio for investment purpose that it meets the basic return objective, expected within the time period by incurring minimum cost and risk. It is a basic skill that every investor or any financial advisor, who is entrusted with the job of managing a portfolio on behalf of their client, should possess.

Portfolio optimization theory requires a lot of analysis, reviews and continuous tracking of the financial market in order to understand the performance of the asset classes, which helps in designing a strategy and make necessary adjustments that will optimize returns. It is a process of optimising the asset allocation to get the highest possible return that will be within the tolerable risk level. This ensures a balanced portfolio through proper diversification.

An optimal portfolio is said to have the highest Sharpe ratio, which measures the excess return generated for every unit of risk taken.

There are a variety of assets that are traded in the financial market and each have separate risk and return levels which include risky as well as fixed income portfolio optimization. The factors influencing them are also different. It is necessary for investors to understand the assets well to ensure optimization of the portfolio

Asset Allocation for an optimal portfolio is essentially a two-part process:

1. Selecting Asset Classes - Portfolio managers first choose the asset classes they want to allocate funds to, then decide the weight of every asset class included. Common asset classes include Equities, Bonds, Gold, and Real Estate.
2. Selecting Assets within Class - After deciding the asset classes, the manager decides how much of a particular stock or a bond she wants to include in the portfolio. The Efficient Frontier represents the risk-return relationship of an efficient portfolio on a graph. Each point on this curve represents an efficient portfolio.

There are a number of methods or portfolio optimization models used by analysts to establish a balance between the assets of a portfoilio and earn maximum return. Here are some of them.

• Modern Portfolio Theory (MPT) - Portfolio optimization is based on Modern Portfolio Theory (MPT). The MPT is based on the principle that investors want the highest return for the lowest risk. To achieve this, assets in a portfolio should be selected after considering how they perform relative to each other, i.e., they should have a low correlation. Any optimal portfolio based on the MPT is well-diversified to avoid a crash when a particular asset or asset class underperforms.

• Mean- Variance – This is a part of the above theory, where the optimization process focus on getting the bst possible return but minimizing and variation or deviation from the variance of the portfolio. The best asset allocation can be picked by making a trade-off between risk and return.
• Monte-Carlo Simulation – This is a method of simulating different types of portfolios and assessing their outcomes. Different types of inputs are used like the assets, their correlation and fluctuation in prices. This helps in identifying the possibility or level of risk and return that can be expected.
• Risk Parity – In this method of or portfolio optimization models, the aim is to achieve the risk level that is equal for all the asset class or security. Here the assets are allocated after evaluating their risk levels not their return levels. It leads to a creation of a more stable asset portfolio.
• Black-Litterman Model – It is a very useful method. It first takes into consideration the investor’s expectation of the return levels and then use that view to design a portfolio which will give the best return. Investors who understand different asset classes well and can form strong opinions, find this process very useful.

Thus, the above are some widely used methods for optimization of portfolio for investors. However, all of them have their own pros and cons, which should be carefully studied before application.

Let’s see some practical examples of enhanced portfolio optimization to understand it better.

Example #1

If we take an example of Apple and Microsoft based on their monthly returns for the year 2018, the following graph shows the Efficient Frontier for a portfolio consisting only of these two stocks:

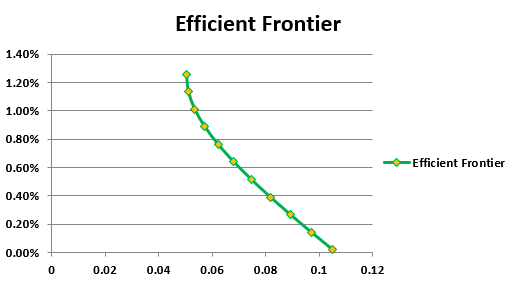
The X-axis is the standard deviation, and the y-axis is the portfolio return for the level of risk. If we combine this portfolio with a risk-free asset, the point on this graph where the Sharpe ratio is maximized represents the optimal portfolio. It is the point at which the capital allocation line is tangential to the efficient frontier. The reason behind this is that at that point, the Sharpe ratio (which measures the increase in expected return for every additional unit of risk taken) is the highest.

Example #2

Suppose we want to combine a risky portfolio having only BestBuy and AT&T stocks and a risk-free asset with a return of 1%. We will plot the Efficient Frontier based on the return data for these stocks and then take a line that starts at 1.5 on the Y-axis and is tangential to this Efficient Frontier.

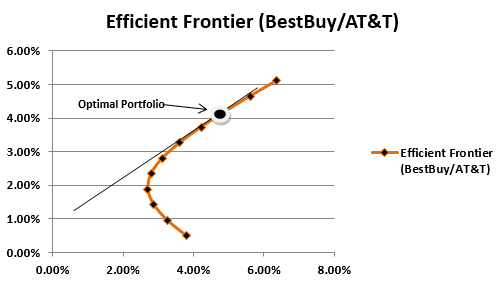
The X-axis represents the Standard Deviation, and Y-axis represents the return of the portfolio. An investor who wishes to take on less risk can move to the left of this point, and high risk-taking investors can move to the right. An investor who does not wish to take any risk at all would invest all the money in the risk-free asset but, simultaneously, limit their portfolio return to 1%. An extra return will be earned by taking the risk.

Below mentioned are some of the major advantages of portfolio optimization:

• Maximizing Return - The first and foremost objective of portfolio optimization is maximizing return for a given level of risk. The risk-return trade-off is maximized at the point on the efficient frontier that represents the optimal portfolio. So managers pursuing the process of portfolio optimization are often able to achieve high returns per unit of risk for their investors. This helps with client satisfaction.
• Diversification - Optimal Portfolios are well diversified in order to do away with the unsystematic risk or non-priced risks. Diversification of risky or fixed income portfolio optimization helps in protecting investors against the downside in case a particular asset underperforms. The other assets in the portfolio will protect the investor’s portfolio from crashing, and the investor stays in a comfortable zone.
• Identifying Market Opportunities - When managers indulge in active portfolio management, they track a lot of market data and update themselves with the markets. This practice can help them identify opportunities in the market ahead of others and take advantage of those opportunities for the benefit of their investors.
• Risk management – The various models used, aim to minimise the risk level. This allows the investors to remain within the risk tolerance levels and at the same time design an asset portfolio that is best suited for them. The idea is to identify the mix of assets of securities that suit the return expectation, risk tolerance and time horizon of the investor.
• Efficiency in allocation – Since the process aims at evaluation of fluctuation in the market,   and also identifying deviation in performance, this leads to an efficient level of capital allocation that is best for the investor.

Below mentioned are some of the major limitations of portfolio optimization:

• Frictionless Markets - The Modern Portfolio Theory, on which the concept of portfolio optimization is based, makes certain assumptions hold. One of the assumptions is that the markets are frictionless, i.e., there are no transaction costs, constraints, etc., that prevail in the market. In reality, this is often found not to be true. There are frictions in the market, and this fact makes the application of modern portfolio theory complicated.
• Normal Distribution - Another assumption under the modern portfolio theory is that the returns are normally distributed. It ignores the concepts of skewness, kurtosis, etc., when using the return data as inputs. It is often found that the returns are not normally distributed. This assumption violation under the modern portfolio theory makes it challenging to use.
• Dynamic Coefficients - The coefficients used in the data for portfolio optimization, such as the correlation coefficient, can change as the market situations change. The assumption that these coefficients stay the same might not be true in all cases.
• Input sensitive – The entire process is very sensitive to inputs. In case of a very small change in a parameter like the return expectation, the entire portfolio will be impacted. As a result, the models may not produce the best results.
• Compexity – Sometimes the models of portfolio optimization theory and the procedures may become too complex to handle due to many assets or securities included in it. They may require very advanced techniques and this again creates room for error. There may be overfitting of past data an thus, the allocation may not be proper.
• External factors – There are al lot of external elements like geopolitical events, unforeseen contingencies, sudden changes in rules and regulations that greatly affect asset correlation and prices. This affects the portfolio optimization. There is also a cost involved in execution of the process, which are very practical scenarios and affect the optimization strategy greatly.

Thus, the above are some important advantages and limitation of the concept enhanced portfolio optimization. Investors should understand them so as to use the concept in an effective manner.

This has been a guide to what is Portfolio Optimization. We explain the methods, with examples, process, advantages and limitations. You can learn more about portfolio management from the following articles –

• Examples of Standard Deviation
• Formula of Portfolio Variance
• Career Options in Portfolio Management
• Compare - Portfolio Management vs Investment Banking