Multiple Regression Formula

What is a Multiple Regression Formula?

Multiple regression formula is used in the analysis of relationship between dependent and multiple independent variables and formula is represented by the equation Y is equal to a plus bX1 plus cX2 plus dX3 plus E where Y is dependent variable, X1, X2, X3 are independent variables, a is intercept, b, c, d are slopes, and E is residual value.

y = mx1 + mx2+ mx3+ b

Where,

Y= the dependent variable of the regression
M= slope of the regression
X1=first independent variable of the regression
The x2=second independent variable of the regression
The x3=third independent variable of the regression
B= constant

Explanation of Regression Analysis Formula

Multiple Regressions are a method to predict the dependent variable with the help of two or more independent variables. While running a this analysis, the main purpose of the researcher is to find out the relationship between the dependent variable and the independent variables. In order to predict the dependent variable, multiple independent variables are chosen which can help in predicting the dependent variable. It is used when linear regression is not able to do serve the purpose. Regression analysis helps in the process of validating whether the predictor variables are good enough to help in predicting the dependent variable.

Examples

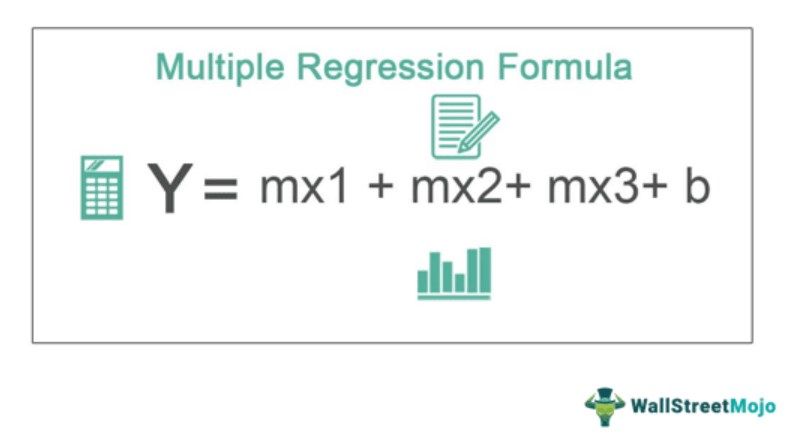
You can download this Multiple Regression Formula Excel Template here – Multiple Regression Formula Excel Template

Example #1

Let us try and understand the concept of multiple regressions analysis with the help of an example. Let us try to find out what is the relation between the distance covered by an UBER driver and the age of the driver and the number of years of experience of the driver.

For the calculation of Multiple Regression go to the Data tab in excel and then select the data analysis option. For the further procedure and calculation refers to the given article here – Analysis ToolPak in Excel

The regression formula for the above example will be

y = MX + MX + b
y= 604.17*-3.18+604.17*-4.06+0
y= -4377

In this particular example, we will see which variable is the dependent variable and which variable is the independent variable. The dependent variable in this regression equation is the distance covered by the UBER driver and the independent variables are the age of the driver and the number of experiences he has in driving.

Popular Course in this category

All in One Financial Analyst Bundle (250+ Courses, 40+ Projects)4.9 (1,067 ratings) 250+ Courses | 40+ Projects | 1000+ Hours | Full Lifetime Access | Certificate of Completion

View Course

Example #2

Let us try and understand the concept of multiple regressions analysis with the help of another example. Let us try to find out what is the relation between the GPA of a class of students and the number of hours of study and the height of the students.

For the calculation, go to the Data tab in excel and then select the data analysis option.

The regression equation for the above example will be

y = MX + MX + b

y= 1.08*.03+1.08*-.002+0

y= .0325

In this particular example, we will see which variable is the dependent variable and which variable is the independent variable. The dependent variable in this regression is the GPA and the independent variables are study hours and height of the students.

Example #3

Let us try and understand the concept of multiple regressions analysis with the help of another example. Let us try to find out what is the relation between the salary of a group of employees in an organization and the number of years of experience and the age of the employees.

For the calculation, go to the Data tab in excel and then select the data analysis option.

The regression equation for the above example will be

y = MX + MX + b
y= 41308*.-71+41308*-824+0
y= -37019

In this particular example, we will see which variable is the dependent variable and which variable is the independent variable. The dependent variable in this regression equation is the salary and the independent variables are the experience and age of the employees.

Relevance and Use

Multiple regressions is a very useful statistical method. Regression plays a very role in the world of finance. A lot of forecasting is done using regression analysis. For example, the sales of a particular segment can be predicted in advance with the help of macroeconomic indicators that has a very good correlation with that segment.