Residual sum of squares

Residual Sum of Squares (RSS) is a statistical method that helps identify the level of discrepancy in a dataset not predicted by a regression model. Thus, it measures the variance in the value of the observed data when compared to its predicted value as per the regression model. Hence, RSS indicates whether the regression model fits the actual dataset well or not. 

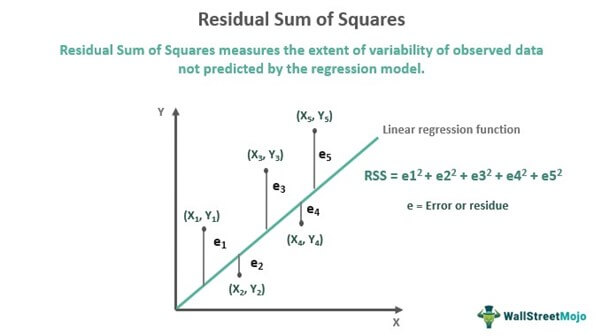
Also referred to as the Sum of Squared Errors (SSE), RSS is obtained by adding the square of residuals. Residuals are projected deviations from actual data values and represent errors in the regression model’s estimation. A lower RSS indicates that the regression model fits the data well and has minimal data variation. In finance, investors use RSS to track the changes in the prices of a stock to predict its future price movements.

• Residual Sum of Squares (RSS) is a statistical method used to measure the deviation in a dataset unexplained by the regression model.
• Residual or error is the difference between the observation's actual and predicted value.
• If the RSS value is low, it means the data fits the estimation model well, indicating the least variance. If it is zero, the model fits perfectly with the data, having no variance at all.
• It helps stock market players to assess the future stock price movements by monitoring the fluctuation in the stock prices.

RSS is one of the types of the Sum of Squares (SS) – the rest two being the Total Sum of Squares (TSS) and Sum of Squares due to Regression (SSR) or Explained Sum of Squares (ESS). Sum of squares is a statistical measure through which the data dispersion is assessed to determine how well the data would fit the model in regression analysis.

While the TSS measures the variation in values of an observed variable with respect to its sample mean, the SSR or ESS calculates the deviation between the estimated value and the mean value of the observed variable. If the TSS equals SSR, it means the regression model is a perfect fit for the data as it reflects all the variability in the actual data.

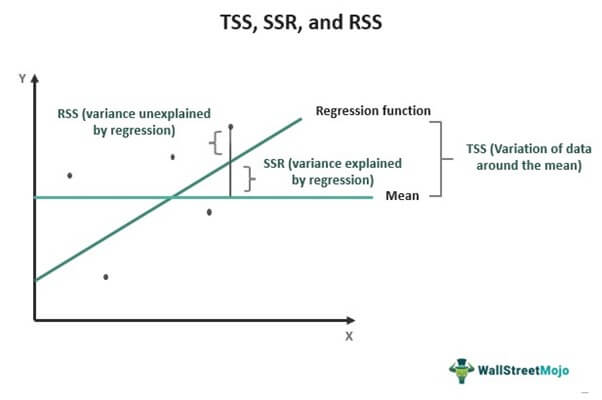
On the other hand, RSS measures the extent of variability of observed data not shown by a regression model. To calculate RSS, first find the model's level of error or residue by subtracting the actual observed values from the estimated values. Then, square and add all error values to arrive at RSS.

The lower the error in the model, the better the regression prediction. In other words, a lower RSS signifies that the regression model explains the data better, indicating the least variance. It means the model fits the data well. Likewise, if the value comes to zero, it’s considered the best fit with no variance.

Note that the RSS is not similar to R-Squared. While the former defines the exact amount of variation, R-squared is the amount of variation defined with respect to the proportion of total variation.

The discrepancy detected in the data set through RSS indicates whether the data is a fit or misfit to the regression model. Thus, it helps stock market players to understand the fluctuation occurring in the asset prices, letting them assess their future price movements.

Regression functions are formed to predict the movement of stock prices. But the benefit of these regression models depends on whether they well explain the variance in stock prices. However, if there are errors or residuals in the model unexplained by regression, then the model may not be useful in predicting future stock movements.

As a result, the investors and money managers get an opportunity to make the best and most well-informed decisions using RSS. In addition, RSS also lets policymakers analyze various variables affecting the economic stability of a nation and frame the economic models accordingly.

Here is the formula to calculate the residual sum of squares:

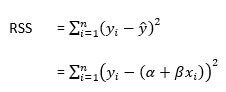
Where,

Let’s consider the following residual sum of squares example based on the set of data below:

The absolute variance can be easily found out by implementing the above RSS formula:

          = {1 - }² + {2 - }² + {6 - }² + {8 - }²

            = 0+1+1+1 = 3

This has been a guide to what is Residual Sum of Squares. Here we explain how to calculate residual sum of squares in regression with its formula & example. You can learn more about it from the following articles – 

• Least Squares Regression
• Gradient Boosting
• Regression Line