Heteroskedasticity

The heteroskedasticity test refers to ununiform variance in a sequence of variables. It is also referred to as an error. Ideally, researchers want homoskedasticity or homogeneity in variance. A homogenous variance explains a researcher’s assumption.

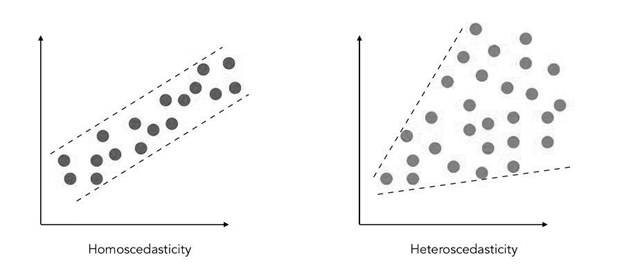
A cone-like shape is seen when heteroskedastic dispersion is plotted on a graph. This depicts errors in variance. Most real-world data exhibit heteroskedasticity. An unequal scatter is more likely—this becomes a problem for regression assumptions. Researchers alter the statistical model in an attempt to find better results.

• Heteroskedasticity generally refers to an unequal scattering of data points. As a result, the observed values deviate from the predicted values ununiformly.
• There are two subtypes, pure and impure heteroskedastic dispersion. Such statistical errors are common for large ranges and cross-sectional studies.
• Heteroskedastic dispersion diminishes the coefficient of variation accuracy—analysts must rework or improve their model to define more accuracy.
• Some regression models are prone to heteroskedastic dispersion. Analysts try to solve such errors by changing the dependent variable.

Heteroskedasticity is Greek for data with a different dispersion. For example, in statistics, If a sequence of random variables has the same finite variance, it is called homoskedastic dispersion; if a sequence does not have the same variance, it is known as heteroscedastic dispersion.

Dispersion is a means of describing the extent of distribution of data around a central value or point. Lower dispersion indicates higher precision in data measurements, whereas higher dispersion means lower accuracy.

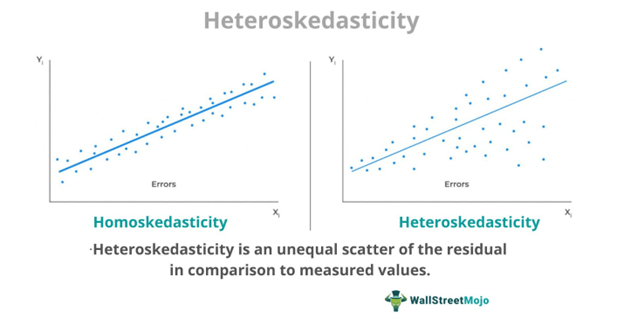
A residual spread is plotted on a graph to visualize the correlation between data and a particular statistical model. If the dispersion is heteroscedastic, it is seen as a problem. Researchers look for homoskedasticity. The data points should have a constant variance to satisfy the researcher's assumption.

In residual plots, heteroskedasticity in regression is cone-shaped. In scatter plots, variance increases with the increase in fitted value. For cross-sectional studies like income, the range is from poverty to high-income citizens; when plotted on a graph, the data is heteroskedastic.

Heteroskedasticity is categorized into two types.

1. Pure heteroskedasticity
2. Impure heteroskedasticity

In pure heteroskedastic dispersion, the chosen statistical model is correct. But with, impure (residual) heteroskedastic dispersion errors are observed—as a result, the statistic model is incorrect for the given data. These errors cause variance.

There are three methods to fix heteroskedasticity and improve the model -

1. Redefining variables
2. Weighted regression
3. Transform the dependent variable

In the first method, the analyst can redefine the variables to improve the model and get desired results with accuracy. In the second method, the regression analysis is appropriately weighted. Finally, the third approach is to interchange the working in every model. For example, there is a dependent variable and a predictor variable; by changing the dependent variable, the whole model gets revamped. Thus, it is an important approach to move forward.

Independent variables used in regression analyses are referred to as the predictor variable. The predictor variable provides information on an associated dependent variable regarding a particular outcome.

It is imperative to determine whether data exhibits pure heteroskedastic dispersion or impure heteroskedastic dispersion—the approach varies for each subtype. Furthermore, improving the variables used in the impure form is important. If ignored, these variables cause bias in coefficient accuracy, and p-values become smaller than they should be.

Heteroskedastic dispersion is caused due to the following reasons.

• It occurs in data sets with large ranges and oscillates between the largest and smallest values.
• It occurs due to a change in factor proportionality.
• Among other reasons, the nature of the variable can be a major cause.
• It majorly occurs in cross-sectional studies.
• Some regression models are prone to heteroskedastic dispersion.
• An improper selection of regression models can cause it.
• It can also be caused by data set formations and inefficiency of calculations as well.

Example #1

The most basic heteroskedastic example is household consumption. The variance in consumption increases with an increase in income—directly proportional. Because when the income is low, the variance in consumption is also low. Low-income people spend predominantly on necessary items and bills—less variance. In contrast, with the increase in income, people tend to buy luxurious items and develop a plethora of habits—less predictable.

Example #2

A coach correlating runs scored by each player with time spent in training is an example of homoskedasticity. In this case, the scores would become the dependent variable, and training time is the predictor variable.

Example #3

The basic application of heteroskedasticity is in the stock market—variance in stock is compared for different dates. In addition, investors use heteroskedastic dispersion in regression models to track securities and portfolios. Heteroskedastic dispersion can or cannot be predicted depending on the particular situation taken into a study.

For example, when the prices of a product are studied at the launch of a new model, heteroskedasticity is predictable. But for rainfall or income comparisons, the nature of dispersion cannot be predicted.

• Homokedasticity refers to equal variance in residuals. Unequal variance in residuals, on the other hand, cause heteroskedastic dispersion. In regression analysis, the term ‘residual’ refers to the difference between observed and predicted data.
• When using regression models, researchers look for Homoskedastic dispersion. Heteroskedastic dispersion, therefore, is seen as a problem to be solved.
• Homoskedasticity is rare, whereas heteroskedastic dispersion is commonly observed in real-world examples. 
• Homoskedasticity is also referred to as homogeneity of variance. On the other hand, heteroskedasticity is often called an ‘error.’
• Homoskedasticity is not categorized, but heteroskedastic dispersion has subtypes—pure and impure.

This is a guide to Heteroskedasticity & its definition. We explain it in regression with examples and compare it with homoskedasticity. You can learn more about it from the following articles -

• Best Econometrics Books
• Inferential Statistics
• Descriptive Statistics