Table Of Contents
Frequently Asked Questions (FAQs)
What does dispersion mean in statistics?
What causes dispersion?
What are the three measures of dispersion?
Dispersion Meaning
In statistics, dispersion (or spread) is a means of describing the extent of distribution of data around a central value or point. It aids in understanding data distribution. Lower dispersion indicates higher precision in the manufacturing process or data measurements, whereas higher dispersion means lower accuracy.
One can use dispersion to understand the variation in the values of the data set. It helps to assess the data quality in a quantifiable manner. In finance, it enables investors to determine the statistical distribution of probable returns on their investments. Range, variance, mean deviation, and standard deviation are some of the common measures of dispersion.
Key Takeaways
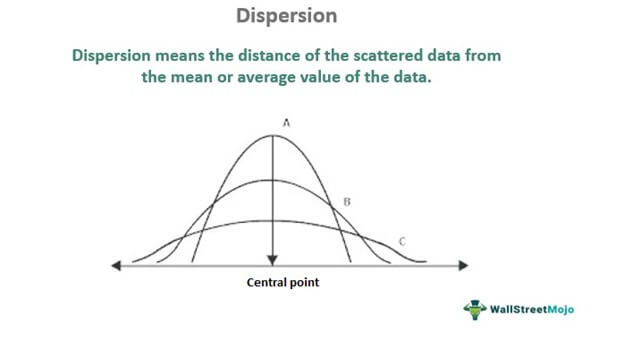
- Dispersion means the distance of the scattered data from the central value of the data.
- It gives information regarding the volatility or non-volatility nature of the data set. More distance from the central point represents a more volatile nature and vice versa.
- In finance, dispersion is inversely proportional to securities' efficiency, yield, or performance.
- Measure of dispersion can be absolute or relative. Absolute measures have the same unit of measurement as the given dataset, while relative measures are expressed as ratios and percentages.
Dispersion in Statistics Explained
Dispersion (scatter or variation) can have multiple meanings based on the context it is used in. For instance, in statistics, it is the factor that helps determine the extent of variation of values in a particular data set.
At the same time, it allows investors to estimate the statistical distribution of potential portfolio returns in finance. Thus, spread is the measurement of the variability of an item from other items in a data set and from its central value.
Usually, using the measure of central tendency to describe a certain set of data is not enough. The measure of central tendency can help know the mean, median, or mode of data sets, but the measure of the variation can only be known through dispersion. Hence, the analysis of data using statistics is done by:
- Measure of central tendency
- Measure of dispersion (MOD)
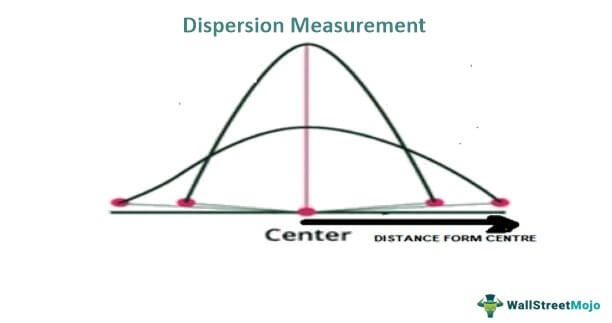
Measuring spread gives us accurate information on vertical data distribution statistics as per the histogram. However, the information obtained from it is more related to the separation of data points, the difference in the values of the data set, and the distance of every single data point from the mean value of the entire data set.
In other words, it shows how data are spread and how different they are from one another, i.e., the homogeneity or heterogeneity of data in a distribution. If the distance between a data point and its mean value is:
- More, then the data set is said to be volatile
- Less, then the data is said to be less volatile, safer, or high yielding
Measures of Dispersion in Statistics
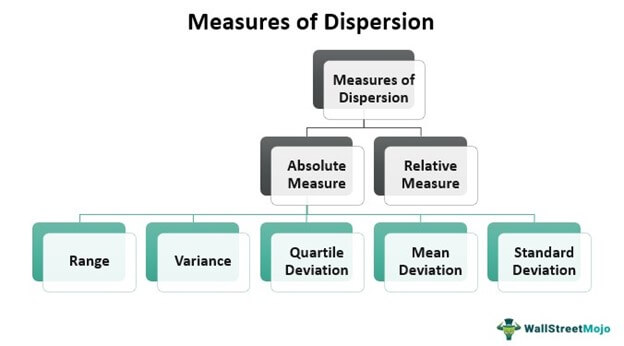
There are two methods to measure the degree of variation present in the data set:
- Absolute Measure
- Relative Measure
#1 - Absolute Measure
It refers to the average of deviations of data like standard deviation or mean deviation. It has the same unit assigned to the original data set like centimeters, meters, kilograms, etc. Here are some absolute measures of spread.
- Range (R)
Range refers to the difference between the largest and the smallest values in a given data set. The higher the value of the range, the higher the spread in data.
R = L - D
where,
L = Largest value
S = Smallest value
- Quartile deviation (QD)
A quartile distributes a data set in four equal valued sets. Each data set has the smallest number, the largest number, and the median. Q2 or second quartile is the median of the data. The first quartile (Q1) connects the smallest number with Q2, while the third quartile (Q3) joins the largest number with Q2.
The interquartile range is the difference between the third quartile and the first quartile. Half of the interquartile range is the quartile deviation.
Hence, Interquartile range (IR) = Q3 – Q1
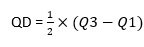
- Mean deviation (MD)
Mean deviation measures the deviation of data from its central point (mean, median, or mode). It is the arithmetic mean of the absolute deviations of the data from the central value.
Mean deviation = Total of all absolute deviations value/ Total number of observations
- Variance
It is the average of the sum of the square of the difference between each data point from the mean. The higher the variance, the higher the scattering of data from the mean and vice-versa.
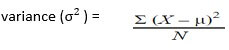
Σ = sum of, Χ = each value, μ = mean, Ν = number of values in the dataset
- Standard Deviation (SD)
It is the most widely used method for measuring spread. Mathematically, it is the square root of the variance.

where,
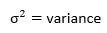
#2 - Relative Measure
The relative measure is a type of dispersion expressed in ratios and percentages. Since it is independent of original units, it is used for comparative analysis of two or more data set distributions with different units of measurement. Also, relative measures are used to compare datasets that have varying averages.
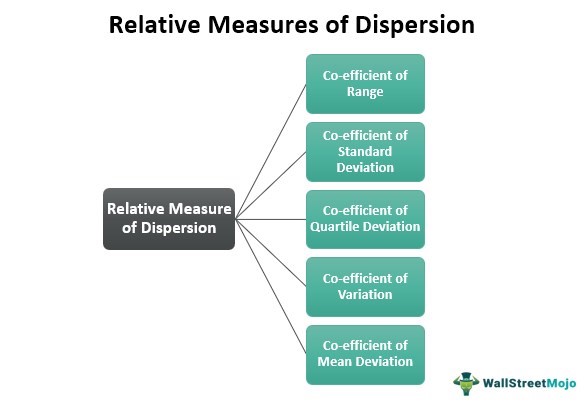
- Co-efficient of Range (COR)
It is the ratio of the difference between the largest and smallest values in a distribution to the sum of the largest and smallest values in a distribution.
COR = L-S/L+S
where,
L= largest value
S = Smallest value
- Coefficient of Variation (COV)
It is used to contrast two data sets based on their consistency.
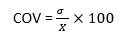
where,
X = Mean
σ = standard deviation
- Co-efficient of Standard Deviation (COS)
It is the standard deviation divided by the mean of the data set.
COS = SD/Mean
where,
SD is the standard deviation
- Co-efficient of Quartile Deviation (COQ)
It is the ratio of the difference between the third and the first quartile to the sum of the third and the first quartile of the data set.
COQ = Q3 – Q1/ Q3 + Q1
- Co-efficient of Mean Deviation (COM):
It is calculated using either the mean, median, or mode of the data.
COM = MD/Mean
Or
COM = MD/Median
Or
COM = MD/Mode
where,
MD = Mean deviation
Examples
Let us go through the following dispersion examples for a better understanding of the concept.
Example #1
Let us take an example from the stock market domain. A certain security A is being traded on the exchange. The traders who want to invest in security A will look at its historical return data for the last year. They will assess the extent of scattering of the security’s return over the past year.
If the degree of scattering of returns is less, it means less price fluctuation. Thus, the security will be considered a safer investment with low risk. Moreover, if the degree of spread of security A is higher, it means the price is highly volatile. Therefore, the security will be taken as an unsafe investment in such a case.
In other words, higher dispersion means riskier investment and vice versa.
Example #2
Let’s consider two varieties of coffee – X & Y with different yields.
Coffee X and Y have the following yields for a period of six months:
| Coffee Variety | January | February | March | April | May | June |
|---|---|---|---|---|---|---|
| X | 36 | 31 | 32 | 34 | 30 | 33 |
| Y | 58 | 42 | 33 | 29 | 50 | 20 |
To know the spread of each variety of coffee, let’s calculate its range.
Range (R) = Largest value (L) – Smallest Value (S)
| Coffee Variety | Largest value (L) | Smallest Value (S) | Range (R = L - S) |
|---|---|---|---|
| X | 36 | 30 | 6 |
| Y | 58 | 20 | 38 |
As mentioned before, the higher the range, the greater the data spread. Thus,
- X has a lower range. It means it has less scattered data or a more homogeneous data set.
- Y has a higher range. It represents a highly scattered data set or a more heterogeneous data set.
Therefore, X has a lower spread than Y. Lower spread means better yield, and a higher spread represents lower yield. Hence, higher dispersion in data means lesser returns, and lower dispersion in the data set means higher returns.
