Swaps in Finance

What are Swaps in Finance?

Swaps in finance involve a contract between two or more parties on a derivative contract which involves an exchange of cash flow based on a predetermined notional principal amount, which usually includes interest rate swaps which is the exchange of floating rate interest with a fixed rate of interest and the currency swaps which is the exchange of fixed currency rate of one country with floating currency rate of another country etc.

Under the Swaps agreement, one party exchanges fixed cash flows in return for floating cash flows exchanged by the other counterparty. The most common kind of swaps in finance is Interest rates and Currency Swaps.

• "Swaps" refer to derivative contracts where two or more parties exchange cash flows based on a predetermined principal amount.
• This category encompasses interest rate swaps, involving replacing a floating interest rate with a fixed rate, and currency swaps, replacing a fixed currency rate from one country with a floating rate from another.
• The financial industry offers diverse swap types, covering commodities, currencies, volatility, debt, puttable swaptions, credit default, and more. Swaps serve as versatile tools for risk management and financial optimization.

Swaps In Finance Explained

Swaps in finance are an OTC derivative contract between two parties exchanging a sequence of cash flows with another at a predetermined rate for a set period. A plain vanilla interest rate swap exchanges fixed-rate payment for floating-rate payment throughout swaps. A swap contract is equivalent to a simultaneous position in two bonds. The comparative rate advantage suggests that when one of the two borrowers has a comparative advantage in either the fixed or floating rate market, the better their liability by entering into the Swap.

The value of the Swap for a fixed-rate receiver is the difference between the present value of the remaining fixed-rate payment and the present value of the remaining floating-rate payment. For a floating rate, the receiver is the difference between the present value of the remaining floating-rate payment and the present value of the remaining fixed-rate payment.

Currency swaps exchange cash flows in different currencies along with the principal amount at inception and maturity, though not obligatory.

Types

There are several types of Swaps transacted in the financial world. They are commodity, currency, volatility, debt, credit default, puttable, swaptions, Interest rate swap, equity swap, etc.

Like an Interest rate swap (as explained above), Currency Swaps (also known as Cross Currency Swaps) are derivative contracts to exchange certain cash flows at a predetermined time. The basic difference here is that under currency swaps, the principal is exchanged (not obligatory) at the inception and maturity of the contract, and cash flows are in different currencies, generating a larger credit exposure.

Another difference between these types of swaps is that in Interest Rate swaps, cash flows are netted at the time of settlement, whereas, in the currency swap, the same is not netted but exchanged between parties.

Valuation

As we know, a Swap is nothing but a series or a combination of bonds for both counterparties, so its valuation is also easy.

For example, suppose that two counterparties, A and B, enter into a Swaps agreement wherein A pays fixed and receives a float (refer to image: 2 below). In this arrangement, if we see, there is a package of two bonds for A.

1. A is short on fixed coupon paying bond and
2. Long on floating coupon paying a bond.

At any given point in time, the value of the Swap for a fixed ratepayer is the difference between the present value of the remaining floating-rate payment and the present value of the remaining fixed-rate payment (B_float – B_fixed). Whereas for a fixed-rate receiver, the value of the Swap is the difference between the present value of the remaining fixed-rate payment and the present value of the remaining floating-rate payment (B_fixed – B_float). We can calculate the value of a Swap for either party and then find out for another easily as a swap is a derivative contract. We know that a derivative is a zero-sum game wherein profit for one party is equal to the loss of another. Hence, the formula for the value of the swap agreement can be summarized below:

• Value of a Swap agreement (for a Floating ratepayer) = PV of remaining fixed-rate payment (B_fixed) – Value of remaining floating-rate payment (B_float) or B_{fixed –} B
• Value of a Swap agreement (for a Fixed ratepayer) = PV of remaining float rate payment (B_float) – Value of remaining fixed-rate payment (B_fixed) or B_{float –} B

Here, one point is to be noted that at the date of settlement, the value of the floating coupon bond is always equal to the notional principal as at the date of settlement coupon rate is equal to YTM, or the bond is par bond.

Valuation of Swaps - Before the date of settlement

Let’s see how valuation is done if the contract is not terminated on the settlement date.

As explained above, the valuation for fixed leg payment shall remain the same. But the valuation for the floating leg is slightly changed. Here, since we are not standing on the settlement date, the floating-rate payment discounting shall be a Notional Principal + Floating rate payment for the remaining period.

Let’s look at the example.

Suppose A & B enters into a Swap Agreement for two years wherein A pays fixed (here A is short on a fixed coupon paying bond) at the rate of 4% and receives LIBOR from B. After one and a half years, both parties want to terminate the agreement immediately.

A notional principal is Rs.1,00,000/- and two years LIBOR is 4.5%.

Value of Swaps = B_{float -} B_{fixed, Where,}

B_float = PV of all remaining float rate payment and,
B_fixed = PV of remaining fixed-rate payment.

B_float= since valuation is happening six months before the settlement, the PV of floating-rate payment would be the notional principal, i.e., Rs.100000/- plus the floating rate coupon payment, which is due in the next six months. The same can be found using two years of LIBOR curve.

(P+C)*e^-r*t = (100000 + 4500)* e^-0.045*0.5

= 102175.00

Hence, B_float = Rs.102175.00

_{B fixed = Total fixed payment to be made by A for the second year is principal of Rs.100000/- and interest of Rs.4000/- (100000*0.04). This amount needs to be discounted with two years LIBOR, i.e., 4.5% for six months, as six months are left to expire the contract.}

(P+C)*e^-r*t = (100000+4000)*e^-0.045*0.5

= 101686.12

Hence, B_fixed = 101686.12

Value of Swaps = Rs.102175 – Rs.101686.12

= Rs.488.88

Valuation of Currency Swaps in Finance

Currency swaps are valued similarly to interest rate swaps, using DCF (bond method). Hence,

Value of Currency Swaps (long on one bond) = B_{long on a currency -} S_o*B_{short on currency,}

Value of Currency Swaps (short on one bond) = B_{short on a currency -} S_o*B_{long on currency, where}

S_{0 =} Spot rate of the currency

Let’s understand this through a numerical.

Considering the above example, assume that the interest rate in India is 6%, and in the USA, it is 4%. Assume that the interest rate remains constant throughout the life of the Swaps agreement in both the economy. Exchange rates for the currencies are INR 65/USD.

Before proceeding to value the swap contract, first look at the cash flows in the below table:

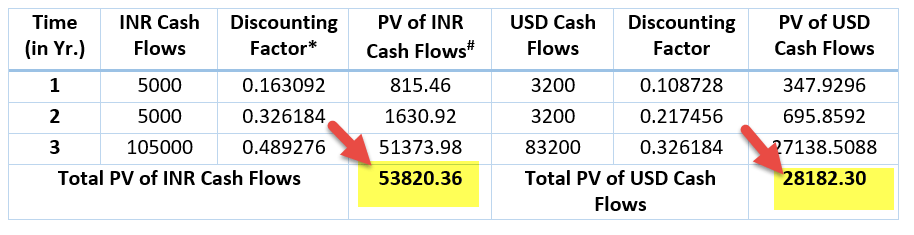
* Discounting factor has arrived through formula e^-r*t

# PV of Cash flows have arrived through the formula Cash Flows*Discounting Factor

As mentioned above, the valuation of currency swaps is also done through discounted cash flow. Therefore, here we will calculate the total PV of Cash flows in both currencies.

PV of INR Cash Flows = INR 53820.36

PV of USD Cash Flows = USD 28182.30

Since EDU Inc. is long on USD and short on INR, therefore,

Value of Swaps = B_USD - S₀*B_INR

= 28182.30 – (1/65)*53820.36

= 28182.30 – 828.01 = 27354.49

Examples

Let us understand it with the help of an example.

Example 1

EDU Inc. enters into a financial contract with CBA Inc. in which they have agreed to exchange cash flows making LIBOR as its benchmark wherein EDU Inc. will pay a fixed rate of 5% and receive a floating rate of LIBOR+2% from CBA Inc.

Now, we see that both parties have two legs to the transaction in this financial contract.

• EDU Inc. is paying the fixed rate of 5% and receiving a floating rate (Annual LIBOR+2%), whereas CBA Inc. is producing a floating rate (Annual LIBOR+2%) and receiving a fixed percentage (5%).

In order to understand this, let’s look into the numerical now.

In the above example, let's assume that both parties have entered into a swaps contract for one year with a notional principal of Rs.1,00,000/-(since this is an Interest rate swap, the principal will not be exchanged). And after one year, the one-year LIBOR in the prevailing market is 2.75%.

We will analyze the cash flows for two scenarios:

1. When the one year LIBOR is 2.75%,
2. When the one year LIBOR increased by 50 bps to 3.25%

Scenario 1 (When one year LIBOR is 2.75%)

Scenario 2 (When one year LIBOR is 3.25%)

Looking at the above exchange of cash flows, an obvious question comes to our mind: why do financial institutions enter into swap agreements. It is seen in scenario one that a fixed-paying party benefited from the swaps. However, when the one-year LIBOR increased by 50 bps to 5.25%, it was in loss from the same swap agreement.

The answer to this is a comparative rate advantage to both parties.

Example 2

Suppose A & B enters into a Swap Agreement for two years wherein A pays fixed (here A is short on a fixed coupon paying bond) at the rate of 4% and receives LIBOR from B. One year has already crossed, and both parties want to terminate the agreement immediately.

A notional principal is Rs.1,00,000/- and two years LIBOR is 4.5%.

Scenario -1 (if party A pays fixed)

Here, since the swap agreement was supposed to end after two years, it is being terminated by the counterparties only after one year. Hence, we must value the Swap at the end of one year.

As per the above formula, a value of Swap = B_{float – B fixed, Where,}

Afloat = PV of all remaining float rate payment and,
B_fixed = PV of remaining fixed-rate payment.

Calculations:

B_float= since we are valuing the Swap at the settlement date, the PV of floating-rate payment would be the notional principal, i.e., Rs.100000/-. Also, it is assumed that coupon payment has been made to a long party on the date of settlement.Hence, B_float = Rs.100000/-

B _fixed = The total fixed payment to be made by A for the second year is principal of Rs.100000/- and interest of Rs.4000/- (100000*0.04). This amount needs to be discounted with two years LIBOR, i.e., 4.5%.

(P+C)*e^-r*t = (100000+4000)*e^-0.045*1

= 99423.74

Hence, B_fixed = 99423.74

Value of Swaps = Rs.100000 – Rs.99423.74

= Rs.576.26

Scenario -2 (if party A pays float)

As per the above formula, the value of Swap = B_{fixed -} B_float,

Calculations:

B_float= Here also, the PV of floating-rate payment would be the notional principal, i.e., Rs.100000/- as we are valuing the Swap at the settlement date.

Hence, B_float = Rs.100000/-.

_{B fixed = The total fixed payment to be made by B for the second year is principal of Rs.100000/- and interest of Rs.4000/- (100000*0.04). We will discount this amount with two years LIBOR, i.e., 4.5%.}

(P+C)*e^-r*t = (100000+4000)*e^-0.045*1

= 99423.74

Hence, B_fixed = 99423.74

Value of Swaps = Rs.99423.74 - Rs.100000

= - Rs.576.26

In the above-explained scenarios, we have seen Swaps' valuation on the settlement date. But what if the contract is not terminated on the date of settlement?

Example 3

This example explains the mechanics of currency swaps.

Suppose two companies EDU Inc. (based in the US) and CBA Inc. (based in India), entered into currency swaps, wherein EDU Inc. pays 5% in INR and receives 4% in USD (and CBA Inc. pays 4% in USD and receives 5% in INR) every year for the next two years (refer Image: 3). At the beginning of the contract, both the parties exchanged a certain amount of principal (EDU Inc. exchanged USD 80000, and CBA Inc. exchanged INR 100000). The current spot rate is INR 65/USD.

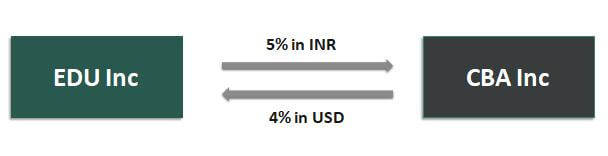
Here, at each settlement date, EDU Inc. shall pay INR 5000 (100000*0.05) to CBA Inc. and receive USD 3200 (80000*0.04) from CBA Inc. Further, at the end of the contract, both the parties shall exchange the principal amount, i.e., EDU Inc. shall pay INR 100000, and CBA Inc. shall pay USD 80000.

Comparative Rate Advantage

The comparative rate advantage suggests that when one of the two borrowers has a comparative advantage in either the fixed or floating rate market, the better their liability by entering into swaps. It reduces the cost for both parties. However, a comparative advantage argument assumes that no credit risk is involved, and funds can be borrowed during the Swap's life.

To understand the comparative rate advantage, let’s assume that EDU Inc. and CBA Inc. have borrowing capacities in both a fixed and a floating market (as mentioned in the table below).

Company	Fixed Market Borrowing	Floating Market Borrowing
EDU Inc.	4.00%	One year LIBOR-0.1%
CBA Inc.	5.20%	One year LIBOR+0.6%

The above table shows that EDU Inc. has an absolute advantage in both markets, whereas CBA Inc. has a comparative advantage in the floating rate market (as CBA Inc. is paying 0.5% more than EDU Inc.). Assuming both parties have entered into a Swap agreement with the condition that EDU Inc. will pay one year LIBOR and receive 4.35% p.a.

The cash flows for this agreement are described in the table below for both parties.

Cash Flows for EDU Inc.
Receivable in a Swap agreement	4.35%
Payable in a Swap agreement	LIBOR
Payable in fixed market borrowing	4.00%
Net Effect	LIBOR-0.35%
Cash Flows for EDU Inc.
Receivable in the Swap agreement	LIBOR
Payable in the Swap agreement	4.35%
Payable in floating market borrowing	LIBOR+0.6%
Net Effect	4.95%

Looking at the above cash flows, we can say that EDU Inc. has a net cash flow of LIBOR – 0.35% per annum, giving it an advantage of 0.25%, which EDU Inc. had to pay if it went directly into the floating market, i.e., LIBOR – 0.1%.

In the second scenario for CBA Inc., the net cash flow is 4.95% per annum, giving it an advantage of 0.25% in the fixed borrowing market if it had gone directly, i.e., 5.20%.

Frequently Asked Questions (FAQs)

Recommended Articles

This has been a guide to what are Swaps in Finance. Here, we explain the concept with types, valuation, examples, and competitive rate advantage. You may also have a look at the following articles –

• Embedded Derivatives
• Top Derivatives Books
• Options in Finance
• Option Trading Strategies