Convexity of a Bond

Convexity of a Bond is a measure that shows the relationship between bond price and Bond yield, i.e., the change in the duration of the bond due to a change in the rate of interest, which helps a risk management tool to measure and manage the portfolio’s exposure to interest rate risk and risk of loss of expectation.

As we know, the bond price and the yield are inversely related, i.e., as yield increases, the price decreases. However, this relation is not a straight line but is a convex curve. Convexity measures the curvature in this relationship, i.e., how the duration changes with a change in yield of the bond.

The duration of a bond is the linear relationship between the bond price and interest rates, where, as interest rates increase, bond price decreases. Simply put, a higher duration implies that the bond price is more sensitive to rate changes. For a small and sudden change in bond, yield duration is a good measure of the sensitivity of the bond price. However, for larger changes in yield, the duration measure is not effective as the relationship is non-linear and is a curve. There are four different types of Duration measures, namely Macaulay’s Duration, Modified Duration, Effective duration, and Key rate duration, which all measure how long it takes for the price of the bond to be paid off by the internal cash flows. What they differ is in how they treat the interest rate changes, embedded bond options, and bond redemption options. They, however, do not take into account the non-linear relationship between price and yield.

Convexity measures the sensitivity of the bond’s duration to change its yield. Convexity is a good measure for bond price changes with greater fluctuations in the interest rates. Mathematically speaking, convexity is the second derivative of the formula for change in bond prices with a change in interest rates and a first derivative of the duration equation.

For a Bond of Face Value USD1,000 with a semi-annual coupon of 8.0% and a yield of 10% and 6 years to maturity and a present price of 911.37, the duration is 4.82 years, the modified duration is 4.59, and the calculation for Convexity would be:

Annual Convexity : Semi-Annual Convexity/ 4=  26.2643Semi Annual Convexity :  105.0573

In the above example, a convexity of 26.2643 can be used to predict the price change for a 1% change in yield would be:

If the only modified duration is used:

Change in price =   - Modified Duration *Change in yield

Change in price for 1% increase in yield = ( - 4.59*1%) =  -4.59%  

So the price would decrease by 41.83

To accommodate the convex shape of the graph, the change in price formula changes to:

Change in price = +

Change in price for 1% increase in yield = + = -4.46%  

So the price would decrease by only 40.64 instead of 41.83

This shows how, for the same 1% increase in yield, the predicted price decrease changes if the only duration is used as against when the convexity of the price yield curve is also adjusted.

So the price at a 1% increase in yield as predicted by Modified duration is 869.54 and as predicted using modified duration and convexity of the bond is 870.74. This difference of 1.12 in the price change is due to the fact that the price yield curve is not linear as assumed by the duration formula.

As seen in the convexity calculation can be quite tedious and long, especially if the bond is long term and has numerous cash flows. The formula for convexity approximation is as follows:

As can be seen from the formula, Convexity is a function of the bond price, YTM (Yield to maturity), Time to maturity, and the sum of the cash flows. The number of coupon flows (cash flows) change the duration and hence the convexity of the bond. The duration of a zero bond is equal to its time to maturity, but as there still exists a convex relationship between its price and yield, zero-coupon bonds have the highest convexity and its prices most sensitive to changes in yield.

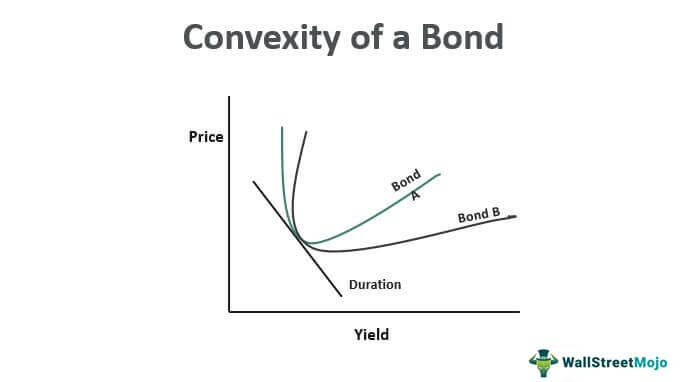
In the above graph, Bond A is more convex than Bond B even though they both have the same duration, and hence Bond A is less affected by interest rate changes.

In the above graph, Bond A is more convex than Bond B even though they both have the same duration, and hence Bond A is less affected by interest rate changes.

Convexity is a risk management tool used to define how risky a bond is as more the convexity of the bond; more is its price sensitivity to interest rate movements. A bond with a higher convexity has a larger price change when the interest rate drops than a bond with lower convexity. Hence when two similar bonds are evaluated for investment with similar yield and duration, the one with higher convexity is preferred in stable or falling interest rate scenarios as price change is larger. In a falling interest rate scenario again, a higher convexity would be better as the price loss for an increase in interest rates would be smaller.

Convexity can be positive or negative. A bond has positive convexity if the yield and the duration of the bond increase or decrease together, i.e., they have a positive correlation. The yield curve for this typically moves upward. This type is for a bond that does not have a call option or a prepayment option. Bonds have negative convexity when the yield increases, the duration decreases, i.e., there is a negative correlation between yield and duration, and the yield curve moves downward. These are typically bonds with call options, mortgage-backed securities, and those bonds which have a repayment option. If the bond with prepayment or call option has a premium to be paid for the early exit, then the convexity may turn positive.

The coupon payments and the periodicity of the payments of the bond contribute to the convexity of the bond. If there are more periodic coupon payments over the life of the bond, then the convexity is higher, making it more immune to interest rate risks as the periodic payments help in negating the effect of the change in the market interest rates. If there is a lump sum payment, then the convexity is the least, making it a more risky investment.

For a bond portfolio, the convexity would measure the risk of all the bonds put together and is the weighted average of the individual bonds with no bonds or the market value of the bonds being used as weights.

Even though Convexity takes into account the non-linear shape of the price-yield curve and adjusts for the prediction for price change, there is still some error left as it is only the second derivative of the price-yield equation. To get a more accurate price for a change in yield, adding the next derivative would give a price much closer to the actual price of the bond. Today with sophisticated computer models predicting prices, convexity is more a measure of the risk of the bond or the bond portfolio. More convex the bond or the bond portfolio less risky; it is as the price change for a reduction in interest rates is less. So bonds, which are more convex, would have a lower yield as the market prices are lower risk.

Risk measurement for a bond involves a number of risks. These include but are not limited to:

1. Market risk that changes in the market interest rate in an unprofitable manner
2. Prepayment risk that is the bond is repaid earlier than the maturity date hence disrupting the cash flows
3. Default risk that is the bond issuer would not pay the interest or the principal amount.

The interest rate risk is a universal risk for all bondholders as all increase in interest rate would reduce the prices, and all decrease in interest rate would increase the price of the bond. This interest rate risk is measured by modified duration and is further refined by convexity. Convexity is a measure of systemic risk as it measures the effect of change in the bond portfolio value with a larger change in the market interest rate while modified duration is enough to predict smaller changes in interest rates.

As mentioned earlier, convexity is positive for regular bonds, but for bonds with options like callable bonds, mortgage-backed securities (which have prepayment option), the bonds have negative convexity at lower interest rates as the prepayment risk increases. For such bonds with negative convexity, prices do not increase significantly with a decrease in interest rates as cash flows change due to prepayment and early calls.

As the cash flow is more spread out, the convexity increases as the interest rate risk increases with more gaps in between the cash flows. So convexity as a measure is more useful if the coupons are more spread out and are of lesser value. If we have a zero-coupon bond and a portfolio of zero-coupon bonds, the convexity is as follows:

1. The duration of the zero-coupon bond which is equal to its maturity (as there is only one cash flow) and hence its convexity is very high
2. While the duration of the zero-coupon bond portfolio can be adjusted as to that of a single zero-coupon bond by varying the nominal and maturity value of the zero-coupon bonds within the portfolio. However, the convexity of this portfolio is higher than the single zero-coupon bond. This is because the cash flows of the bonds in the portfolio are more dispersed than that of a single zero-coupon bond.

Convexity of bonds with a put option is positive, while that of a bond with a call option is negative. This is because when a put option is in the money, then if the market goes down, you can put the bond, or if the market goes up, you preserve all the cash flows. This makes the convexity positive. However, for a bond with a call option, the issuer would call the bond if the market interest rate decreases, and if the market rate increases, the cash flow would be preserved. Due to the possible change in cash flows, the convexity of the bond is negative as interest rates decrease.

The measured convexity of the bond when there is no expected change in future cash flows called modified convexity. When there are changes expected in the future cash flows, the convexity that is measured is the effective convexity.

Convexity arises due to the shape of the price-yield curve. If the market yield graph were flat and all shifts in prices were parallel shifts, then the more convex the portfolio, the better it would perform, and there would be no place for arbitrage. However, as the yield graph is curved, for long-term bonds, the price yield curve is hump-shaped to accommodate for the lower convexity in the latter term.

Finally, convexity is a measure of the bond or the portfolio’s interest-rate sensitivity and should be used to evaluate investment based on the risk profile of the investor.

• Maturity Value
• ABS and MBS Index
• Bond Pricing
• Accounting for Convertible Bonds