Duration

Duration is a risk measure used by market participants to measure the interest rate sensitivity of a debt instrument, e.g., a Bond. It tells how sensitive a bond is with respect to the change in interest rates. This measure can be used for comparing the sensitivities of bonds with different maturities. There are three different ways to arrive at duration measures, viz. Macaulay Duration, Modified Duration, and Effective Duration.

Bond duration is vastly affected by factors such as coupon rate and time to maturity. However, the fundamental idea is that the bond’s value decreases with an increase in its duration. As the time frame rises, the bond’s price will experience a decrease and the interest rates might be higher.

• Duration measures a bond's price sensitivity to changes in interest rates.
• Duration represents the weighted average time it takes to receive the bond's cash flows, including coupon payments and the return of principal.
• Investors and portfolio managers widely use duration to manage interest rate risk. By understanding the duration of their bond holdings, investors can make informed decisions about the impact of interest rate changes on their portfolio
• Duration and interest rates have an inverse relationship. As interest rates rise, the duration of a bond decreases, indicating that its price will be more sensitive to interest rate changes. Conversely, as interest rates decline, the duration increases, indicating reduced price sensitivity.
  

Duration is a measurement of the sensitivity of a debt instrument such as bonds and other debt instrument with relation to interest rates. The interest rates changes are majorly reliant on the time to maturity and coupon rate of the bond.

As the time frame of maturity rises, the base value of the bond experiences and dip and the interest rates are most likely to rise.

As bond price is inversely proportional to yield, it is highly sensitive to how yield changes. The duration measures defined above quantify the impact of this sensitivity on bond price.

A bond with a longer maturity will have a longer duration; hence, it is more sensitive to changes in interest rates.

A bond with a lower coupon rate will be more sensitive than a bond with a bigger coupon. However, the reinvestment risk will be higher in the case of a small coupon bond.

Effective duration calculator is an approximate measure of duration, and for an option-free bond, the modified and effective duration will be almost the same. Modified duration quantifies the sensitivity by specifying the percentage change in bond price for every 100-bps change in the interest rates.

There are three different types to calculate duration measures.

Each of these types of formula has its intricacies and can be used to calculate the bond duration and that of other debt securities. Let us understand each of the formulas through the discussion below.

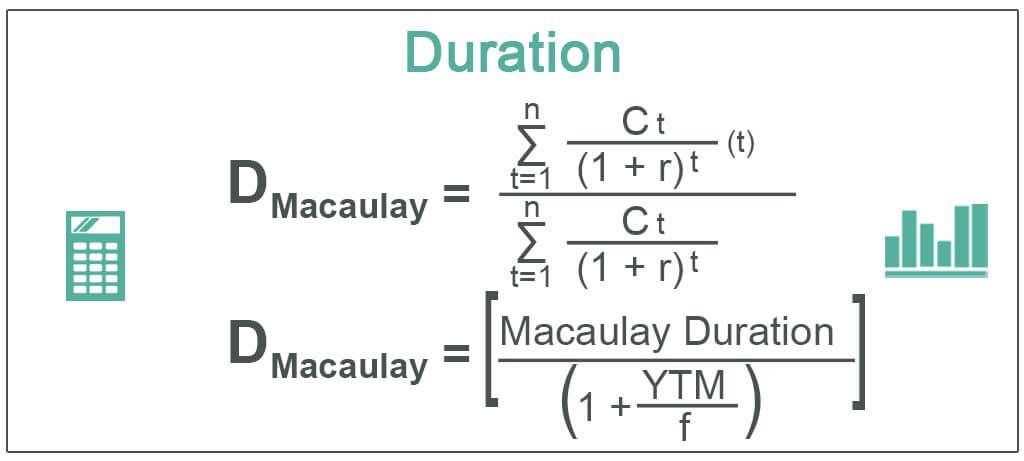
#1 - Macaulay Duration

The Mathematical Definition: “Macaulay Duration of a coupon-bearing bond is the weighted average time period over which the cash flows associated with the bond are received.”  In simple terms, it tells how long it will take to realize the money spent to buy the bond in the form of periodic coupon payments and the final principal repayment.

where:

• Ct: Cashflow at time t
• r: Interest rates/ Yield to maturity
• N: Residual Tenure in Years
• t: Time/ Period in Years
• D: Macaulay Duration

#2 - Modified Duration

The Mathematical Definition: "Modified Duration is the percentage change in Price of a Bond for a unit change in yield." It measures the price sensitivity of a bond to changing interest rates. The interest rates are picked from the market yield curve, adjusted for the riskiness of the bond and the appropriate tenure.

Modified Duration = Macaulay Duration / (1+ YTM/f)

Where:

• YTM: Yield to Maturity
• f: Coupon frequency

#3 - Effective Duration

If a bond has some options attached to it, i.e., the bond is puttable or callable before maturity. Effective duration takes into consideration the fact that as interest rate changes, the embedded options may be exercised by the bond issuer or the investor, thereby changing the cash flows and hence the duration.

D_effective = -

Where:

• P_up: Bond price with yield up by Δi
• P_down: Bond price with yield down by Δi
• P: Bond price at current yield
• Δi: Change in yield (usually taken as 100 bps)

Let us understand the duration calculator with the help of an examples. This detailed calculation will help us understand the intricate details about the concept and how investors can calculate the duration of their debt instruments.

Consider a bond with the face value of 100, paying a semi-annual coupon of 7% PA compounded annually, issued on 1 Jan 19 and with a tenure of 5 years and trading at par, i.e., the price is 100 and yield is 7%.

Calculation of three types of duration is as follows -

Please download the above Excel template for detailed calculation.

Although highly used as a duration calculator and one of the prominent risk measures for fixed-income securities, the duration is restricted for wider use because of underlying assumptions of interest rates movement. It assumes:

• Market yield will be the same for the entire tenure of the bond
• There will be a parallel shift in market yield, i.e., Interest rate changes by the same amount for all the maturities.

Both limitations are handled by considering regime-switching models, which provide for the fact that there can be different yields and volatility for different periods, thereby ruling out the first assumption. And by dividing the tenure of bonds into certain key periods basis, the availability of rates or basis the majority of cash flows lying around certain periods. This helps in accommodating non-parallel yield changes, hence taking care of the second assumption.

Let us understand the advantages of using bond duration calculators and for other debt instruments. These pointers will give us a deeper understanding of the concept.

• A bond with longer maturity is more sensitive to changes in interest rates. This understanding can be utilized by a bond investor to decide whether to stay invested in or sell off the holding. e.g., If Interest rates are expected to go low, an investor should plan to stay long in long-term bonds. And if interest rates are expected to go high, short-term bonds should be preferred.
• These decisions become easier with the use of Macaulay duration as it helps in comparing the sensitivity of bonds with different maturities and coupon rates. Modified duration gives one level deeper analysis of a particular bond by giving the exact percentage by which the prices can change for a unit change in yield.
• It measures one of the key risk measures along with DV01 PV01s. Thereby, monitoring of portfolio duration becomes all the more important in deciding what kind of portfolio will better suit the investment needs of any financial institution.

Despite various advantages, there are a few factors that prove to be hassle or pain points for investors. Let us understand the disadvantages of using a duration calculator through the explanation below.

• Duration being a one-factor risk metric can go awry in highly volatile markets, in troubled economies. It also assumes a linear relationship between the price of the bond and interest rates. However, the price – interest rate relation is convex. Hence, this measure alone is not sufficient to estimate sensitivity.
• Even after certain underlying assumptions, the duration can be used as an appropriate risk measure in normal market conditions.
• Convexity measures can also be incorporated to make it more accurate, and an enhanced version of the price sensitivity formula can be used to measure the sensitivity.

ΔB/B = -D Δy + 1/2 C(Δy)²

Where

• ΔB: Change in bond price
• B: Bond Price
• D: Duration of bond
• C: Convexity of the bond
• Δy: Change in yield (usually taken as 100 bps)

The Convexity in the above formula can be calculated using the below formula:

C_E = P_- + P₊ - 2P₀ / 2(Δy)² P₀

Where

• C_E : Convexity of the bond
• P_: Bond Price with yield down by Δy
• P₊: Bond Price with yield up by Δy
• P_o: Original bond price
• Δy: Change in yield (usually taken as 100 bps)

This has been a guide to what is Duration and its definition. Here we discuss the 3 different ways to arrive at duration measures along with an example, advantages & disadvantages. You can learn more about fixed income from the following articles –

• Modified Duration | Formula
• Calculate YTM
• Cape Ratio