Modified Duration

Publication Date :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

arrow

What is Modified Duration?

Modified Duration tells the investor how much the price of the bond will change, given the change in its yield. As the bond world is more complex than the stock world, the investor needs to know the bond’s modified duration. To calculate the bond’s modified duration, first, the investor needs to figure out one more thing: the Macauley duration. The investor must determine the cash flow timing to calculate the Macaulay Duration.

Table of contents
  • Modified duration is the formula representing the change in the value of a security due to the change in the interest rates. 
  • The main advantage is that the investor must know the bond's duration as the bond price is directly related to the bond prices; the more the bond's duration, the more the price volatility.
  • The modified duration of a fixed-income security is disadvantageous in predicting its price sensitivity to changes in interest rates beyond small changes.
  • Although they have limitations, Modified and Macaulay duration is helpful for portfolio managers for measuring the volatility and the risk associated with the bond. 

Modified Duration Formula

So, the formula for the modified duration is simple.

Modified Duration = Macaulay Duration / (1+YTM/n)

Modified-Duration

Where,

Macaulay Duration= The duration calculates the weighted average time before receiving the bond’s cash flows. Therefore, modified duration is ordered to be calculated first. Then, the investor needs to compute the Macaulay duration of the bond.

YTM = Yield to maturity is simply the total return that the investor would earn in a bond when the bond is held until maturity.

N = Number of coupon periods per year.

Calculation of Modified Duration with Examples

Example #1

A 2-year annual payment of $5,000 bond has a Macaulay duration of 1.87 years. The YTM of the bond is 6.5%. Calculate the modified duration of the bond.

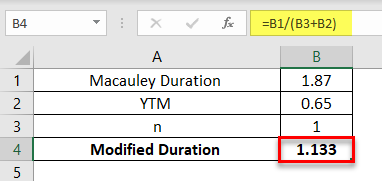
Modified Duration Example 1

Example #2

A 2-year annual payment of $2,000 bond has a Macaulay duration of 2 years. The YTM of the bond is 5%. Calculate the modified duration of the bond.

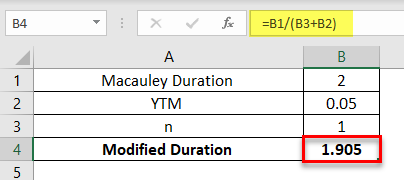
Example 2

Example #3

A 4-year annual payment of $12,000 bond has a Macaulay duration of 5.87 years. The YTM of the bond is 4.5%. Calculate the modified duration of the bond.

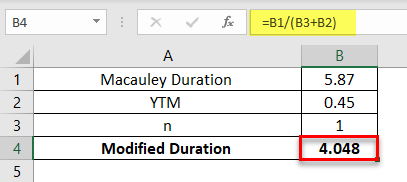
Example 3

Example #4

A 5-year annual payment of $11,000 bond has a Macaulay duration of 1.5 years. The YTM of the bond is 7%. Calculate the modified duration of the bond.

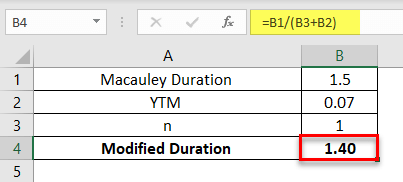
Example 4

Advantages

  • The main advantage is that the investor needs to know the duration of the bond as the bond price volatility is directly related to the bond prices. The greater the bond's duration, the greater the price volatility.
  • The duration of any investment instrument can help manage better investment needs for the future as the investor can effectively plan the future course of its investment in time.
  • It is also a measure of the risk of the bond to the change and the yield in the bond's price.
  • The fund's average duration is also important because it tells how sensitive it will be to market interest rates.

Disadvantages

  • Modified duration calculation is complex because of the Macaulay Duration Calculation. The user or the investor also needs the inputs of yield and tenure to analyze the modified duration.
  • Getting accurate and prevailing inputs in the market is hard to achieve as the price fluctuates every minute, making the calculation incorrect and obsolete.
  • Duration is also not a complete measure of the risk in the bond price and the bond duration. The investor must not solely rely on the duration measure to produce accurate risk measures.
  • Macaulay duration computes the weighted average time of the bond, which is not always a good measure of the risk in the bond.

Conclusion

Modified and Macaulay durations, although limited, are indeed a beneficial concept, especially for the Portfolio Managers to measure the volatility of the bond and the risk associated with it. Hence, it can be helpful when the manager builds a portfolio of bonds and manages the risk associated with them.

Frequently Asked Questions (FAQs)

What is Macaulay duration vs Modified duration?

Macaulay duration refers to the weighted average time before a bondholder receives the bond's cash flows. At the same time, the Modified duration calculates the bond's price sensitivity when the yield of maturity (YTM) changes.

Why is Modified duration better than maturity?

Modified duration is better than maturity because the Modified duration facilitates a clear plan with a prospective effect on a bond price due to a change in the interest rate. In comparison, maturity offers information about the interest rate risk.

What calculating Modified duration involves?

Modified duration calculation divides the dollar value of a basis point change of a series of cash flows or an interest swap leg by the present value of the cash flow series. Then, the value obtained is multiplied by 10,000.