Table Of Contents
What is the Effective Interest Method?
Effective interest method is used for allocating interest expense over the life of financial instruments with the help of standard rate and the market rate of a financial instrument with the aim of reaching to the par value of instrument which is sold either at discount or premium by accumulating and amortizing interest expenditure to carrying value of the financial instrument on systematic and consistent basis respectively.
When the market rate is more than the coupon rate, bonds debentures are sold at a discount as a buyer is willing to pay a lesser price than the market price for the bond. When the market rate is lower than the coupon rate, bonds debentures are sold at a premium. In an ideal situation, the coupon rate exactly matches market-rate means the bond is issued at par value.
Effective Interest Method Formula
The formula for calculation of Effective interest method is as follows,
Effective Interest Rate (r) = (1+i/n)n - 1
Where,
i= rate of interest (coupon rate), n= number of periods per year. If interest is paid semiannually, then the number of years should be divided by 2.

Examples of Effective Interest Method
Below are the examples for calculation of effective interest method -
Example #1 - Bond/ Debenture Issued at Discount
A financial instrument issued at a discount means a buyer has paid lesser value than the par value of the financial instrument. In such a scenario the difference between the amount paid and the book value of the bond is a discount and is amortized over the life of the bond. Every financial instrument carries a rate of interest, which is called a coupon rate paid annually, semi-annually to the bondholder.
The difference between coupon/interest paid and discount amortized is an accretion to bond value. At maturity, carrying a value of a bond will reach the par value of the bond and is paid to the bondholder. Suppose a 5-year $ 100,000 bond is issued with a 9% semiannual coupon in a 10% market $ 96,149 in Jan’17 with interest payout in June and January.
Solution
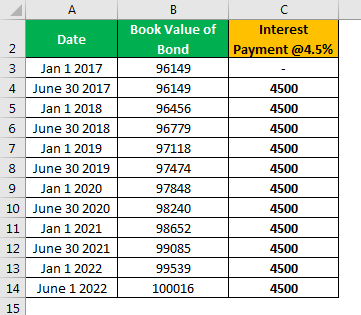
Calculation of Interest Payment
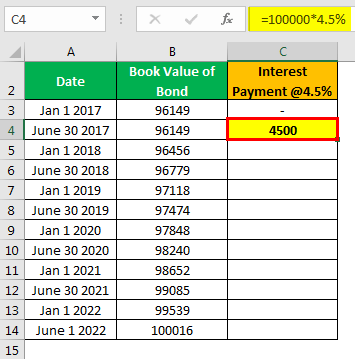
- =100000*4.5%
- =4500
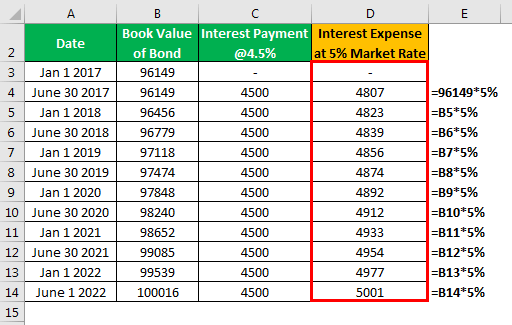
Calculation of Interest Expense
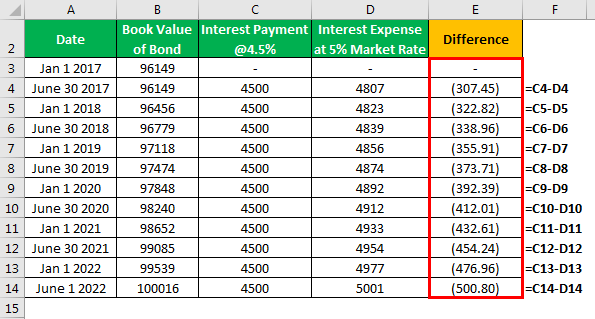
The difference will be as follows -
Accounting Entries for Bonds Issued at a Discount
In the Journal of......(For the period ended on 31st December 2018)
| Date | Particulars | L/F | Debit ($) | Credit ($) |
|---|---|---|---|---|
| 1/1/2017 | Bank A/c...... Dr | 96,149 | ||
| Discount on Issue of Bonds A/c ........Dr | 3,851 | |||
| To Bonds A/c | 100,000 | |||
| (Being 9% semi annual bonds issued in Jan'17) | ||||
| 30/06/2017 | Interest A/c......... Dr | 4,500 | ||
| To Interest Payable A/c | 4,500 | |||
| (Being interest accrued @ 9%) | ||||
| 30/06/2017 | Amortization A/c ........ Dr | 307 | ||
| To Discount on Bonds A/c | 307 | |||
| (Being discount on debentures is amortized over life of bond) | ||||
| Total | 104,807 | 104,807 |
Similar entries will be passed every year. At maturity, Bond, A/c will be debited, and bank A/c will be credited with $ 100,000.
Example #2 - Bond/Debenture Issued at Premium
A financial instrument issued at a premium means a buyer has paid more value than the par value of the financial instruments. In such a scenario, the difference between the amount paid and the book value of a bond is premium and is amortized over the life of the bond. Every financial instrument carries a rate of interest, which is called a coupon rate paid annually, semiannually to the bondholder.
The difference between coupon/interest paid and premium amortized is amortization to carrying the value of a bond. At maturity, the carrying amount of the bond will reach the par value of the bond and is paid to the bondholder. Suppose a 5-year $ 100,000 bond is issued with a 6% semiannual coupon in an 8% market $ 108,530 in Jan’17 with interest payout in June and January.
Solution
Calculation of Interest Payment
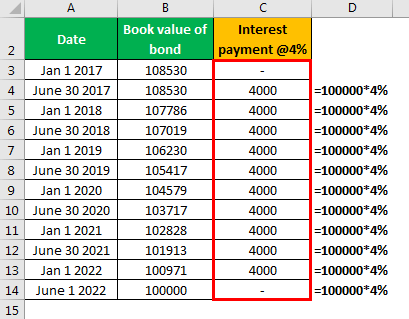
Calculation of Interest Expense
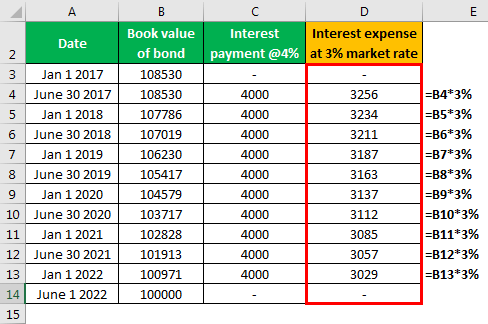
The difference will be as follows -
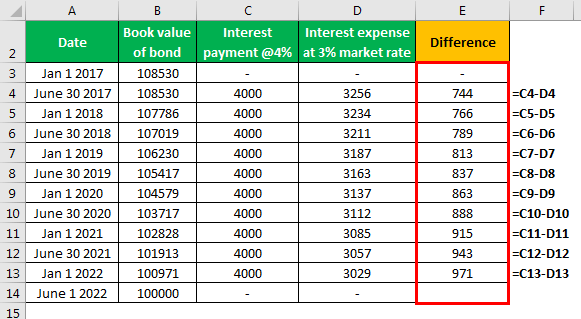
Accounting Entries for Bonds Issued at a Premium
| Date | Particulars | L/F | Debit ($) | Credit ($) |
|---|---|---|---|---|
| 1/1/2017 | Bank A/c...... Dr | 108,530 | ||
| To Bonds A/c | 100,000 | |||
| To Securities Premium A/c | 8,530 | |||
| (Being 8% bonds issued at premium) | ||||
| 30/06/2017 | Interest A/c......... Dr | 4,000 | ||
| To Interest Payable A/c | 4,000 | |||
| (Being interest payable semiannually) | ||||
| 30/06/2017 | Securities premium A/c ........ Dr | 744 | ||
| To Interest A/c | 744 | |||
| (Being premium on bonds recognized over the period of bond) | ||||
| Total | 113,274 | 113,274 |
Similar entries will be passed every year. At maturity, Bond, A/c will be debited, and bank A/c will be credited with $ 100,000.
Example #3 - Bond/Debenture Issued at Par
A financial instrument issued at par means the buyer has paid the exact value for the financial instruments. In such a scenario, the coupon rate is equal to the market rate. Since carrying the value of the bond is exactly equal to the par value of the bond, the effective interest method is not applicable. Normal journal entries will be passed on the issuance of bonds, accrual, and payment of interest, payment of principal amount at maturity.
Practical Applications of Effective Interest Method
- Bonds/debentures issued at discount and premium.
- Calculating the present value of security deposits under IFRS.
- Calculating the present value of minimum lease payments under leasing arrangements.
Advantages And Disadvantages
Advantages
- No sudden charge or income to profit and loss account. Discounts and premiums are spread over the life of the bond.
- Better accounting practices, like the matching concept, is used in this method.
- Future impact on profit and loss accounts is known well in advance, which helps in making a more accurate budget of interest expenditure.
Disadvantages
- A method is more complex than the straight-line method of amortization.
- Not useful for depreciation accounting.
Conclusion
Based on the above discussion, we can conclude that the effective interest method is a more accurate way of calculating interest expenditure than other methods. Although the effective interest method has some limitations, the accounting concept, like the matching concept, is clearly followed in this method.

