Interest Rate Risk

What Is Interest Rate Risk?

Interest rate risk is defined as the risk of change in the value of an asset as a result of volatility in interest rates. It either renders the security in question non-competitive or increases its value. Though the risk is said to arise due to an unexpected move, generally, investors are concerned with downside risk.

This risk directly affects the fixed-rate security holder. Whenever the interest rate rises, the price of the fixed-income bearing security falls and vice-a-versa. Interest rate risk is the primary driver of the markets. It has a direct impact on fixed-income bearing securities and an indirect impact on share prices. It also impacts foreign exchange rates directly.

• Interest rate risk refers to the potential impact of changes in interest rates on the value of fixed-income securities, such as bonds and loans.
• When interest rates rise, the value of existing fixed-rate securities generally declines because their coupon rates become less attractive than newly issued securities with higher rates. Conversely, when interest rates fall, the value of existing fixed-rate securities tends to rise.
• Longer-term fixed-income securities typically carry higher interest rate risk than shorter-term securities because there is more time for interest rate changes to affect their value.

Interest Rate Risk Explained

The concept of interest rate risk management involves dealing with the probability of loss in business or individual portfolios due to fluctuation of interest rates in the financial market. In case the rates rise, the value of the investments made in fixed incomes or bonds declines in the secondary market. This means that the existing bonds face a fall in prices, offsetting the new high rates.

Diversification of a portfolio is a very effective way to hedge or protect against the fluctuation in the rates because the fall in price of one asset is compensated by the rise in the other. Security holders and analysts regularly track and analyse these changes to understand the market movements and their impact on the overall financial market.

The duration of financial instruments like bonds has different impacts due to changes in rates, which also depends on the type of interest, which can be fixed or floating. But long-term bond interest rate risk is usually more, and thus they have higher interest rates to compensate for losses on fluctuations in interest rates.

There are a lot of ways to hedge these risks, and the market offering such products is highly liquid and efficient. Although there is a cost involved for hedging interest rate risk in the form of brokerages, premium, etc. but the benefits might outweigh the costs in most of the time.

Example

Let us understand interest rate risk management through an example.

If an investor has invested some amount in a fixed rate, the bond at the prevailing price, which offers him a coupon rate of 5%, and if thereafter interest rises to 6%, then the price of the bond would decline. This is because the bond is offering a rate of 5% while the market is offering a rate of return of 6%. Hence if the investor wants to sell this bond in the market, the buyer would offer him a lesser amount for the bond as this bond is low-yielding as compared to the market. By doing this, the new investor would try to earn a return similar to the market as the invested amount is less.

In other words, the opportunity cost of getting a better return elsewhere increases with an increase in the interest rate. Hence it results in a decline in bond price.

There are various ways to calculate interest rate risk and combat it. For example, one can buy interest rate swaps, call or put options for the securities or invest in the negatively correlated securities to hedge the risk.

Impact Of Interest Rate Change On Bonds

Interest rate change impacts bonds with different maturities, to a different extent. The correlation between interest rate move and a movement in the price gets stronger with the increase in maturity. This is so because, in case of a rise in interest rate, the bond with a longer maturity will suffer a lower rate of interest for a longer time as compared to a bond with shorter maturity. That’s why investing in bonds with different maturities is used as a hedging technique to combat the interest rate risk.

Interest rate change impacts coupon bonds and zero-coupon bonds differently. If we consider both types of bond interest rate risk with the same maturity, we will experience a sharper decline in the price of zero-coupon bonds due to the interest rate rise as compared to the coupon bond. This is because the whole amount will be received at the end of the stipulated period in case of a zero-coupon bond. Hence, it increases the effective duration. In contrast, the returns are generated periodically in the case of coupon bonds, and hence, it reduces the effective duration of repayment.

Interest rate risk is also impacted by the coupon rate. The bond with a lower coupon rate has a higher interest rate risk as compared to a bond with a higher interest rate. This is so, as a small change in the market interest rate can easily outweigh the lower coupon rate and will reduce the market price of that bond.

Types

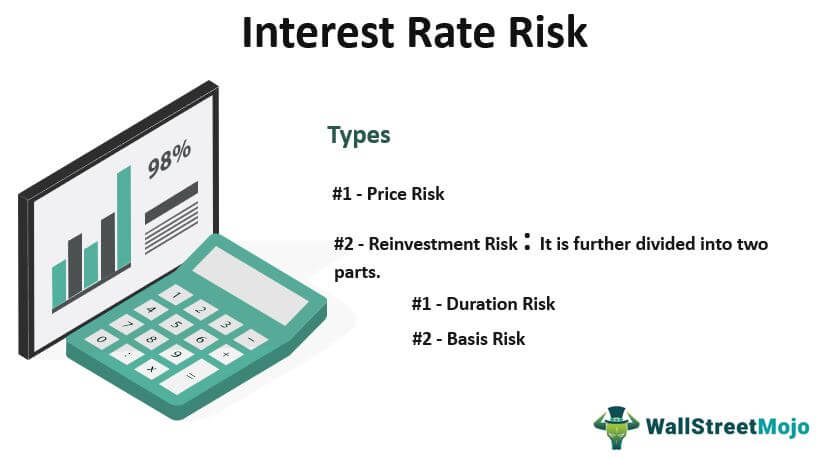
There are two types of interest rate risk:

#1 - Price Risk

It is the risk of change in the price of the security, which may result in an unexpected gain or loss when the security is sold.

#2 - Reinvestment Risk

It refers to the risk of change in the interest rate, which may lead to the non-availability of the opportunity to reinvest in the current investment rate. It is further divided into two parts -

• #1 - Duration Risk - It refers to the risk arising from the probability of unwilling pre-payment or extension of the investment beyond the predetermined time period.
• #2 - Basis Risk - It refers to the risk of not experiencing the exact opposite behavior to interest rate changes in the securities with inverse features.

Duration And Change In Price

The duration of the security directly relates to the extent to which a change in interest rate will impact the price. It is different from maturity. It calculates the expected change in the price as a result of a 1% change in interest rates. It approximates the price elasticity of demand. It is calculated by adding the product of the time period of cash flow and the respective weights, which are calculated on the basis of the present value of cash flows.

Example

A five-year bond with a face value of $100 is issued with a coupon rate of 6%. It has a semi-annually compounded market yield of 8%. Calculate duration.

Solution:

The coupon payment is made on a half-yearly basis. Hence, cash flow after every 6 months would be half of 6%, i.e., $3.

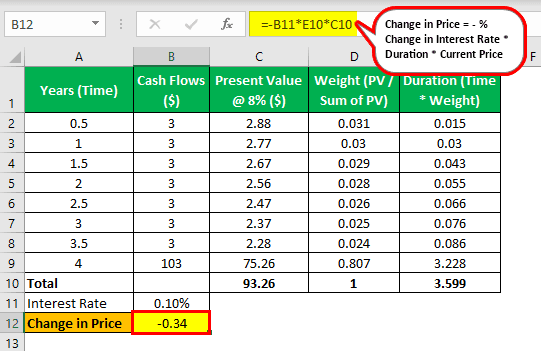
Hence, the duration of this bond is 3.599 years, whereas maturity is 4 years. The price of the bond is the sum total of the present value of all the cash flows, which is $93.27.

Change in price is proportional to the change in interest rate, which is calculated by using the following formula:

So, if the % increase in interest rate is 0.1%, then in the above example, the change in the price would be: -0.1% * 3.599 * 93.27 = -$0.34

New price of the bond would be = $93.27 - $0.34 = $92.93.

You can refer to the above given excel template for the detailed calculation of interest rate risk.

Advantages

Like any other financial concept, this also has its own advantages and disadvantages. Let us first try to understand the advantages of the concept.

• Measuring interest rate risk helps to gain from favorable interest rate movements.
• Arbitrage gain by operating in multiple markets.
• Creation of an efficient market platform through the introduction of participants like insurers.

Disadvantages

Some disadvantages of the same are as follows:

• The potential loss from unexpected interest rate movements.
• Increased cost viz. hedging cost, administration cost, etc.

How To Hedge?

As explained, it is a form of risk that individuals and businesses need to bear from time to time. There are ways to protect against such risk of loss. Let us go through them.

• Fixed rate instruments – They help to set off the losses incurred from already holding bonds with lower rate. The investor can invest in new bonds in case there is a chance of the rates to go up.  
• Interest rate swap – It involves exchanging cash flows with another party. This allows convertibility of fixed to floating and vice versa.
• Futures and options contracts – They are an excellent method of measuring interest rate risk and hedging against possible interest rate fluctuations. These contracts lock the interest for a certain period. Therefore, in case of a rise in rates, the contract value rises, offsetting the loss.  
• Diversification – This helps to calculate interest rate risk and mitigate the negative impact against the risk because the loss of one investment is compensated by the gain from the other.
• Duration – The time period plays a big role. Investments held for long term usually helps in reducing the loss because there might be a rise as well as a fall in rates in the long term.

Frequently Asked Questions (FAQs)

Recommended Articles

This has been a guide to what is Interest Rate Risk and its definition. Here we discuss its types, example of interest rate risk along with its advantages and disadvantages. Here we also calculate duration and change in price due to the interest rate change.  You can learn more about accounting from the following articles –

• How Equity Swaps Works?
• Reinvestment Risk Definition
• What is the Carrying Value of Bond?
• What is Bond Sinking Fund?