Table Of Contents
Correlation Examples in Statistics
An example of a positive correlation includes calories burned by exercise, where with the increase in the exercise level, the calories burned will also increase. On the other hand, an example of the negative correlation includes the relationship between steel prices and the prices of shares of steel companies, wherewith the increase in prices of the steel share price will decrease.
In statistics, the Correlation mainly analyzes the strength of the relationship between the variables under consideration. However, it also measures if there is any linear relationship, i.e., linear, between the given sets of data and how well they could be related. One such common measure used in the field of statistics for correlation is the Pearson Correlation Coefficient. The following correlation example provides an outline of the most common correlations.
Example #1
Vivek and Rupal are siblings. Rupal is older than Vivek by three years. Sanjeev, their father, is a statistician, and he was interested in researching the linear relationship between height and weight. Hence, since their birth, he noted their height and weight at various ages and arrived at the following:
| Age | Rupal | Vivek | ||
|---|---|---|---|---|
| Height (in foot) | Weight (in Kgs) | Height (in foot) | Weight (in Kgs) | |
| 5 | 3.5 | 20 | 3.6 | 22 |
| 7 | 3.11 | 25 | 3.101 | 27 |
| 9 | 4.1 | 26 | 4.3 | 28 |
| 11 | 4.7 | 32 | 4.7 | 32 |
| 13 | 4.11 | 35 | 4.11 | 40 |
| 15 | 5.1 | 40 | 5.2 | 45 |
| 17 | 5.2 | 45 | 5.4 | 50 |
| 19 | 5.3 | 48 | 5.7 | 55 |
| 21 | 5.5 | 50 | 5.9 | 64 |
| 23 | 5.55 | 51 | 5.9 | 67 |
| 25 | 5.55 | 55 | 5.9 | 70 |
He tries to identify any correlation between age, height, and weight, and is there any differentiation between them?
Solution:
We will first plot a scatter chart. We get below the result for Rupal’s and Vivek’s age, height, and weight.

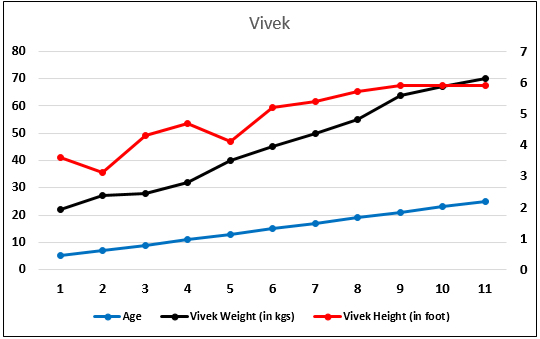
As age increases, height increases, and weight increases, so there appears to be a positive relationship. In other words, height and age are positive correlations. Further, Sanjeev observed that weight fluctuates and is not stable. It could either increase or decrease marginally, but he observed a positive relationship between height and weight; weight also tends to increase when height increases.
Thus, he observed two crucial relationships here: with age – height increases, and weight increases with height increases. Hence, all three-carry positive correlations.
Example #2
John is excited about summer vacation. However, his parents are worried since the teenager would be sitting home and playing games on his mobile and switching on the air conditioner the whole time. They noted the various temperatures and the units consumed last year and found interesting data. And they wanted to anticipate their upcoming may month bill and expect the temperature to be near 40*C. Still, they want to know if there is any correlation between temperature and electricity bills.
| Temperature (in oC) | Units Consumed | Electricity Bill (in Rs) |
|---|---|---|
| 24 | 80 | 2,490.00 |
| 27 | 82 | 2,550.00 |
| 30 | 84 | 2,610.00 |
| 31 | 101 | 3,170.00 |
| 34 | 110 | 3,890.00 |
| 35 | 115 | 4,290.00 |
| 38 | 140 | 6,390.00 |
| 40 | 142 | 6,441.00 |
| 42 | 156 | 7,155.00 |
| 45 | 157 | 7,206.00 |
Solution:
Let’s analyze this as well through a chart.

We have plotted electricity bills and temperature and noted their various points. There appears to be a correlation between the temperature and the electricity bill when the temperature is cold. The electricity bill is under control, making sense as the family would use less air conditioner. As and when temperature increases, air conditioners, and geysers would increase, which would hit them with a higher cost, evident from the above graph where the electricity bill rises heavily.
Thus, we can conclude that there is no linear relationship, but yes, there is a positive correlation. Hence, the family can again expect a bill amount for may in the range of 6400 to 7000.
Example #3
Tom has started a new catering business, where he first analyzes the cost of making a sandwich and what price he should sell them. After talking to various cooks currently selling the sandwich, he has gathered the information below. Tom was convinced that there is a positive linear relationship between the number of sandwiches and the total cost of making them. Analyze if this statement is true.
| No of Sandwich | Cost of Bread | Vegetable | Total Cost |
|---|---|---|---|
| 10 | 100 | 30 | 130 |
| 20 | 200 | 60 | 260 |
| 30 | 300 | 90 | 390 |
| 40 | 400 | 120 | 520 |
Tom convinces a positive linear relationship between the number of sandwiches and the total cost of making them. Analyze if this statement is true.
Solution:
After plotting the points between the number of sandwiches prepared and the cost of making them, there is a positive relationship.

And it can be seen from the above table that yes, there is a positive linear relationship. If one runs correlation, it will come to +1. Hence, as Tom makes more sandwiches, the cost will increase, and it appears valid as one will require the more the sandwich, the more vegetables, and so would bread be required. Hence, this has a positive perfect linear relationship based on the data.
Example #4
Rakesh has been investing in ABC stock for quite a long time. He wants to know whether ABC stock is a good hedge for the market as he has also invested in an ETF fund that tracks a market index. He has gathered the below data for the past 12 monthly returns on the stock ABC and index.
Using correlation, identify the relationship ABC stock has with the market and whether it hedges the portfolio.
| Month | Change in Price of ABC Stock | Change in Price Index |
|---|---|---|
| Jan | -4.00% | 2.00% |
| Feb | -3.86% | 2.33% |
| Mar | 1.21% | 0.09% |
| Apr | -0.33% | 1.01% |
| May | 6.00% | -0.34% |
| Jun | 7.00% | -3.40% |
| Jul | 4.55% | -1.50% |
| Aug | 3.50% | -1.09% |
| Sep | 1.50% | 2.50% |
| Oct | -4.00% | 3.00% |
| Nov | -3.50% | 2.89% |
| Dec | -5.00% | 4.00% |
Solution:
Using the correlation coefficient formula below treating ABC stock price changes as x and changes in markets index as y, we get a correlation of -0.90.

It is a close-to-perfect negative correlation. In other words, a negative relationship.
Therefore, as the market rises, the stock price of ABC falls, and when the market falls, the stock price of ABC rises. Hence, it is a good hedge for the portfolio.
Conclusion
One can conclude that there could be a correlation between two variables but not necessarily a linear relationship. For example, there could be exponential correlation or log correlation. Hence, if one gets a result stating a positive or negative correlation, then it should be judged by plotting the variables on the graph and finding out if there is truly any relationship or a spur correlation.
