Pearson Correlation Coefficient

Pearson Correlation Coefficient Definition

Pearson correlation coefficient, also known as Pearson R statistical test, measures strength between the different variables and their relationships. Whenever any statistical test is conducted between the two variables, then it is always a good idea for the person doing analysis to calculate the value of the correlation coefficient for knowing that how strong the relationship between the two variables is.

Pearson’s correlation coefficient returns a value between -1 and 1. The interpretation of the correlation coefficient is as under:

• If the correlation coefficient is -1, it indicates a strong negative relationship. It implies a perfect negative relationship between the variables.
• If the correlation coefficient is 0, it indicates no relationship.
• If the correlation coefficient is 1, it indicates a strong positive relationship. It implies a perfect positive relationship between the variables.

A higher absolute value of the correlation coefficient indicates a stronger relationship between variables. Thus, a correlation coefficient of 0.78 indicates a stronger positive correlation as compared to a value of say 0.36. Similarly, a correlation coefficient of -0.87 indicates a stronger negative correlation as compared to a correlation coefficient of say -0.40.

In other words, if the value is in the positive range, then it shows that the relationship between variables is correlated positively, and both the values decrease or increase together. On the other hand, if the value is in the negative range, then it shows that the relationship between variables is correlated negatively, and both the values will go in the opposite direction.

Pearson Correlation Coefficient Formula

Pearson’s Correlation Coefficient formula is as follows,

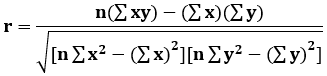
Where,

• r = Pearson Coefficient
• n= number of the pairs of the stock
• ∑xy = sum of products of the paired stocks
• ∑x = sum of the x scores
• ∑y= sum of the y scores
• ∑x² = sum of the squared x scores
• ∑y² = sum of the squared y scores

Explanation

Step 1: Find out the number of pairs of variables, which is denoted by n. Let us presume x consists of 3 variables – 6, 8, 10. Let us presume that y consists of corresponding 3 variables 12, 10, 20.

Step 2: List down the variables in two columns.

Step 3: Find out the product of x and y in the 3^rd column.

Step 4: Find out the sum of values of all x variables and all y variables. Write the results at the bottom of 1^st and 2^nd column. Write the sum of x*y in the 3^rd column.

Popular Course in this category

Financial Modeling Course (with 15+ Projects)
4.9 (927 ratings) 16 Courses | 15+ Projects | 90+ Hours | Full Lifetime Access | Certificate of Completion

View Course

Step 5: Find out x² and y² in the 4^th and 5^th columns and their sum at the bottom of the columns.

Step 6: Insert the values found above in the formula and solve it.

r = 3*352-24*42/√(3*200-24²)*(3*644-42²)

= 0.7559

Example of Pearson Correlation Coefficient R

Example 1

In this example with the help of the following details in the table of the 6 people having a different age and different weights given below for the calculation of the value of the Pearson R

Solution:

For the Calculation of the Pearson Correlation Coefficient, we will first calculate the following values,

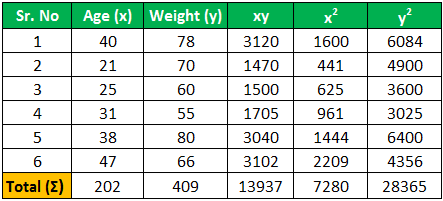
Here the total number of people is 6 so, n=6

Now the calculation of the Pearson R is as follows,

• r = (n (∑xy)- (∑x)(∑y))/(√ [n ∑x²-(∑x)²][n ∑y²– (∑y)² )
• r = (6 * (13937)- (202)(409)) / (√ [6 *7280 -(202)²] * [6 * 28365- (409)² )
• r = (6 * (13937)- (202) * (409))/(√ [6 *7280 -(202)²] * [6 * 28365- (409)² )
• r = (83622- 82618)/(√ [43680 -40804] * [170190- 167281 )
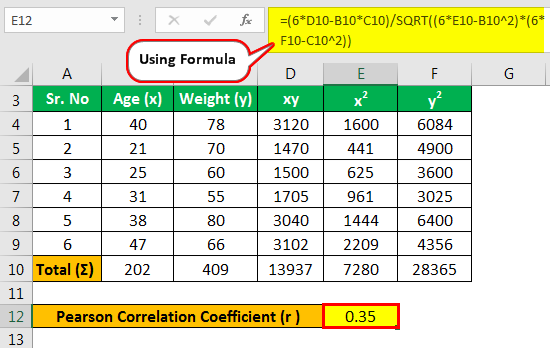
• r = 1004/(√ [2876] * [2909 )
• r = 1004 / (√ 8366284)
• r = 1004 / 2892.452938
• r = 0.35

Thus the value of the Pearson correlation coefficient is 0.35

Example #2

There are 2 stocks – A and B. Their share prices on particular days are as follows:

Find out the Pearson correlation coefficient from the above data.

Solution:

First, we will calculate the following values.

The calculation of the Pearson coefficient is as follows,

• r = (5*1935-266*37)/((5*14298-(266)^2)*(5*283-(37)^2))^0.5
• = -0.9088

Therefore the Pearson correlation coefficient between the two stocks is -0.9088.

Advantages

• It helps in knowing how strong the relationship between the two variables is. Not only the presence or the absence of the correlation between the two variables is indicated using the Pearson Correlation Coefficient but it also determines the exact extent to which those variables are correlated.
• Using this method, one can ascertain the direction of correlation i.e. whether the correlation between two variables is negative or positive.

Disadvantages

• The Pearson Correlation Coefficient R is not sufficient to tell the difference between the dependent variables and the independent variables as the Correlation coefficient between the variables is symmetric. For example, if a person is trying to know the correlation between the high stress and blood pressure, then one might find the high value of the correlation which shows that high stress causes the blood pressure. Now if the variable is switched around then the result, in that case, will also be the same which shows that stress is caused by the blood pressure which makes no sense. Thus, the researcher should be aware of the data that he is using for conducting the analysis.
• Using this method one cannot get the information about the slope of the line as it only states whether any relationship between the two variables exists or not.
• It is likely that the Pearson Correlation Coefficient may be misinterpreted especially in case of the homogeneous data.
• When compared with the other methods of the calculation, this method takes much time for arriving at the results.

Important Points

• The values can range from the value +1 to the value -1, where the +1 indicates the perfect positive relationship between the variables considered, the -1 indicates the perfect negative relationship between the variables considered, and a 0 value indicates that no relationship exists between the variables considered.
• It is independent of the unit of measurement of the variables. For example, if the unit of measurement of one variable is in years while the unit of measurement of the second variable is in kilograms, even then, the value of this coefficient does not changes.
• The correlation coefficient between the variables is symmetric which means that the value of the correlation coefficient between Y and X or X and Y, will remain the same.

Conclusion

Pearson Correlation Coefficient is the type of the correlation coefficient which represents the relationship between the two variables which are measured on the same interval or same ratio scale. It measures the strength of the relationship between the two continuous variables.

It not only states the presence or the absence of the correlation between the two variables but it also determines the exact extent to which those variables are correlated. It is independent of the unit of measurement of the variables where the values of the correlation coefficient can range from the value +1 to the value -1. However, it is not sufficient to tell the difference between the dependent variables and the independent variables.

Recommended Articles

This has been a guide to the Pearson Correlation Coefficient and its definition. Here we discuss how to calculate the Pearson Correlation Coefficient R using its formula and example. You can learn more about excel modeling from the following articles –

• Correlation Examples
• Correlation vs Covariance
• Multicollinearity
• CORREL Excel Function (Correlation)