Correlation Formula

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Correlation Meaning

The correlation formula is applied to understand the movement of two data points in relation to each other. In the world of finance and investing, the two data points are usually securities. It is closely associated with the diversification of a portfolio, a method that is used to mitigate risk and spread investments across different asset classes.

The correlation formula statistics help investors and analysts compare a particular stock in relation to the index to see if the performance is correlated. However, it is important to understand that this metric does not show if A caused B or if it was influenced by an external factor. It is computed as a correlation coefficient that should range between -1.0 and +1.0.

Correlation Formula Explained
Examples
Relevance and Use
Recommended Articles

Correlation Formula Explained

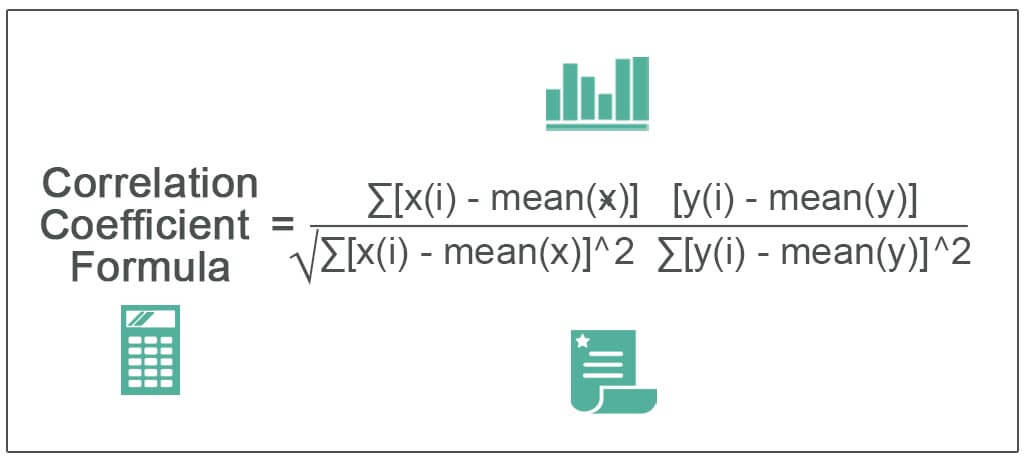
Correlation is a statistical measure between two variables. One may define it as the change of quantity in one variable corresponding to a change in another. One can calculate it by summation of the product of the sum of the first variable minus the mean of the first variable into a sum of the second variable minus the mean of the second variable divided by the whole under the root of the product of the square of the first variable minus the mean of the first variable into the sum of the square of second variable minus the mean of the second variable.

The value of a simple correlation formula is limited between -1 and +1 and can be interpreted as follows:

-1: If it is -1, then variables are known as perfectly negatively correlated. That means if one variable is moving in one direction, another is moving in the opposite direction.
0: That means the variable is not having any correlation.
+1: If it is +1, then variables are known as perfectly positively correlated. Both variables are moving in positive directions.

A perfect correlation implies that the movement in one variable shall result in the exact same movement in the other variable too in the same direction. While there are various methods of calculating this metric, the most widely used method of calculation is the Pearson product-moment correlation.

However, in the modern day, investors, market experts, and analysts use the CORREL function in MS Excel to avoid doing complex calculations which can be time-consuming and have a high possibility of errors.

Formula

If we have two variables, x, and y, then the correlation coefficient between 2 variables can be found as:

Correlation Coefficient = ∑(x(i)- mean(x))*(y(i)-mean(y)) / √ (∑(x(i)-mean(x))² * ∑(y(i)-mean(y))²)

Where,

x(i)= value of x in the sample
Mean(x) = mean of all values of x
y(i) = value of y in the sample
Mean(y) = mean of all values of y

Examples

Let us understand the correlation formula statistics with the help of a few examples as discussed below. These examples shall give us a practical overview of the concept and its related factors.

It is effortless to calculate the correlation in Excel. The syntax of the function used is as follows:

Correlation Coefficient = CORREL (array1, array2)

Example#1

Let’s take the same example above for calculating correlation using Excel.

Solution:

Below are the values of x and y:

The calculation is as follows.

Basis Excel formula = CORREL (array(x), array(y))

Coefficient = +0.95

Since this coefficient is near +1, x and y are highly positively correlated.

Example#2

Correlation is mainly useful for analyzing companies' stock prices and creating a stock portfolio based on that.

Let us determine the correlation of Apple stock with the Nasdaq index based on the last one-year stock performance. Apple is a US-based multinational company specializing in IT products such as iPod, iPad, Mac, etc.

Solution:

Below is the monthly return of Apple and Nasdaq stocks for the last year:

Let’s now input the values -

Correlation Coefficient = ∑(x(i)- mean(x)).(y(i)-mean(y))/√ ∑(x(i)-mean(x)) ^² ∑(y(i)-mean(y))^²

Correlation between Apple and Nasdaq= 0.039/ (√0.0039)

Coefficient =0.62

Since the correlation between Apple and Nasdaq is positive. Hence, Apple positively correlates with Nasdaq

Example#3

Let us now examine the correlation between Walmart and the Nasdaq index based on last year's stock performance. Walmart is a US-based company which has a retail supermarket chain.

Solution:

Below is the monthly performance between Walmart and Nasdaq for the last year:

Let’s now input the values in the formula: -

Correlation Coefficient = ∑(x(i)- mean(x)).(y(i)-mean(y))/√ ∑(x(i)-mean(x)) ^² ∑(y(i)-mean(y))^²

Therefore, the calculation is as follows:

Correlation between Walmart and Nasdaq= 0.0032/ (√0.0346*0.0219 )

Coefficient =0.12

We can see that Walmart and Nasdaq are positively correlated but not as much compared to Apple's correlation with Nasdaq.

Relevance and Use

Let us understand the relevance and uses of applying the simple correlation formula to security and gauging its movements in accordance with the other variable through the points below.

A correlation coefficient is useful in establishing the linear relationship between two variables.
It measures how a variable will move compared to the movement of another variable. For example, the practical use of this coefficient is to find out the relationship between stock price movement with the overall market movement. Based on this analysis, a stock analyst will include the proportion of stocks to create an optimal portfolio with minimum risk. Also, it is useful in data science to find the relationship between 2 variables.
Also, the correlation coefficient is used very highly for studying the construct validity of data in factor analysis. Furthermore, it is highly used in regression analysis to predict the values of dependent variables based on the relationship between dependent and independent variables.
Finally, this equation is useful in quantitative analysis to determine the relationship between various variables. The basis of this relationship, if a variable is unrelated to other variables, it can be eliminated from the list.

Correlation Vs Regression

While both correlation formula statistics and regression are widely followed numbers for their individual importance, it is important to understand the differences in their fundamentals and implications to completely understand the concept. Let us do so through the comparison below.

Correlation

It refers to the relationship between two or more variables.
X and Y are not fixed variables, they are random in nature.
The range of the correlation or relationship lies between -1.0 to +1.0.
This metric gives very limited information after the relationship between the variables is established.
Therefore, it is the study of the linear relationship of the variables.
Its objective is to find the numerical value that can be a representation of the relationship between the variables.

Regression

Regression measures the average relationship between two or more variables.
Here X is a random variable, whereas, Y is a fixed variable.
It is expressed as an absolute figure.
It is used to determine or predict the value of the other variable based on the value of the given variable.
It is the study of the linear and non-linear relationship between the variables.
Its objective is to find or predict the values of a random variable based on the value of the fixed variable.