NPV vs XNPV | Top Differences with Excel Examples

Net Present Value (NPV) is defined as the difference between the existing value of net cash arrivals and the existing value of total cash expenditures.  While NPV is most helpful in the case of periodic cash flows, XNPV, on the other hand, determines the Net Present Value for a range of cash payments that need not be essentially periodic.

In this article, we look at NPV vs XNPV in detail -

Also, have a look at NPV vs IRR

Net Present Value (NPV) is defined as the difference between the existing value of net cash arrivals and the existing value of total cash expenditures. NPV is generally used while preparing capital budgeting estimates for accurately determining the viability of any new project or a prospective investment opportunity.

The formula for determining NPV (when cash arrivals are even):

NPV_{t=1 to T}  = ∑  Xt/(1 + R)^t - Xo

Where,

• X_t = total cash inflow for period t
• X_o = net initial investment expenditures
• R = discount rate, finally
• t = total time period count

The formula for determining NPV (when cash arrivals are uneven):

NPV = - X_o

Where,

• R is the specified return rate per period;
• C_i1 is the consolidated cash arrival during the first period;
• C_i2 is the consolidated cash arrival during the second period;
• C_i3 is the consolidated cash arrival during the third period, etc…

For individual projects, take a project simply when its NPV is calculated as positive, discard it if project NPV is calculated as negative, and remain indifferent towards considering or discarding if project NPV arrived at zero.

For completely different projects or competing projects, consider the project having greater NPV.

Net present value with a positive sign signifies that the estimated earnings delivered by any investment opportunity or a project (in existing dollar denominations) surpass the projected expenditures (also in existing dollar values). Usually, any investment having positive NPV results is bound to be a lucrative one, while one having negative NPV results would lead to an overall loss. This idea particularly defines the Net Present Value Rule, indicating that only those investments must be considered that have positive NPV results.

In addition, suppose the investment opportunity is related to a merger or an acquisition, one may even employ the Discounted Cash Flow.

Besides the NPV formula, the net present value may even be calculated by leveraging spreadsheets, tables like Microsoft Excel as well as the NPV calculator.

Using NPV in the excel sheet is very easy.

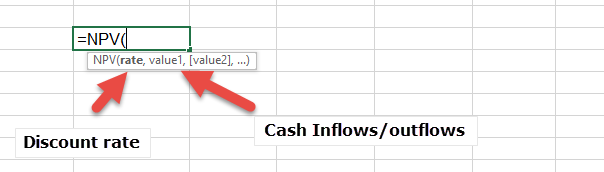
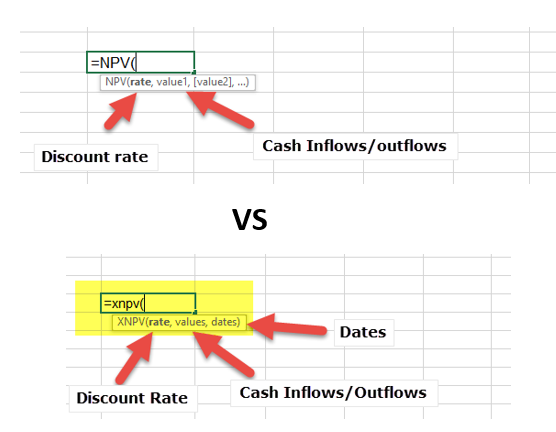
= NPV (Rate, Value1, Value2, Value3..)

• The rate in the formula is the discount rate that is used in one period.
• Value 1, Value 2, Value 3, etc. are the cash inflows or outflows at the end of periods 1, 2, 3, respectively.

Suppose a company is keen on analyzing the estimated viability of a key project that demands an early outflow of $20,000. Over the three years period, the project seems to deliver revenues of $4000, $14,000, and $22,000, respectively. The projected discount rate expects to be 5.5%. At initial glance, it appears that the investment returns are almost double the initial investment. But, the amount earned over three years remains not of the same value as the net amount earned today. Hence the accountant of the company determines the NPV in a unique way of identifying the overall profitability whereas calculating the reduced time value of estimated revenues:

NPV Example #1 - Solution using Manual Calculation

To calculate Net Present Value, one should remember the following points:

• Addition of the Present Value received
• Deduction of the Present Value being paid

NPV = {$4,000/(1+.055)^1} + {$14,000/(1+.055)^2} + {$22,000/(1+.055)^3} - $20,000

= $3,791.5 + $12,578.6 + $18,739.4 - $20,000

= $15,105.3

NPV Example #1 - Solution using Excel

Solving NPV problems in Excel are very easy. First, we need to put the variables in the standard format as given below with Cash Flows in one row.

In this example, we are provided with a discount rate of a yearly discount rate of 5.5%. When we use NPV Formula, we start with $4000 (cash inflows at the end of year 1) and choose the range until $22,000 (

When we use NPV Formula, we start with $4000 (cash inflows at the end of year 1) and choose the range until $22,000 (corresponding to the cash inflows of year 3)

The Present Value of Cash Flows (year 1, 2, and 3) is $35,105.3

Cash invested or the Cash outflow in Year 0 is $20,000.

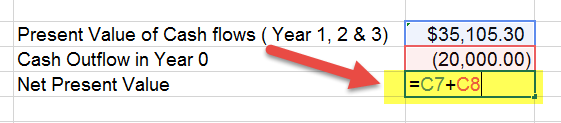
When we deduct the cash outflow from the present value, we get the Net Present Value as $15,105.3

Determine a project’s net present value that needs an early investment worth $245,000 while it is estimated to deliver a cash arrival of $40,000 every month for the forthcoming 12 months. The remaining project value is assumed to be zero. The expected return rate is 24% per annum.

NPV Example #2 - Solution using Manual Calculation

Given,

Early investment = $245,000

Overall cash arrival per period = $40,000

Period count = 12

Discount Rate for each period = 24%/12 = 2%

NPV Calculation:

= $40,000*(1-(1+2%) ^-12)/2% - $245,000

= $178,013.65

NPV Example #2 - Solution using Excel

Like we did in our earlier example, the first thing we will do is to put the cash inflows and cash outflows in the standard format as per given below.

There are some important things to note in this example -

1. In this example, we are provided with monthly cash inflows, whereas the discount rate provided is that of the full year.
2. In the NPV formula, we need to ensure that the discount rate and the cash inflows are in the same frequency, meaning if we have monthly cash flows, then we should have a monthly discount rate.
3. In our example, we will work around the Discount Rate and convert this yearly discount rate into a monthly discount rate.
4. Yearly Discount Rate = 24%. Monthly Discount Rate = 24% / 12 = 2%. We will use a 2% discount rate in our calculations

Using these monthly cash inflows and a monthly discount rate of 2%, we calculate the present value of the future cash flows.

We get the present value of monthly cash inflows as $423,013.65

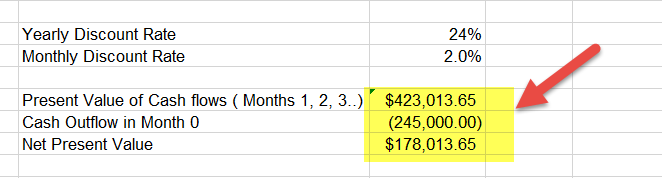
Cash Invested or Cash outflow in Month 0 was $245,000.

With this, we get the Net Present Value of $178,013.65

The XNPV function in excel primarily determines the Net Present Value (NPV) for a range of cash payments that need not be essentially periodic.

XNPV_{t=1 to N}  = ∑  Ci/

Where,

• d_x = the x’th expense date
• d_o = the date for 0’th expense
• C_i = the i’th expense

The XNPV function in Excel employs the following formula for calculating the net present value of any investment opportunity:

XNPV(R, Value Range, Date Range)

Where,

R = discount rate for cash flows

Value Range = A set of numeric data, depicting income and payments, where:

• Positive figures are identified as income;
• Negative figures are identified as payments.

The first disbursement is discretionary and signifies a payment or expense at the start of an investment.

Date Range = A range of dates equivalent to a series of expenditures. This payment array should match with the array of supplied values.

We will take the same example that we took earlier with NPV and see if there is any difference between the two approaches of NPV vs XNPV.

Suppose a company is keen on analyzing the estimated viability of a key project that demands an early outflow of $20,000. Over the three years period, the project seems to deliver revenues of $4000, $14,000 and $22,000, respectively. The projected discount rate expects to be 5.5%.

First, we will put the cash inflows and outflows in the standard format. Please note here that we have also put the corresponding dates along with the Cash Inflows and Outflows.

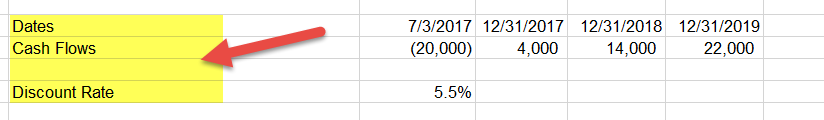
The second step is to calculate by providing all the necessary inputs for XNPV - Discount Rate, Value Range and Date Range. You will note that in this XNPV formula, we have also included the cash outflows done today.

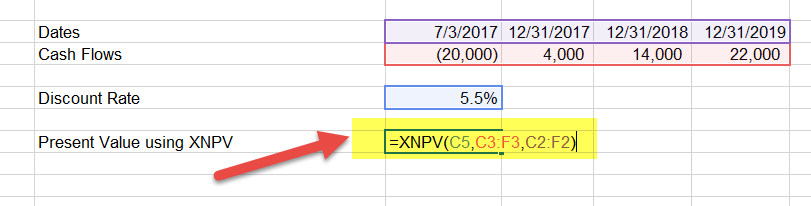
We get the Present value using XNPV as $16,065.7.

With NPV, we got this Present Value as $15,105.3

The present Value using XNPV is higher than that of NPV. Can you guess why we get different present values under NPV vs XNPV?

The answer is simple. NPV assumes that future cash inflows happen at the end of the year (from today). Let's assume that today is 3rd July 2017, then the first cash inflow of $4000 is expected to come after one year from this date. This means you get $4,000 on 3rd July 2018, $14,000 on  3rd July 2019, and $22,000 on 3rd July 2020.

However, when we calculated the present value using XNPV, the cash inflow dates were the actual year-end dates. When we use XNPV, we are discounting the first cash flow for a period that is less than one year. Likewise, for others. This results in the Present Value using the XNPV formula to be greater than that NPV formula.

We will take the same NPV Example 2 to solve using XNPV.

Determine a project’s net present value that needs an early investment worth $245,000 while it is estimated to deliver a cash arrival of $40,000 every month for the forthcoming 12 months. The remaining project value is assumed to be zero. The expected return rate is 24% per annum.

The first step is to put the cash inflow and outflows in the standard format shown below.

In the NPV example, we converted our yearly discount rate into the monthly discount rate. For XNPV, we are not required to do this extra step. We can directly use the yearly discount rate.

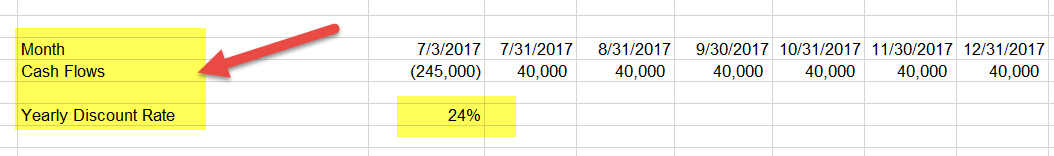
The next step is to use the discount rate; cash flows range, and date range in the formula. Please note that we have also included cash outflows that we did today in the formula.

The present Value using the XNPV formula is $183,598.2

Contrasting this with that of NPV Formula, the present value using NPV is $178,013.65

Why there XNPV formula yields present value higher than that of NPV? The answer is simple, and I leave it to you to contrast NPV vs XNPV in this case.

Now let us take another example with NPV vs XNPV head to head. Let us assume that we have the following cash flow profile

Cash Outflow year - $20,000

Cash Inflow

• 1st Year - $4000
• 2nd Year - $14,000
• 3rd Year - $22,000

The objective here is to find out whether you will accept this project or reject this project given a series of Cost of Capital or Discount Rates.

Using NPV

The cost of Capital is in the leftmost column starting from 0% and goes to 110% with a step of 10%.

We will accept the project if NPV is greater than 0, else we reject the project.

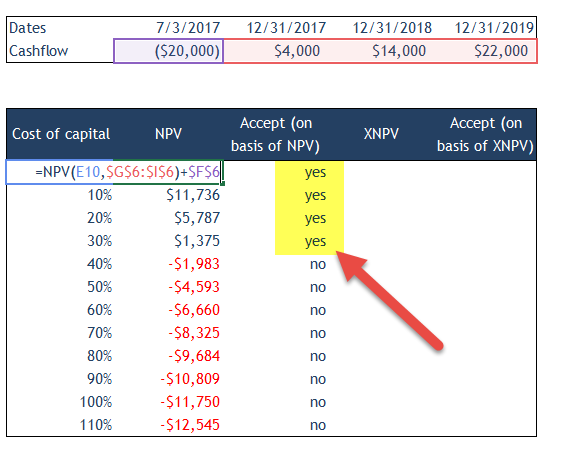
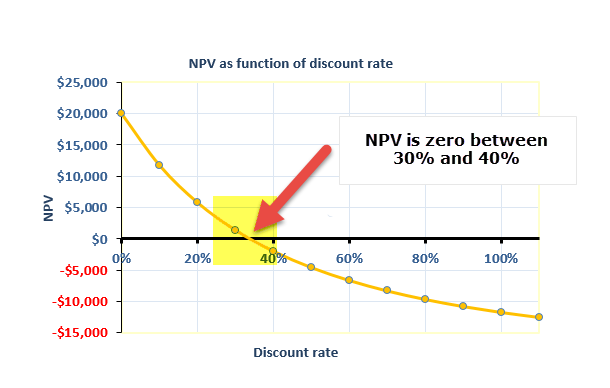
We note from the above graph that NPV is positive when the Cost of Capital is 0%, 10%, 20%, and 30%. This means that we accept the Project when the Cost of Capital is from 0% to 30%.

However, when the cost of Capital increases to 40%, we note that the Net Present value is negative. There we reject this project. We note that as the Cost of Capital increases, Net Present value decreases.

This can be seen graphically in the graph below.

Using XNPV

Let us now run the same example with the XNPV formula.

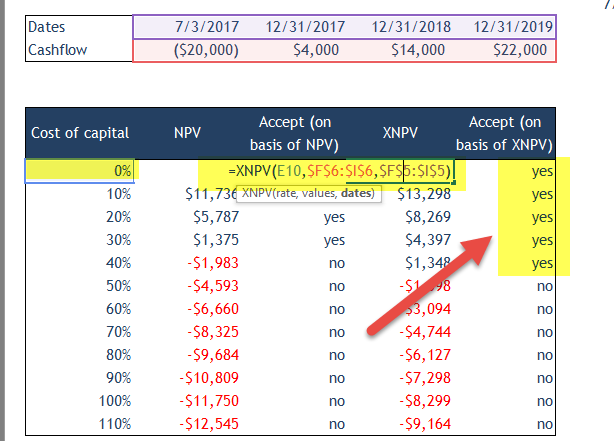
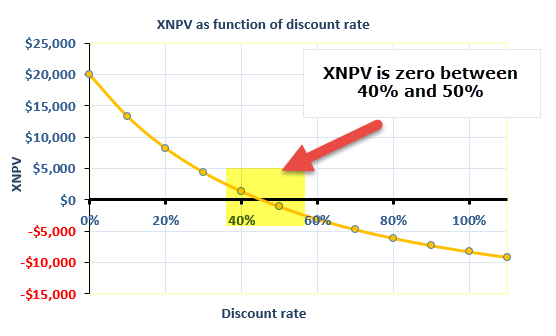
We note that Net Present Value is positive using XNPV for the cost of capital of 0%, 10%, 20%, 30% as well as 40%. This means that we accept the project when the cost of capital is between 0% and 40%. Please note that this answer is different from the one that we got using NPV, where we rejected the project when the cost of capital reached 40%.

The below graph depicts the Net Present Value of the Project using XNPV at the various cost of capital.

If the user gets an error while using the XNPV function in excel, this could fall in either of the below-mentioned categories:

This has been a guide to NPV vs XNPV. Here we discuss the top difference between NPV and XNPV along with excel calculation, examples, common errors. You may also have a look at the following articles –

• PV Function in Excel
• Examples of NPV
• Financial Distress Meaning
• Financial Modeling for Startups