Crossover Rate

What Is Crossover Rate?

The crossover rate is the intersection between the rate of return of two different projects having equal net present value (NPV). The calculation and visualization of two different rates of return of the two projects allow an investor or business to recognize cash flow trends and patterns and plan their capital expenditure accordingly.

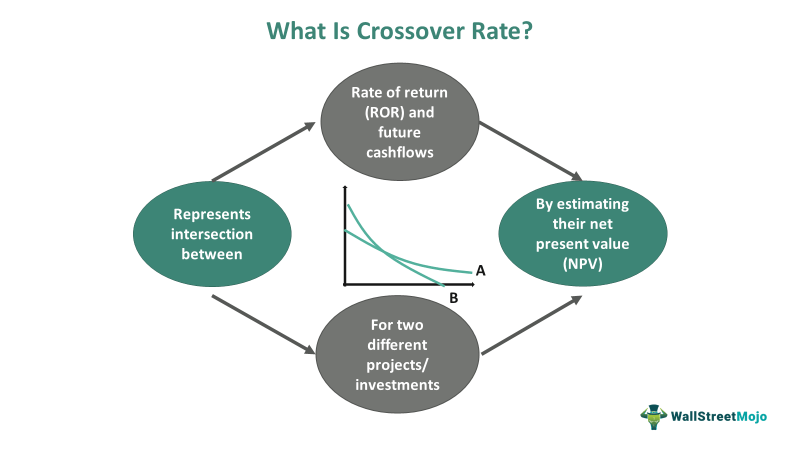
The crossover rate allows an investor or business to weigh their average returns against any costs incurred or capital invested in two different projects or financial instruments. Visualizing this rate allows entities to plan their capital expenditure and budget to ensure that one of the investments yields sufficient returns at any point.

• A crossover rate explains the net present value of two projects or investments determinable by their equal initial cost or present value of future cash flows. 
• Estimating the present value of future cash flows allows investors or businesses to understand the trends and patterns of crossovers between cash flows over the lifespan of two projects. 
• Such trends indicate when one project becomes superior to the other and worthier for future investments. 
• Thus, to plan healthier capital budgets and expenditures, the determination of crossover between annual cash flows, net present value, and internal rate of returns becomes necessary.

Crossover Rate Explained

The crossover rate, also can be understood as the weighted average cost of capital (WACC), is useful in comparing two projects with equal net present value (NPV) but with changing returns over time. The equal net present value (NPV) indicates that the cost and the present value of estimated future cash flows of the two projects for an investor or business are the same. Therefore, investors must evaluate the patterns or trends in their rate of return.

Suppose a company is planning investment into two projects of similar nature and equal cost – Project A and Project B. Although the cost incurred by the company on its two projects is the same, due to various differentiating characteristics like location, season, customer preferences, etc., the returns or profits generated from the two projects keep changing.

Additionally, the difference between the two curves showing the net present value (NPVs) reveals when one project yields higher gains than the other. Similarly, crossovers are useful in the technical analysis of the exchange rate of two currencies over time. These exchange rate crossovers allow investors, traders, and businesses to predict growth cycles or lower returns by comparing a pair of currencies and their exchange rates over time.

Additionally, an investor shall use a crossover rate to compare the return on investments for two different securities over time. The estimation and calculation of crossovers allow the investor to become sure of profitability. Additionally, it assists in predicting the possibility of equal cashflows or returns from the two securities.  

Formula

Let us now look at the formula and understand how to compare the cash flows yielded by two projects with the same initial net present value (NPV). Although the crossovers between NPV for any two assets, projects or securities are comparable by their cash flow streams over time, initial costs or investments, or the expected annual rate of return.

To derive the formula, let the two projects be – Project A and Project B,

Project A has an initial investment worth X, and it will generate cash flows for four years. Thereby, it generates cash flows annually for four years, represented by CF(I), CF(II), CF(III), and CF(IV), respectively. Hence, the net present value (NPV) of Project A is,

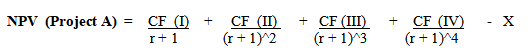
Whereas Project B has an initial investment worth Y, and it will generate cash flows for three years. Thus, the project generates cash flows annually for three years, represented by BCF (I), BCF (II), and BCF (III). Hence, the net present value of Project B is,

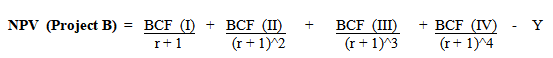
Thus, the crossover rate is the rate of return at which the NPV (Project A) = NPV (Project B). Therefore, as the value for CF (I), CF (II), CF (III), CF (IV), BCF (I), BCF (II), and BCF (III) are known, the crossover rate is determinable by solving for two equations.

How To Calculate?

The crossover rate calculator or formula to determine the two net present values (NPVs) is determinable by equating actual or estimated cash flows from the two projects annually. However, other alternative methods to compare or find crossover rate include,

1. Equating the NPV in the above formula by 0. Thus, equating the NPV of a project with zero reflects that difference between annual cash flows or returns is zero.
2. Find the differences between the upfront or initial investments of the two projects,
3. Finding the cash flow streams for the two projects in the entire lifetime of a project generating cash flows. Thus, as the project ends or investment securities mature, it stops yielding cash flows in the succeeding years.
4. Determining the difference between the cash flows from two projects from different periods may have an equal initial investment.
5. Solving the above equation to determine the value of ‘r.’ 

Crossover Rate And IRR

Let us now compare and contrast the crossover rate and IRR to understand how investors or companies plan out their capital expenditures,

Crossover Rate	Internal Rate of Return (IRR)
It represents the intersection or (NPVs) of two projects that may have an equal initial investment.	It is a discount rate used to determine the expected annual rate of returns and profits from potential investment.
The calculation of the NPV crossover rate for the two projects is determinable using the cash flows generated from the project over time.	Its calculation is similar to that of determining NPV. However, the NPV is equal to zero. Therefore, the difference between the total cash flows and the initial cost will be zero.
The higher crossovers between the two projects reflect an inflow of equal cash flows from two projects with an equal initial investment.	The higher the internal rate of return, the higher the probability that an investor or company shall invest in a project.
Equal NPVs for two projects or intersections in the present value of future returns over their lifetime generating cash flows indicates a good capital investment.	Similarly, if the internal rate of return is equal to the cost of capital for a project, then it indicates a good investment. Thus, the discount rate in such a scenario is favorable.
The crossovers in NPVs indicate a healthy capital budget investment and planning. The analysis of the crossover rate will also indicate when the present value of future cash flows from one project becomes superior to the other due to various factors.	Although, there may be other quantitative and qualitative factors that assist in decision-making to go ahead with an investment. Cumulatively, an investment may be a failure wherein the IRR is lower than the minimum acceptable rate of return.

Frequently Asked Questions (FAQs)

Recommended Articles

This article has been a guide to What is Crossover Rate. Here, we explain its formula and calculation and compare it with IRR. You can also go through our recommended articles on corporate finance –

• NPV Profile
• NPV in Excel
• NPV vs XNPV